Прямая и обратная: Прямая и обратная пропорциональность. Формулы, обозначение, примеры

Содержание

Прямая и обратная пропорциональность. Формулы, обозначение, примеры

Основные определения

Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

Виды зависимостей:

Прямая зависимость. Чем больше одна величина, тем больше вторая. Чем меньше одна величина, тем меньше вторая величина.
Обратная зависимость. Чем больше одна величина, тем меньше вторая. Чем меньше одна величина, тем больше вторая.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.

Проще говоря — это зависимость одного числа от другого.

Есть две разновидности пропорциональностей:

Прямая пропорциональность. Это зависимость, при которой увеличение одного числа ведет к увеличению другого во столько же раз. А уменьшение одного числа ведет к уменьшению другого во столько же раз.
Обратная пропорциональность. Это зависимость, при которой уменьшение одного числа ведет к увеличению другого во столько же раз. А увеличение числа наоборот ведет к уменьшению другого во столько же раз.

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

a и d называются крайними членами, b и c — средними.

Основное свойство пропорции

Произведение крайних членов равно произведению средних членов.

Свойство прямо пропорциональной зависимости:

Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Примеры прямо пропорциональной зависимости:

при постоянной скорости пройденный маршрут прямо-пропорционально зависит от времени;
периметр квадрата и его сторона — прямо-пропорциональные величины;
стоимость конфет, купленных по одной цене, прямо-пропорционально зависит от их количества.

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров».

Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

Формула прямой пропорциональности

y = kx,

где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

y/x = k

Пример 1.

В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

Как решаем:

Вспомним формулу для определения пути через скорость и время: S = V * t.

Так как оба автомобиля проделали одинаковый путь, можно составить пропорцию из двух выражений: 70 * 2 = V * 7

Найдем скорость второго автомобиля: V = 70 * 2/7 = 20

Ответ: 20 км/ч.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Пример 2.

Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?

Как рассуждаем:

Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.

Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:

х = 1 (блогер) * 30 (раз) : 12/8 (дней).
х = 1 * 30 : 12/8
х = 20

Ответ: 20 человек напишут 420 постов за 12 дней.

Обратно пропорциональные величины

Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

Свойство обратной пропорциональности величин:

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины;
при одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи;
количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене.

Формула обратной пропорциональности

y = k/x

где y и x — это переменные величины,

k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

xy = k.

Потренируемся

Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Как рассуждаем:

В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.

Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

Как решаем:

Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию: 30 : 24 = 5 : х

Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член: х = 24 * 5 : 30; х = 4

Значит, 30 человек раскрутят канал за 4 дня.

Ответ: за 4 дня.

Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Как рассуждаем:

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Обозначим:

v1 = 75 км/ч

v2 = 52 км/ч

t1 = 13 ч

t2 = х

Как решаем:

Составим пропорцию: v1/v2 = t2/t1.
Соотношения равны, но перевернуты относительно друг друга.

Подставим известные значения: 75/52 = t2/13

Ответ: 18 часов 45 минут.

Урок 7. прямая и обратная пропорциональность. решение задач — Математика — 6 класс

Математика

6 класс

Урок № 7

Прямая и обратная пропорциональность. Решение задач

Перечень рассматриваемых вопросов:

Понятия прямой и обратной пропорциональной зависимости.
Краткая запись условия задачи.
Составление и решение пропорций по условию задачи.
Решение задач на прямую и обратную пропорциональную зависимость.

Тезаурус

Равенство двух отношений называют пропорцией.

Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.

Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.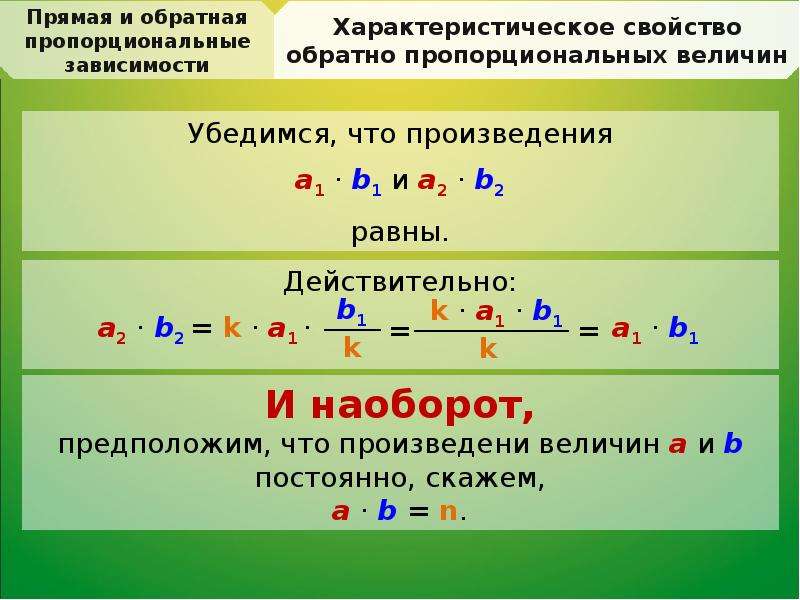

Основная литература

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Прямая пропорциональность.

Обратная пропорциональность.

Для решения задач на пропорциональную зависимость, удобно составить таблицу или сделать краткую запись условия.

Столбцы таблицы соответствуют наименованиям зависимых величин.

Строки таблицы соответствуют значениям величин при первом и втором измерении.

Одинаково направленные стрелки показывают прямо пропорциональную зависимость, противоположно направленные – обратно пропорциональную.

Задача.

Поезд, скорость которого 55 км/ч, был в пути 5 часов. За сколько часов пройдёт этот же участок пути товарный поезд, скорость которого 45 км/ч?

Решение.

При постоянном пути скорость и время движения обратно пропорциональны.

Допустим, товарный поезд пройдёт этот же путь со скоростью 45 км/ч за x ч.

Сделаем краткую запись условия.

Задача.

Двигаясь с постоянной скоростью, велогонщик проезжает 40 метров за 3 с. Какой путь проедет велогонщик за 45 с?

Решение.

При постоянной скорости путь прямо пропорционален времени движения.

Пусть х м проедет велогонщик за 45 с.

Сделаем краткую запись условия.

Задача.

Усилие при восхождении на высоту 600 м равно усилию, требуемому для перехода 25 км по равнине. Турист поднялся в горы на 792 м. Какому расстоянию на равнине соответствует этот подъём?

Решение:

Решение.

Задача.

Четыре программиста могут написать игру за 12 месяцев. За сколько месяцев эту работу могут выполнить три программиста?

Решение.

Количество программистов и скорость написания игры – это обратно пропорциональная зависимость.

Разбор заданий тренировочного модуля

№ 1. Подстановка элементов в пропуски в тексте.

Подставьте нужные элементы в пропуски.

Пешеход шёл 3 часа со скоростью 8 км/ч. За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?

Решение:

При фиксированном расстоянии время в пути и скорость – ______ пропорциональны.

Пусть _____ часов – пешеход идёт со скоростью 6 км/ч.

Составим пропорцию:

_________

х=_______

х=_______(ч).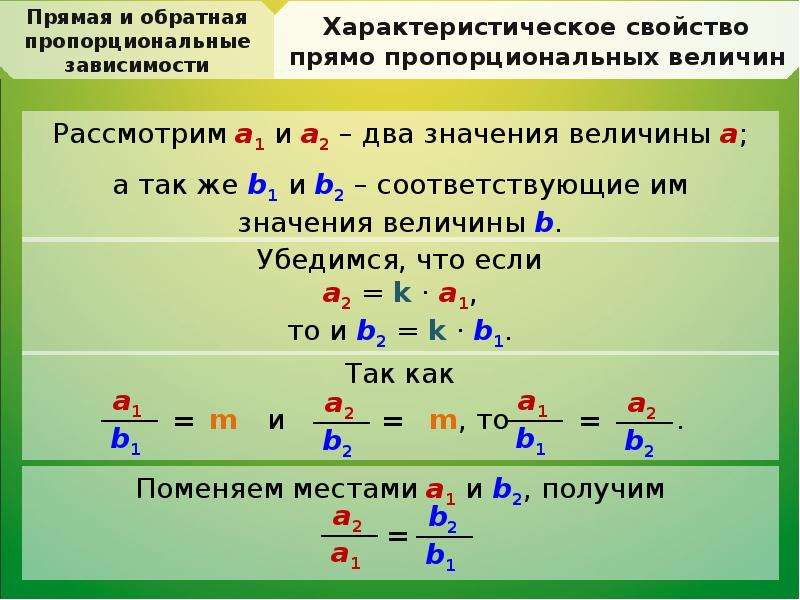

Правильный ответ.

Решение:

При фиксированном расстоянии время в пути и скорость – обратно пропорциональны.

Пусть х часов – пешеход идёт со скоростью 6 км/ч.

№ 2. Подстановка элементов в пропуски в таблице.

Заполните таблицу.

Поезд движется со скоростью 45 км/ч. Какое расстояние он пройдёт, если будет в пути 3 ч; 4 ч; 5 ч; 6 ч.

Варианты ответов:

135 км;

180 км;

225 км;

270 км.

Решение.

При постоянной скорости пройденный путь и время прямо пропорциональны. Скорость движения поезда 45 км/ч означает, что за 1 час поезд преодолевает расстояние в 45 км. Обозначим за x км – расстояние, которое поезд пройдёт за 3, 4, 5 и 6 часов.

Таким же способом находим расстояние, которое пройдёт поезд за 4, 5 и 6 часов, и подставляем соответствующие варианты в таблицу.

Ответ:

Прямая и обратная пропорциональная зависимость — Kid-mama

Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.

Проще всего понять прямо пропорциональную зависимость на примере станка, изготавливающего детали с постоянной скоростью. Если за два часа он делает 25 деталей, то за 4 часа он изготовит деталей вдвое больше — 50. Во сколько раз дольше времени он будет работать, во столько же раз больше деталей он изготовит.

Математически это выглядит так:

4 : 2 = 50 : 25 или так: 2 : 4 = 25 : 50

Прямо пропорциональными величинами тут являются время работы станка и число изготовленных деталей.

Говорят: Число деталей прямо пропорционально времени работы станка.

Если две величины прямо пропорциональны, то отношения соответствующих величин равны. (В нашем примере — это отношение времени 1 к времени 2 = отношению количества деталей за время 1 к количеству деталей за время 2)

Обратная пропорциональность

Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.

Обратно пропорциональная зависимость часто встречается в задачах на скорость. Скорость и время являются обратно пропорциональными величинами. Действительно, чем быстрее движется объект, тем меньше времени у него уйдет на путь.

Например:

Если величины обратно пропорциональны, то отношение значений одной величины (скорости в нашем примере) равно обратному отношению другой величины ( времени в нашем примере). ( В нашем примере — отношение первой скорости к второй скорости равно отношению второго времени к первому времени.

Задача 1:

Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?

Решение:

Запишем краткое условие задачи:

Задача 2:

Для перевозки груза потребовалось 24 машины грузоподъемностью 7,5 тонн. Сколько нужно машин грузоподъемностью 4,5 т, чтобы перевезти тот же груз?

Решение:

Краткая запись:

Градштейн И.

С. Прямая и обратная теоремы. — 1959 // Библиотека Mathedu.Ru
Градштейн И. С. Прямая и обратная теоремы. — 1959
Подготовка
текстаПодготовка
текста
Содержание
Загрузка
структуры
Информация
Загрузка
описаний
Справка
Загрузка
справки
Поиск
Страниц найдено: 1
Если строка в кавычках «…», то найдутся страницы со словосочетанием в точно такой форме.
Если слова указаны через пробел или оператор «&», то найдутся страницы, содержащие все введенные слова в одном предложении.
Если указано несколько слов через оператор «|», то найдутся страницы, содержащие любое из введенных слов.
Если указано два слова через оператор «~», то найдутся страницы, содержащие первое, но не содержащие второе слово в одном предложении.
По вашему запросу ничего не найдено.
Убедитесь, что слова написаны без ошибок или попробуйте выбрать другие значения.
null
Подождите,
пожалуйста…
Печать
Обложка123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128
Подготовка [0%]…
Отмена
{«root»:»text»,»url»:»gradshteyn_pryamaya_i_obratnaya_teoremy_1959″,»surl-package»:»\/text\/%PACKAGE%\/?query=%QUERY%»,»surl-page»:»\/text\/%PACKAGE%\/p%PAGE%\/?query=%QUERY%»,»query»:»\»\»»,»section»:»library»,»mode-gfx»:true,»mode-html»:true,»mode-prefer»:»gfx»,»layout-prefer»:»1×1″,»zoom»:{«1×1»:{«level»:100,»_w»:false,»_h»:true},»2×1″:{«level»:100,»_w»:true,»_h»:false},»html»:{«level»:100}},»textsize-prefer»:»2″,»textfont-prefer»:»a»,»tree-type»:»ajax»,»tree-state»:»visible»,»printbox-state»:»hidden»,»print-allowed»:»1″,»searchbox-state»:»hidden»,»searchbox-type»:»inline»,»goto-pageno»:null,»goto-page»:-1,»defw»:»1000″,»defh»:»1612″,»minh»:1612,»maxh»:1612,»fixeven»:null,»package»:»left»,»sitemode»:»live»,»user»:{«uuid»:»»}}
Удерживайте правую кнопку мыши для выделения группы страниц.
Удерживайте клавишу Shift для выделения диапазона страниц.
Удерживайте клавишу Ctrl для перехода к странице без её выделения.
Позволяет находить заданные слова и словосочетания в тексте публикации.
Поиск поддерживает кириллический и латинский алфавиты.
Переключайте вид списка результатов поиска кнопками «Список» и «Карта».
Функция печати/скачивания доступна только зарегистрированным пользователям.
Пожалуйста, зарегистрируйтесь или авторизуйтесь.
Выбор оформления (светлое/тёмное) доступен только зарегистрированным пользователям.
Пожалуйста, зарегистрируйтесь или авторизуйтесь.
Прямая и обратная пропорциональные зависимости
Сегодня на уроке мы продолжим работать с пропорциями, а точнее познакомимся с прямой и обратной пропорциональными зависимостями.
Задача
Сколько нужно сахара, чтобы сварить варенье из 5 кг черешни, если по рецепту на 2 кг ягод нужно 3 кг сахара?
Решение:
Из решения видно, что во сколько раз больше имеется черешни, во столько раз больше понадобится сахара.
Эту же задачу можно решить и при помощи пропорции. Запишем кратко условие задачи в виде таблицы, обозначив за неизвестную нам массу сахара буквой х. Смотрите, у нас есть столбик, где мы будем записывать массу ягод, и столбик, где мы укажем соответствующую массу сахара на массу ягод. Итак, по условию задачи известно, что по рецепту на 2 кг ягод нужно 3 кг сахара. Нам нужно узнать, сколько кг сахара потребуется на 5 кг ягод.
Такая зависимость между массой ягод и массой сахара условно обозначается в таблице одинаково направленными стрелками. Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то и вторая тоже возрастает (стрелка тоже вверх).
Задача
Велосипедист, двигаясь с постоянной скоростью, проехал 10 км за 20 минут. Какой путь проедет велосипедист за 50 минут?
Решение: для наглядности запишем кратко условие задачи в виде таблицы.
Понятно, что путь увеличится во столько раз, во сколько раз увеличится время. Ставим стрелки в одном направлении.
Такие величины, как масса ягод для варенья и масса сахара, время и пройденный за это время при постоянной скорости путь, и т.д. называют прямо пропорциональными величинами.
Определение
Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Задача
Автомобиль ехал 3 часа со скоростью 60 км/ч. За какое время он продет это же расстояние, если будет ехать со скоростью 90 км/ч?
Решение:
Из решения видно, что во сколько раз скорость автомобиля больше, во столько раз меньше времени тратится на этот же путь.
Эту же задачу решим при помощи пропорции. Запишем в таблицу кратко условие задачи. За х обозначим неизвестное нам время.
Понятно, что чем больше скорость автомобиля, тем меньше времени ему понадобится на преодоление этого же пути. Такая зависимость между скоростью и временем, затраченным на пройденный путь, условно обозначается в таблице противоположно направленными стрелками. Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то вторая убывает (стрелка вниз). Составим пропорцию. Т.к. стрелки направлены в разные стороны, то второе отношение перевернём.
Задача
5 рабочих выполнили заказ за 132 часа. За какое время этот же заказ смогут выполнить 12 рабочих?
Решение:
Понятно, что чем больше будет задействовано рабочих, тем быстрее выполнится заказ. Значит, ставим стрелки в противоположном направлении.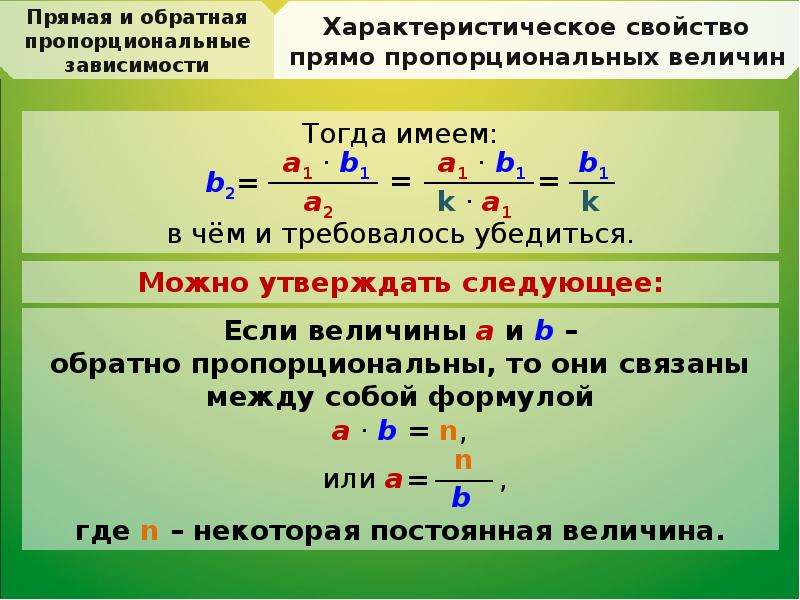 Составим пропорцию:
Такие величины, как скорость автомобиля и время, за которое он проедет определённый путь, число работников и время, за которое они выполняют заказ, и т.д. называют обратно пропорциональными величинами.
Определение
Две величины называются обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
Не всякие две величины являются прямо пропорциональными или обратно пропорциональными.
Например, возраст человека и размер его обуви не связаны пропорциональной зависимостью. Зависимость между величинами есть. Размер обуви с возрастом увеличивается, но не во столько же раз.
Возраст дерева и его высота не связаны пропорциональной зависимостью. В этом случае зависимость между величинами есть. Действительно, высота дерева с возрастом увеличивается, но не во столько же раз.

Глава 3. Прямая и обратная пропорциональность
Ниже приведены некоторые задачи, которые легко решаются с использованием свойств прямой и обратной пропорциональности.

Задача
Вор угнал машину в городе А и отправился в город В со скоростью 60 км/ч. Расстояние между городами 400 км. Через 30 мин после угона полицейский из города А стал преследовать вора со скоростью 80 км/ч. Через сколько километров полицейский догнал вора?
Задача
Из-за ремонта на железнодорожных путях поезд вынужден ехать со скоростью, равной ¾ от его обычной скорости. Из-за этого из пункта А в пункт В он придет позже на 20 минут. Найдите время, за которое обычно поезд проезжает расстояние от пункта А до пункта В.

Задача
Из пункта А в пункт В выехали два велосипедиста. Скорость одного – 6 км/ч, а скорость другого 10 км/ч.
Если один из них на дорогу тратит на 30 минут больше, чем другой, то какое расстояние от пункта А до пункта В?

Задача
В гонке на 200 метров А побеждает В на 20 метров, а С побеждает на 40 метров. Если В и С бегут с теми же скоростями на 100 метров, то насколько метров В победит С?

Задача
Путешествие длиной 192 км на скоростном поезде занимает на 2 часа меньше, чем на электричке. Скорость электрички на 16 км/ч меньше, чем у скорого поезда. Какая скорость у скорого поезда?

Задача
Соня и Аня учувствуют в 100 метровой гонке. Соня пробегает 100 метров за 20 секунд, а Аня за 25 секунд. На сколько метров отстает Аня от Сони, когда Соня прибегает к финишу?

Задача
Соня возвращалась домой со скоростью, равной ¾ от ее обычной скорости и пришла домой на 25 минут позже обычного. Сколько времени у нее обычно занимает эта дорога?
Презентация «Прямая и обратная пропорциональность»
библиотека
материалов
Содержание слайдов
Номер слайда 1
№ 53 (а, б), 54 (а, б),57.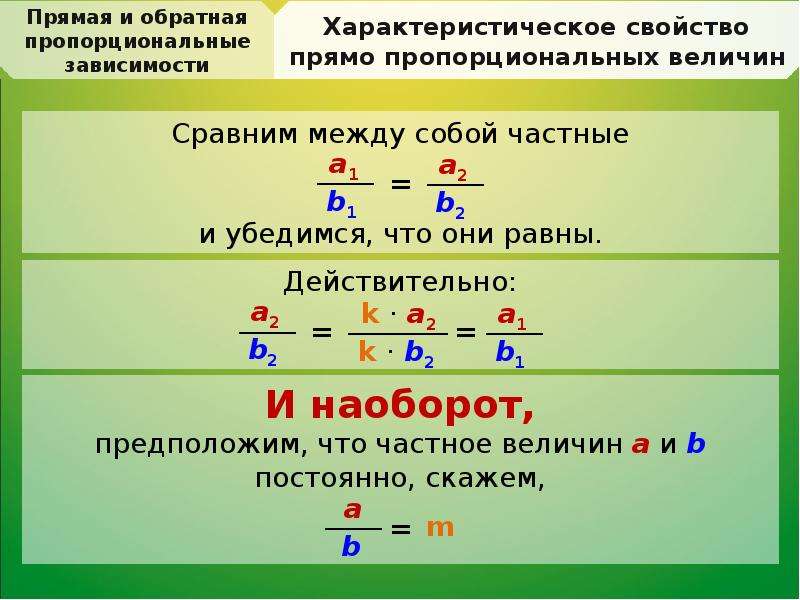 Проверка домашней работы:
Номер слайда 2
№ 53 (а, б)а) х=𝟐·𝟑𝟕, х=𝟔𝟕. б) х=𝟐·𝟑𝟓, х=𝟔𝟓.
Номер слайда 3
№ 54 (а, б)а) х=𝟕·𝟔𝟖, х=𝟐𝟏𝟒. б) х=𝟏𝟎·𝟏𝟑𝟏𝟓, х=𝟐𝟔𝟑.
Номер слайда 4
№ 57а) х=𝟏𝟐·𝟑𝟓, х=𝟑𝟏𝟎. б) х=𝟐𝟑·𝟑𝟒, х=𝟏𝟐.
Номер слайда 5
№ 57в) х=𝟓·𝟕𝟏𝟐, х=𝟕𝟎. г) х=𝟏𝟑·𝟔𝟖, х=𝟏𝟒.
Номер слайда 6
Математический диктант: Верно ли, что:1) Отношение двух чисел — это произведение одного из них на другое?2)Верное равенство двух отношений называют пропорцией?3)Произведение крайних членов пропорции равно сумме её средних членов? 4)Найти неизвестный член пропорции – это значит решить пропорцию?618.09.2019
Номер слайда 7
Верно ли, что:5)В пропорции m:n=p:q числа m и q называют средними, а числа n и p называют крайними членами пропорции?6)Является пропорцией данное равенство: 8:10=4:5?7)Можно составить пропорцию из чисел 4, 9, 12 и 27?8)Пройденный путь пропорционален времени движения когда скорость постоянна?9)Рост человека пропорционален его возрасту? Математический диктант:
Номер слайда 8
Проверь себя : 1 2 3 4 5 6 7 8 9- + — + — + + + -89 правильных ответов – «5»7 – 8 правильных ответов – «4»4 – 5 правильных ответов – «3»
Номер слайда 9
Устно: Что называется отношением двух чисел?Что называется отношением двух величин?Что такое пропорция?Что показывает отношение двух чисел? Что значит решить пропорцию?Основное свойство пропорции.
Номер слайда 10
1. Если нам известно,что скорость автомобиля составляет 60 км/ч,то мы можем рассчитать пройденноеим расстояние за любой отрезок времени:{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60120{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60120180{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60120180240{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60120180240300{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60120180240300360 Какой вывод можно сделать по данным этой таблицы?Если время увеличить (уменьшить)в некоторое число раз,то и расстояние увеличится (уменьшится)в это же число раз.
Номер слайда 11
2. На 120 р. необходимо купить несколько одинаковых книг. Сколько книг можно купить, если цена каждой 10 р., 20 р., 30 р., 40 р.?Решение: С=10 р., к=12 книг;С=20 р., к=6 книг;С=30 р., к=4 книги;С=40 р., к=3 книги. Какой вывод можно сделать из данного решения?Если стоимость увеличить (уменьшить)в некоторое число раз,то и количество книг уменьшится (увеличится) в это же число раз.
Номер слайда 12
Прямая и обратная пропорциональность18. 09.2019«Всякая задача кажется очень простой, после того, как вам ее растолкуют» Шерлок Холмс.
Номер слайда 13
Цель урока:ввести новые понятия прямой и обратной пропорциональных зависимостей; научиться решать задачи, с использованием прямой и обратной пропорциональными зависимостями.
Номер слайда 14
Определение прямой и обратной пропорциональности. Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается(уменьшается) во столько же раз. Вел. 1 — Вел 2 Вел 1. — Вел 2. Вел. 1 — Вел 2 Вел 1. — Вел 2.
Номер слайда 15
Определение прямой и обратной пропорциональности. Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз. Вел. 1 — Вел 2 Вел 1. — Вел 2.
Номер слайда 16
Работа по учебнику: стр.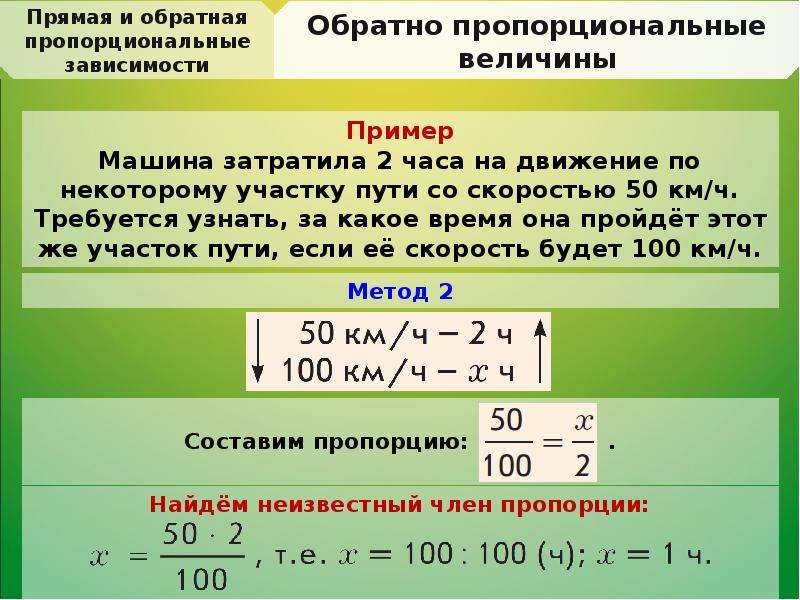 21№72 Время Расстояние Пусть x км расстояние. 6 ч 480 км 2 ч x км. Решение: x = x = 160 (км) Ответ: 160 км. =
Номер слайда 17
Работа по учебнику: стр. 22№82(а) Время Скорость Пусть x ч время. 8 ч 60 км/ч x ч 80 км/ч. Решение:=x =X = 6 (ч) Ответ: 6 ч.
Номер слайда 18
Алгоритм решения задач:1. Записать краткое условие задачи. (одноименные величины ставятся одна под другой).2. Определить к какому виду относится пропорция.3. Составить пропорцию.3а) При прямой пропорциональности, величины записываются не меняя порядка.3б) При обратной пропорциональности, величины меняют местами (у одной величины).4. Найти неизвестный член пропорции.5. Ответить на вопрос задачи.6. Записать ответ.
Номер слайда 19
Учебник: стр. 20№62, 63, 65. Устно:
Номер слайда 20
Работа в парах:№74 Вишня Сахарный Пусть x кг масса вишни. песок 6кг 4 кг x кг 12 кг = x = x = 18 (кг). Ответ: 18 кг.
Номер слайда 21
Работа в парах№77(а)Количество Количество Пусть x дней работа маляров дней 10 маляров. 5 8 10 x = x = x = 4 (дн). Ответ: 4 дня.
Номер слайда 22
Рефлексия. Урок понравился, я работал (ла) активно, отвечал (ла) на все вопросы правильно. Остались вопросы, я стеснялся (ась) отвечать на уроке, был (а) не уверен (а) в ответе. Урок не понравился, было много не понятного.
Номер слайда 23
Домашнее задание:1)п.1.5 (правила), №74, №76.2)Дополнительное задание: №79, №80.3)Творческое задание: Найдите в учебнике, справочной литературе или Интернете, как решали задачи на прямую и обратную пропорциональности во времена Л. Ф. Магницкого. Придумайте задачу и решите её этим способом.
Номер слайда 24
Вы можете использовать данное оформление для создания своих презентаций, но в своей презентации вы должны указать источник шаблона: Ранько Елена Алексеевна учитель начальных классов МАОУ лицей №21 г. Иваново. Сайт: http://elenaranko.ucoz.ru/
Номер слайда 25
Интернет – ресурсы:http://www.mamusik.ru//upload/userimages/kpwoktwyzvbpodhaalxho.jpeg фонhttp://s1.pic4you.ru/allimage/y2012/10-26/12216/2601759.png книгиhttp://mosaica.ru/sites/default/files/news/preview/2009/07/27/1_sent.jpg колокольчикhttp://img-fotki.yandex.ru/get/6409/131624064.235/0_906e7_8c51635e_XLосенний букетhttp://s3.uploads.ru/5o8gm.pngрамка
Как работают контуры регулирующих клапанов прямого и обратного действия ~ Изучение приборостроения и техники управления
Типовой контур регулирующего клапана состоит из четырех основных элементов:
(a) Контролируемый процесс, в основном приложения для потока или давления
(b) Контроллер процесса, который инициирует управляющее воздействие на регулирующий клапан
(c) Позиционер клапана (почти всегда требуется в большинстве приложений)
Эти основные элементы работают согласованно, чтобы обеспечить желаемый результат контроля. Контуры регулирующих клапанов могут работать в двух основных режимах:
(a) Петли прямого действия
(b) Петли обратного действия
Петли регулирующего клапана прямого действия :
В показанном ниже контуре регулирующего клапана прямого действия:
Контур регулирующего клапана прямого действия
Контроллер, позиционер и регулирующий клапан, действующие следующим образом:
(a) Действие контроллера :
Когда переменная процесса (расход или давление) увеличивается численно, выходной сигнал контроллера увеличивается пропорционально, и наоборот
(b) Действие позиционера клапана :
По мере увеличения входного сигнала на позиционер клапана от контроллера увеличивается выходная нагрузка или давление воздуха от позиционера
(c) Действие регулирующего клапана :
Когда давление воздуха или нагрузка на привод клапана увеличиваются, плунжер клапана перемещается в положение закрытия для клапана с режимом ATC – FO (воздух-закрытие, открытие при отказе).
Петли регулирующего клапана обратного действия :
В показанном ниже контуре регулирующего клапана обратного действия:
Контур регулирующего клапана обратного действия
Контроллер, позиционер и регулирующий клапан действуют следующим образом:
(a) Действие контроллера :
Когда переменная процесса (расход или давление) увеличивается численно, выходной сигнал контроллера уменьшается пропорционально и наоборот
(b) Действие позиционера клапана :
По мере уменьшения входного сигнала на позиционер клапана от контроллера выходная нагрузка или давление воздуха от позиционера увеличиваются
(c) Действие регулирующего клапана
Когда давление воздуха или нагрузка на привод клапана увеличиваются, плунжер клапана перемещается в открытое положение для клапана с режимом ATO — FC (воздух открывает, закрывается при отказе).
Для различных применений регулирующих клапанов контроллер, позиционер и регулирующий клапан могут быть настроены на прямое или обратное или на прямое и обратное в одном и том же контуре управления в зависимости от требований различных приложений.
Контроллеры
: Прямое и…. — Химическое машиностроение. Вопросы и ответы.
Контроллеры
: Прямое и обратное управление. выход уменьшается, когда измерение повышается, это контроллер обратного действия.Кроме того, при минимальной мощности контроллера должно быть достигнуто желаемое безотказное действие. Например, если у нас есть два контроллера на дистилляционной колонне — рефлюкс и верхний погон, — где клапан управления обратным потоком открыт при отказе, а регулирующий клапан верхнего потока нетто
закрыт при отказе, то контроллер орошения будет обратного действия, и Регулятор сетевых накладных расходов будет прямого действия. В любом случае положение отказа и действия регулятора определяются самостоятельно, поэтому о них поговорим отдельно. Положение отказа клапана определяется соображениями безопасности. Если в случае неудачи вы хотите, чтобы ваша колонка работала с полным обратным холодильником, ваш выбор правильный (рис. 1). Предполагая, что приводы клапанов являются пневматическими с пружинным приводом (вы не сказали, какие они были), и предполагая, что вы определяете «отказ» как прекращение подачи воздуха, пружина будет действовать, открывая клапан с отказоустойчивым открытием (FO). и закрывать клапан с аварийным закрытием (FC), независимо от действий контроллера. (Я
не упоминаю роль позиционеров, потому что мне не нравится использовать их на клапанах управления потоком, потому что они могут быть медленнее, чем процесс потока, и, следовательно, они могут вызвать цикличность.)
Теперь обратимся к теме действия контроллера. Если предположить, что ваша система такая, как показано на рисунке, повышение температуры колонки должно привести к усилению охлаждения, что достигается за счет возврата большего количества холодного орошения в колонку. Это означает, что регулятор температуры (TC) должен уменьшить уставку потока флегмы, что, в свою очередь, повысит
уровень в накопителе, и для преодоления этого регулятор уровня (LC) увеличит уставку регулирования потока флегмы (FC). ).Таким образом, увеличение измерения требует, чтобы TC уменьшал свой выходной сигнал (обратное действие, R/A), в то время как LC увеличивает свой выходной сигнал при повышении уровня (D/A). Реакцией подчиненных контроллеров FC является увеличение расхода через их клапаны по мере того, как ведущий повышает свою уставку, поэтому с клапаном FC это будет D/A, а с клапаном FO
будет R/A.
Разработка количественной ПЦР с прямой обратной транскрипцией (dirRT-qPCR) для клинической диагностики вируса Зика
Цель: Анализ полимеразной цепной реакции (ПЦР) на основе нуклеиновых кислот обычно применяется для выявления заражения вирусом Зика (ZIKV). Однако длительная и трудоемкая предварительная обработка образцов, необходимая для удаления ингибиторов, вызывающих ложноотрицательные результаты в клинических образцах, нецелесообразна для использования в областях с ограниченными ресурсами. Цель состояла в том, чтобы разработать прямой количественный ПЦР с обратной транскрипцией (dirRT-qPCR) для диагностики ZIKV непосредственно из клинических образцов.
Методы: Комбинация устойчивых к ингибиторам полимераз, энхансеров полимеразы и условий dirRT-qPCR была оптимизирована для различных клинических образцов, включая кровь и сыворотку.Чувствительность оценивали с добавлением стандартной ДНК в смоделированные образцы. Специфичность оценивали с использованием клинических образцов других инфекций, таких как вирус денге и вирус чикунгунья.
Результаты: Были достигнуты высокая специфичность и чувствительность, а предел обнаружения (LOD) анализа составил 9,5×10 ¹ копий РНК ZIKV/реакцию. Для клинической диагностики ZIKV на месте требовался образец объемом 5 мкл, и диагностика могла быть завершена в течение 2 часов.
Выводы: Этот надежный анализ dirRT-qPCR показывает высокий потенциал для диагностики по месту оказания медицинской помощи, а комбинации праймер-зонд также могут быть расширены для обнаружения других вирусов. Он реализует цель крупномасштабного скрининга вирусных инфекций на местах и может использоваться для ранней диагностики, предотвращения и контроля вирусных вспышек.
Ключевые слова: Клиническая диагностика Зика; Прямое обнаружение образца; Молекулярная диагностика; dirRT-КПЦР.
Прямая и обратная перезапись в области взаимодействия данных
‘) var buybox = document. querySelector(«[data-id=id_»+ метка времени +»]»).parentNode ;[].slice.call(buybox.querySelectorAll(«.вариант-покупки»)).forEach(initCollapsibles) функция initCollapsibles(подписка, индекс) { var toggle = подписка.querySelector(«.Цена-варианта-покупки») подписка.classList.remove(«расширенный») var form = подписка.querySelector(«.форма-варианта-покупки») var priceInfo = подписка.querySelector(«.Информация о цене») var PurchaseOption = toggle.parentElement если (переключить && форма && priceInfo) { toggle.setAttribute(«роль», «кнопка») переключать.setAttribute(«табиндекс», «0») toggle.addEventListener («щелчок», функция (событие) { var expand = toggle.getAttribute(«aria-expanded») === «true» || ложный toggle. setAttribute(«aria-expanded», !expanded) form.hidden = расширенный если (! расширено) { покупкаOption.classList.add(«расширенный») } еще { покупкаВариант.classList.remove («расширенный») } priceInfo.hidden = расширенный }, ложный) } } функция initKeyControls() { document.addEventListener («нажатие клавиши», функция (событие) { if (document.activeElement.classList.contains(«цена-варианта-покупки») && (event.code === «Пробел» || event.code === «Enter»)) { если (документ.активный элемент) { событие.preventDefault() документ. activeElement.click() } } }, ложный) } функция InitialStateOpen() { вар buyboxWidth = buybox.offsetWidth ;[].slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) { var toggle = опция.querySelector(«.Цена-варианта-покупки») var form = option.querySelector(«.форма-варианта-покупки») var priceInfo = option.querySelector(«.Информация о цене») если (buyboxWidth > 480) { переключить.щелчок() } еще { если (индекс === 0) { переключить.щелчок() } еще { переключать.setAttribute («ария-расширенная», «ложь») form. hidden = «скрытый» priceInfo.hidden = «скрытый» } } }) } начальное состояниеОткрыть() если (window.buyboxInitialized) вернуть window.buyboxInitialized = истина initKeyControls() })()
Обратная ипотечная прямая почтовая рассылка ведет | Обратная ипотечная прямая почтовая рассылка ведет переводы в реальном времени | Обратная ипотечная прямая почтовая рассылка Call Transfers | Ведет в реальном времени
Обратная ипотечная прямая почтовая рассылка ведет | Обратная ипотечная прямая почтовая рассылка ведет переводы в реальном времени | Обратная ипотечная прямая почтовая рассылка Call Transfers | Лиды в реальном времени | Эксклюзивные лиды
Обратная ипотечная прямая почтовая рассылка
Прямой контакт с потенциальными заемщиками — лучший способ продать обратную ипотеку. Технологии Halbart делают это возможным для вас с помощью прямой почтовой рассылки по обратной ипотеке.
В США есть много пожилых домовладельцев, которые понятия не имеют о том, как они могут использовать свой собственный капитал, чтобы спокойно вести свою пенсионную жизнь. Те немногие, кто знает об обратной ипотеке, не могут выбрать ее из-за мифов, окружающих этот продукт. С помощью службы обратной почтовой рассылки по ипотеке мы рассылаем письма всем этим людям от вашего имени, чтобы они соответствовали требованиям ваших заемщиков
.
Как профессиональная компания, занимающаяся привлечением потенциальных клиентов, Halbart Technologies владеет полной базой данных пожилых домовладельцев, которые могут получить выгоду от обратной ипотеки.Отправляя письма этим потенциальным клиентам, мы гарантируем, что ваш почтовый ящик полон, а ваш телефон всегда звонит с вопросами от потенциальных клиентов, которые заинтересованы в получении обратной ипотеки. Самое приятное то, что вам не нужно ничего делать, кроме как предоставить нам свои спецификации о типах потенциальных клиентов, с которыми вы хотите, чтобы мы связались.
Команда Halbart Technologies состоит из экспертов по рассылке рекламных рассылок, направленных на улучшение бизнеса наших клиентов.Они точно знают, что нужно сделать, чтобы получить правильный ответ от ваших потенциальных клиентов. С помощью прямой почтовой рассылки обратной ипотеки мы позаботимся о том, чтобы ваши потенциальные клиенты были хорошо информированы о преимуществах получения обратной ипотеки, чтобы им было легко принять правильное решение. Все, что вам нужно будет сделать, это дать потенциальным клиентам ваши лучшие цитаты, когда они свяжутся с вами после получения этих рассылок.
Привлечение большего числа заемщиков по обратной ипотеке — единственный способ помочь вашему бизнесу по обратной ипотеке получить конкурентное преимущество в отрасли. Прямая почтовая рассылка по обратной ипотеке Halbart нацелена в первую очередь на эту цель. Мало того, что эта услуга будет очень выгодна для вашего обратного ипотечного бизнеса, она также будет очень доступной.
Итак, сообщите нам свои требования как можно скорее, позвонив нам по номеру
.
© 2015–2022 Halbart Technologies.Все права защищены.
Отмена прямого депозита
Узнайте, как запросить отмену прямого депозита, которая возвращает средства на ваш счет.
При расчете заработной платы вы можете запросить отмену прямого депозита в течение 5 рабочих дней с даты выплаты.
Обратите внимание, что за запрос на отмену взимается комиссия в размере 75 долларов США, даже если вы не получите деньги обратно.
Что нужно знать, прежде чем запрашивать возврат средств
Запросы на возврат средств не являются гарантией возврата средств.
Обработка транзакции реверсирования занимает 5 рабочих дней с даты запроса.
Прекращение выплаты не помешает зачислению заработной платы на банковский счет сотрудника или подрядчика. Это может привести к нехватке средств в Intuit.
Рекомендуется иметь обновленную форму разрешения на прямой депозит от всех ваших нынешних сотрудников и подрядчиков
Вам необходимо будет уведомить сотрудника или подрядчика о запросе на отмену.
Когда вы можете запросить отмену
Вы можете запросить отмену только в следующих случаях:
Общая сумма должна быть больше 50 долларов США (из-за комиссии за отмену прямого депозита в размере 75 долларов США
).
Вы можете сделать запрос между 3-м и 5-м днем после даты выплаты. Это делается для того, чтобы первоначальный чек не был отклонен. Если он отклонен, нет необходимости в отмене.
Банковский счет, с которого вы хотите снять средства, должен быть в профиле сотрудника.
Причина отмены — соответствие законам ACH или EFT. Например: повторяющиеся платежи или непреднамеренные платежи.
Как сделать запрос на отмену прямого перечисления заработной платы
Вы можете сделать запрос между 3-м и 5-м днем после даты выплаты. Чтобы начать запрос:
Откройте форму Direct Deposit Reversa l.
Выберите Новый запрос .
Заполните необходимую информацию и информацию о транзакции.
Выбрать Сохранить .
После того, как отмена будет одобрена (подробности см. в следующем разделе), вы можете аннулировать платежный чек в своих платежных ведомостях.
Что будет дальше
Ваш запрос будет рассмотрен, и вы получите уведомление, если он будет отклонен или принят.
Если чего-то не хватает, ваш запрос будет отправлен вам по электронной почте со списком необходимых исправлений. После того как вы сохраните изменения, мы снова рассмотрим запрос. Агент может связаться с вами, чтобы помочь вам в более сложных ситуациях.
Успешные развороты
Когда ваш запрос будет принят, вы получите электронное письмо с информацией о времени обработки и следующих шагах. Возврат может занять до 9 дней.
После того, как средства будут возвращены с банковского счета сотрудника или подрядчика, они будут зачислены на ваш банковский счет. Текущий баланс не может быть выплачен на вашем счете заработной платы. Процесс занимает до 14 дней.
Если аннулирование выполнено успешно или работник или подрядчик организует возврат чистой суммы, не забудьте аннулировать зарплату, что завершит аннулирование.
Споры и неудачные отмены
Если отмена прямого депозита не удалась, вы не можете аннулировать зарплату. Поскольку работник или подрядчик получил чистую заработную плату, валовая заработная плата является действительной. Единственный способ вернуть деньги — работать напрямую с сотрудником или подрядчиком.
Если вся сумма прямого депозита не доступна на банковском счете сотрудника или подрядчика, аннулирование будет отклонено, и средства не будут возвращены.
Сотрудник или подрядчик может оспорить отмену на срок до 60 дней.Если аннулирование оспаривается и средства были возвращены, Intuit оставляет за собой право дебетовать банковский счет вашей компании на оспариваемую сумму.
Регулирующие клапаны прямого действия и регулирующие клапаны обратного действия
Термины прямой и обратный часто используются при обсуждении регулирующих клапанов, позиционеров и контроллеров при написании историй управления для сложных контуров, хотя определения прямого и обратного кажутся довольно простыми.
Говорят, что прямое действие происходит, когда измеряемая переменная (также называемая переменной процесса PV) увеличивается, производство увеличивается. Когда измеряемая переменная увеличивается, противоположное действие называется снижением производства.
Регулирующий клапан — это клапан, который регулирует поток жидкости путем изменения размера проходного сечения в ответ на управляющий сигнал. Это позволяет напрямую контролировать скорость потока и, как следствие, параметры процесса, включая давление, температуру и уровень жидкости. На языке автоматического управления регулирующий клапан обозначается как исполнительный элемент .
Электрические, гидравлические или пневматические приводы обычно используются для открытия или закрытия автоматических регулирующих клапанов.Позиционеры клапана обычно используются с регулирующими клапанами, которые можно установить в любое положение между полностью открытым и полностью закрытым, чтобы обеспечить требуемую степень открытия клапана.
Клапаны с пневматическим приводом часто используются из-за их простоты, поскольку для них просто требуется сжатый воздух, тогда как для клапанов с электрическим приводом требуются дополнительные кабели и распределительное устройство, а для клапанов с гидравлическим приводом требуются линии подачи и возврата гидравлической жидкости высокого давления.
Традиционно сигналы пневматического управления основывались на диапазоне давления от 3 до 15 фунтов на кв.2-1,0 бар), или, в последнее время, электрический сигнал 4-20 мА для промышленных или 0-10 В для систем HVAC. Электрическое управление теперь часто включает сигнал связи Smart , наложенный на управляющий ток 4-20 мА, что позволяет передавать сигнал о состоянии и проверке положения клапана обратно на станцию управления.
Приводы
классифицируются как прямого действия или обратного действия , некоторые конфигурации показаны на схеме ниже.Повышенное пневматическое давление, подаваемое на диафрагму, поднимает шток клапана в приводе обратного действия (в клапане с нормальной посадкой это открывает клапан и называется воздухом для открытия ).
Увеличение пневматического давления, подаваемого на диафрагму, удлиняет шток клапана в приводе прямого действия (для клапана с обычным седлом это закрывает клапан и называется воздухом для закрытия ).
Факторы безопасности влияют на то, какое действие клапана используется.Когда пневматическая подача выходит из строя, может быть выгодно, чтобы клапан был полностью открыт. Это может быть c в другом приложении.
Li Ниже приведены три случая, сочетание которых приводит молодого инженера в замешательство.
Случай I: Состояние отказа регулирующего клапана, т.е. если происходит повреждение клапана, определяется как
Когда подача воздуха/питание/сигнал вызывает открытие клапана, говорят, что клапан находится в состоянии отказа фаллопиевых (FO) и если клапан определяется при потере подачи воздуха/ Если клапан закрыт из-за к питанию/сигналу, то говорят, что клапан находится в состоянии отказа при отказе-закрытии (FC).
Вариант II: Позиционер регулирующего клапана, который может быть настроен на прямое или обратное действие. Это зависит от выбранного вами типа привода клапана. Я не могу рассматривать это отдельно от Casie I. После того, как вы выбрали тип привода, вам нужно согласовать действие позиционера.
Вариант III: Контроллер может быть установлен как Прямой в РСУ/ПЛК, относящийся к контуру регулирующего клапана, или как работающий в обратном направлении. Я не вижу смысла в этом случае.
Почему мы говорим о контроллерах и регулирующих клапанах?
Автоматический регулирующий клапан состоит из трех основных секций, каждая из которых представлена в различных стилях и конструкциях:
Привод клапана, такой как шаровой или дроссельный клапан, перемещает регулирующий элемент клапана.
Позиционер клапана – Это устройство гарантирует, что клапан открыт до нужной степени. Проблемы трения и износа больше не являются проблемой.
Модулирующий элемент, плунжер и сферический шар входят в состав корпуса клапана.
В случае пневматического клапана возможны два альтернативных действия по управлению:
«Воздух или ток на открытие» – По мере увеличения значения управляющего сигнала ограничение потока уменьшается.
«Воздух или ток на закрытие» — при увеличении значения управляющего сигнала увеличивается ограничение потока.
Также возможен отказ режимов безопасности:
Отказ подачи воздуха или управляющего сигнала на закрытие «- Если в приводе отсутствует сжатый воздух, клапан закрывается под давлением пружины или с резервным питанием.
Сбой подачи воздуха или управляющего сигнала на открытие «- Если привод теряет сжатый воздух, клапан открывается под давлением пружины или с резервным питанием.
Основной задачей позиционера является подача сжатого воздуха к приводу клапана, позволяющая штоку или валу клапана соответствовать заданному значению системы управления.Когда клапан требует дросселирования, часто используются позиционеры. Позиционер использует информацию о положении штока или вала клапана для открытия и закрытия клапана и подачи пневматического давления на привод.
Позиционер должен быть прикреплен к узлу регулирующего клапана или близко к нему. Позиционеры делятся на три типа в зависимости от типа управляющего сигнала, диагностических возможностей и протокола связи: пневматические аналоговые, цифровые и гибридные.
Регулирующие клапаны прямого действия и регулирующие клапаны обратного действия
Отказоустойчивый режим пневматического/пружинного клапана определяется действием как привода, так и корпуса клапана.
Привод прямого действия для клапанов с подвижным штоком давит на шток при повышении давления, тогда как привод обратного действия поднимает шток при повышении давления.
Корпуса клапанов прямого действия со скользящим штоком открываются при поднятии штока, в то время как корпуса клапанов обратного действия закрываются (закрываются) при подъеме штока.
Путем простого подбора подходящего типа привода и корпуса регулирующий клапан со скользящим штоком с пневматическим приводом может работать как при открытии, так и при закрытии воздухом.
Как показано на этом рисунке, наиболее типичные комбинации сочетают корпус клапана прямого действия с приводом клапана обратного или прямого действия:
Также могут использоваться корпуса клапанов обратного действия с противоположными результатами:
На левом рисунке показан корпус задвижки обратного действия, который открыт, жидкость обтекает шток, а широкий плунжер расположен значительно ниже области седла.