Расчет размера сварного шва — 2010
Данная программа выполняет расчет размера сварного шва и его ширины для всех узлов сетки на пересечении кромок удаленной детали, используя следующую процедуру.
- Задать локальную Систему координат сварного шва (СКС) для каждого узла.
- Определить толщину базового материала, tb, как толщину оболочки удаленной детали.
- Определить область сварки, Aw, на элемент длины:
- Односторонние (ОС) швы: Aw = tw, где tw — ширина шва
- Двухсторонние (ДС) швы: Aw = 2 × tw
- Определить момент сопротивления сечения сварки, Sw, на элемент длины:
- Угловые ДС-швы: Sw = tw x tb
- Стыковые ДС-швы: Sw = (4 / 3) × (tw3 / tb) – 2 × tw
- Угловые или стыковые ОС-швы: Sw = tw2 / 6
- Для каждого узла на пересечении кромок удаленного элемента рассчитать компоненты силы и момент на основе локальной системы СКС.
 Для ДС-швов необходимо разделить величину силы на 2 (расчеты проводятся на единицу длины сварки, а не сварного шва).
Для ДС-швов необходимо разделить величину силы на 2 (расчеты проводятся на единицу длины сварки, а не сварного шва).- Fs = Поперечная сила вдоль локальной оси Us.
- Fw = Поперечная сила вдоль локальной оси Uw .
Fj = Нормальная сила вдоль локальной оси Uj. Положительные значения Fj означают, что верхняя грань удаленной оболочки подвергается сжатию.
Mw = Узловой изгибающий момент, действующий вдоль локальной оси сварки Uw. Положительные значения Mw означают, что верхняя грань удаленной оболочки подвергается сжатию.
- Рассчитать узловую длину, Ln, для каждого узла как сумму ½ расстояния до каждого соседнего узла.
- Рассчитать компоненты нагрузки на единицу длины в зависимости от узловой длины для каждого узла:
- fs = (Fs / Ln) / Aw
- fw = (Fw / Ln) / Aw
- fj = (Fj / Ln) / Aw + ((Mw / Ln) / Sw)
- Рассчитать итоговую нагрузку на единицу длины для шва, fweld:
- fweld = sqrt ( fs2 + fw2 + fj2)
- Найти значение ширины шва, tw, для каждого узла на пересечении кромок удаленных деталей, при условии fсварка

- Рассчитать размер сварного шва, s, для каждого узла пересекающихся кромках удаленного элемента:
- Стыковые ОС- или ДС-швы: s = tw
- Угловые ОС- или ДС-швы 45°: s = sqrt(2) × tw
Расчет сварных швов — Справочник химика 21
Расчет сварных швов [c.89]
Расчет сварных швов на срез и изгиб [c.613]
Расчет сварных швов на срез [c.611]
Расчет сварных швов производится на изгиб и на срез. [c.167]
Элементарные проверочные расчеты сварных швов [c.371]
РАСЧЕТ СВАРНЫХ ШВОВ [c.98]
Расчет сварных швов. Сварные швы рассчитывают на изгиб и на срез. [c.87]
Расчет сварных швов укрепляющих колец [c.167]
Известно, что преимущественное накопление усталостных повреждений происходит в сварных швах, где за счет конструктивной формы (изменение сечения, геометрии сварного шва) и наличия технологических дефектов (непровары, подрезы, шлаковые включения и др. ) имеет место локальное повышение напряжений. При расчете сварных швов для перехода от значений внешних нагрузок я локальным напряжениям необходимо иметь значения коэ( к фициентов концентрации напряжений. Отсутствие систематизированных значений этих коэффициентов не позволяет провести полную оценку их величины. Наиболее полным представляется метод [c.43]
) имеет место локальное повышение напряжений. При расчете сварных швов для перехода от значений внешних нагрузок я локальным напряжениям необходимо иметь значения коэ( к фициентов концентрации напряжений. Отсутствие систематизированных значений этих коэффициентов не позволяет провести полную оценку их величины. Наиболее полным представляется метод [c.43]
При расчете на прочность сварных стыковых соединений за расчетное сечение принимается толщина свариваемого основного металла. Расчетная высота угловых швов принимается равной 0,7 величины катета шва. При автоматической сварке под слоем флюса, обеспечивающей глубокое проплавление основного металла, расчетная высота шва принимается равной его катету. При всех расчетах сварных швов на прочность усиление шва не учитывается.
При расчете сварных швов укрепляющего кольца внутренний кольцевой шов не рассчитывают, он создает запас прочности. [c.548]
Модель, подобная рассмотренной выше, исследовалась и раньше, например Ф. Блейхом [60] для расчета сварных швов, М. Го-ландом и Е. Рейсснером, а также Г. А. Перри для расчета клеевых соединений. [c.135]
Блейхом [60] для расчета сварных швов, М. Го-ландом и Е. Рейсснером, а также Г. А. Перри для расчета клеевых соединений. [c.135]
Расчет сварных швов на прочность. Общие данные. | ДЗЕН PROF-IL
Рис 1 — сварной шовРис 1 — сварной шов
Ставь лайк и подписывайся на свежие статьи!
Сайт источник: prof-il.ru
Таблица 1 — расчетное сопротивление сварных соединений (согласно СП 16.13330.2011 «Стальные конструкции», табл.4)Таблица 1 — расчетное сопротивление сварных соединений (согласно СП 16.13330.2011 «Стальные конструкции», табл.4)
Таблица 2 — определение временного сопротивления разрыва шва (согласно СП 16.13330.2011 «Стальные конструкции»)Таблица 2 — определение временного сопротивления разрыва шва (согласно СП 16.13330.2011 «Стальные конструкции»)
Согласно СП 16.13330.2011 «Стальные конструкции», таблица 4 получается: сварные швы «с угловыми швами», характеристика расчетного сопротивления шва — по металлу шва и по металлу границы сплавления; срез условный; Rwf = 0,55*Rwun / Ywm = 0,55*410 / 1,25 = 180,4МПа * Yc = 180,4 * 1,1 (Yс — коэффициент условия работы элементов и соединений стальных конструкций, табличные данные) =198,44 МПа — по металлу шва.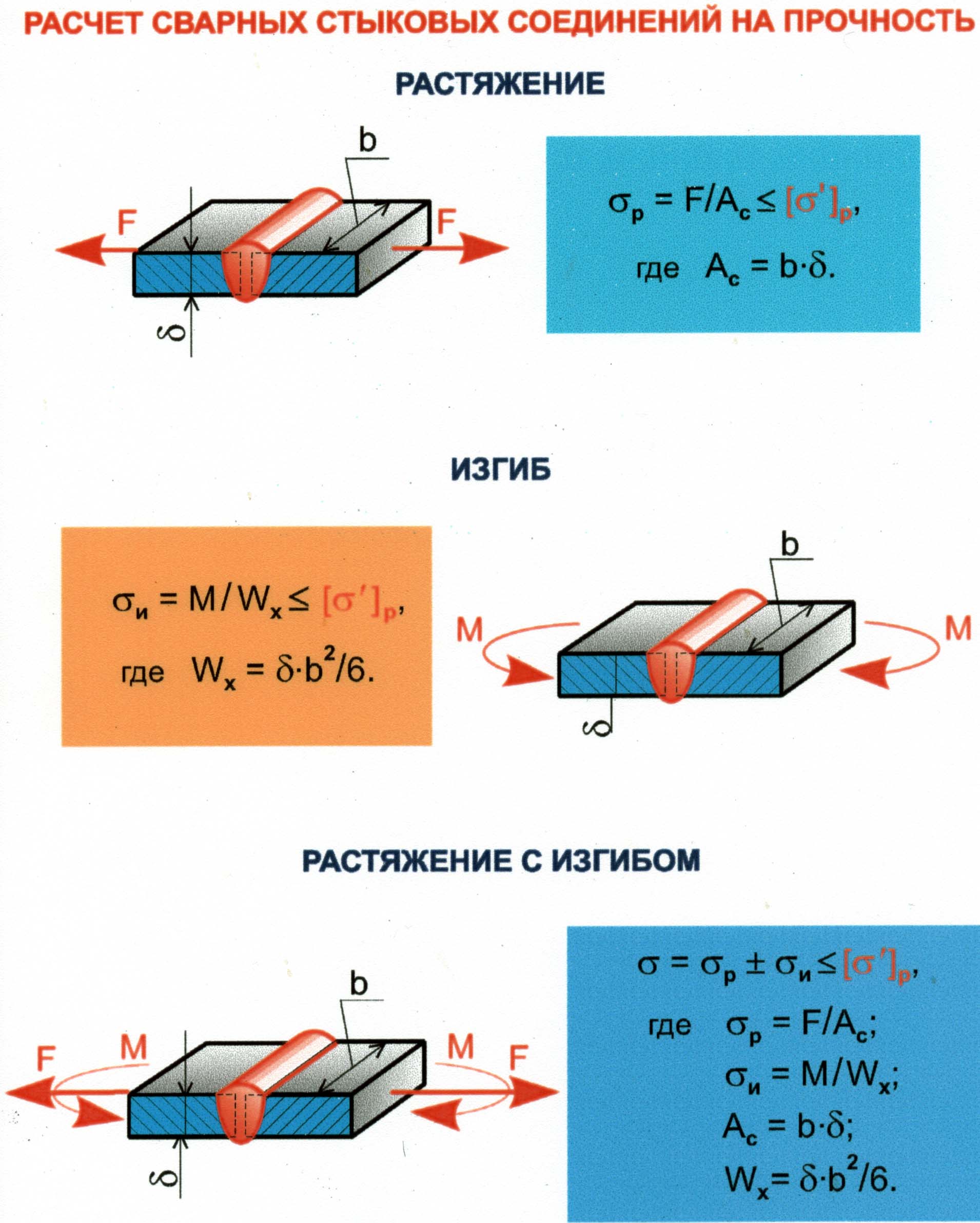
Rwz=0,45*Run = 0,45 * 360 = 162 МПа * 1,1 = 178,2 МПа — по границе сплавления металла.
Для расчета берем наименьшее значение — 178,2 МПа.
Значения коэффициентов надежности по металлу шва Ywm следует принимать:
Ywm = 1,25 — при Rwun ≤ 490 Н/мм2 (4900 кг/см2)
Ywm = 1,35 — при Rwun ≥ 590 Н/мм2 (5900 кг/см2)
Ссылка: указание по сварке
Таблица 3 — коэффициенты условий работы YсТаблица 3 — коэффициенты условий работы Yс
Берем пункт 6, элементы конструкций из стали с пределом текучести до 440МПа, несущие статическую нагрузку, при расчете на прочность по сечению, ослабленному отверстиями для болтов (кроме фрикционных соединений) — Yс=1,10
Таблица 4 — расчетное сопротивление для сталиТаблица 4 — расчетное сопротивление для стали
Разрушение углового сварного шва может произойти в двух плоскостях: по металлу шва, по границе сплавления, следовательно расчет угловых швов производится для этих двух сечений.
Много интересного в книге «Примеры расчета металлических конструкций» автор А.П.Мандриков.
Рис 2 — сечение угловых швов, А.П. МандриковРис 2 — сечение угловых швов, А.П. Мандриков
На рисунке показано сечение по границе сплавления, по металлу, катет шва Kf, безразмерный коэффициент Bz, Bf
Более подробно: расчет сварных швов
Статья дана для сведения.
Сайт источник: prof-il.ru
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}} {{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings. ТЕГИ}}
{{$элемент}}
{{l10n_strings.ПРОДУКТЫ}}
{{l10n_strings.DRAG_TEXT}}
ТЕГИ}}
{{$элемент}}
{{l10n_strings.ПРОДУКТЫ}}
{{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.ЯЗЫК}} {{$select.selected.display}} АВТОР}}
АВТОР}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}} Справочник— Расчеты Справочник
— Расчеты 2 0.5 дюймов 0,5 дюйма (А) ВЫСОТА (В) ОСНОВАНИЕ Объем сварного шва = .5B х А х 12 Вес стали = 0,283 фунта на куб. в. Вес сварного шва = (0,5 х 0,5) х 0,5 х 12 х 0,283 = 0,424 фунта. ВЕС НА ФУТ УГЛОВОГО СВАРНОГО ШВА В показанный ниже угловой шов, площадь поперечного сечения (треугольник) равна до половины основания, умноженного на высота, объем шва равен площади, умноженной на длину, а тогда вес сварного шва объем, умноженный на вес материала (стали) на кубический дюйм. Этот пример относится к угловому шву с
нет армирования. Аналогичные расчеты можно произвести для стыковых и нахлесточных соединений.
Эффективность осаждения
Эффективность осаждения электрода
или сварочная проволока указывает на часть этого продукта, которую вы можете
ожидается отложение в виде металла сварного шва.
Потери из-за шлака, брызг, дыма и в случае полуавтоматического
или процессы автоматической сварки,
концы обрезаются перед каждым сварным швом, а проволока, оставленная в питающем кабеле, не
процесс эффективен на 100%.Для оценки электрода
или расход проволоки, следующий средний
можно использовать значения эффективности осаждения.
Процесс осаждения
Эффективность под водой
Арка 99%
Газометаллическая дуга (98% А, 2% О
Этот пример относится к угловому шву с
нет армирования. Аналогичные расчеты можно произвести для стыковых и нахлесточных соединений.
Эффективность осаждения
Эффективность осаждения электрода
или сварочная проволока указывает на часть этого продукта, которую вы можете
ожидается отложение в виде металла сварного шва.
Потери из-за шлака, брызг, дыма и в случае полуавтоматического
или процессы автоматической сварки,
концы обрезаются перед каждым сварным швом, а проволока, оставленная в питающем кабеле, не
процесс эффективен на 100%.Для оценки электрода
или расход проволоки, следующий средний
можно использовать значения эффективности осаждения.
Процесс осаждения
Эффективность под водой
Арка 99%
Газометаллическая дуга (98% А, 2% О 
Помощь в расчете сварки — СВАРКА
Углеродные эквиваленты
Параметры сварки / предварительный нагрев
Эффективное тепловложение/время охлаждения
Твердость по ЗТВ
Индекс
Данные, рассчитанные этой программой, предназначены только для информации и не охватывают все детали процедуры сварки.Поэтому эта программа не дает гарантии в отношении свойств сварных соединений. В любом случае необходимо соблюдать основные стандарты сварки и строительства. Кроме того, следует принимать во внимание описание производственных свойств наших технических паспортов материалов и соблюдать все необходимые уровни тщательного контроля качества.
________________________________________________________________________________________________________
УГЛЕРОДНЫЕ ЭКВИВАЛЕНТЫ
Углеродные эквиваленты представляют собой упрощенные параметры, с помощью которых пытаются оценить влияние содержания легирующих элементов в стали путем суммирования содержания различных легирующих элементов с помощью определенной процедуры усреднения.
| CET | := | C + (Mn + Mo)/10 + (Cr + Cu)/20 + Ni/40 |
| СЕ | := | C + Mn/6 + (Cr + Mo + V)/5 + (Ni+ Cu)/15 |
| CEN | := | С + [ 0.75 + 0,25*tanh(20*(C — 0,12))] * [Si/24 + Mn/6 + Cu/15 + Ni/20 + (Cr + Mo + V + Nb)/5 + 5*B] |
| Р см | := | C + Si/30 + (Mn + Cu + Cr)/20 + Mo/15 + Ni/60 + V/10 + 5*B |
Укажите содержание легирующих элементов, указанное в сертификате проверки. Программа рассчитает различные углеродные эквиваленты.
Для CET-эквивалента, который является предпосылкой для следующего расчета параметров сварки, диапазон достоверности следующий (в весовых %):
| К: | 0. 05 — 0,32 05 — 0,32 |
| Си: | ≤ 0,80 |
| Мн: | 0,50 — 1,90 |
| Кр: | ≤ 1,50 |
| Ni: | ≤ 2,50 |
| Пн: | ≤ 0,75 |
| Медь: | ≤ 0,70 |
| В: | ≤ 0,18 |
| Номер: | ≤ 0,06 |
| Ти: | ≤ 0.12 |
| Б: | ≤ 0,005 |
Если содержание легирующих элементов выходит за пределы этого диапазона достоверности, этот элемент, а также параметр CET отмечаются красным цветом.
______________________________________________________________________________________________________________
ПАРАМЕТРЫ СВАРКИ / ПРЕДВАРИТЕЛЬНЫЙ НАГРЕВ
Расчет параметров сварки основан на методе B в EN 1011-2 (Сварка. Рекомендации по сварке металлических материалов. Часть 2. Дуговая сварка ферритных сталей), описанном в приложениях C и D к настоящему стандарту.
Этот метод описывает, как следует выбирать параметры сварки, чтобы избежать особенно холодного растрескивания в зоне термического влияния (ЗТВ). В любом случае для конкретной стали следует учитывать рекомендации по свойствам изготовления, приведенные в наших технических паспортах материалов. Кроме того, пользователь должен обеспечить соблюдение соответствующих стандартов, таких как EN 10 11.
Предварительный нагрев:
Предварительный нагрев очень полезен для предотвращения явления холодного растрескивания, поскольку он замедляет охлаждение ЗТВ и позволяет выйти водороду, образовавшемуся во время сварки.Кроме того, предварительный нагрев снижает ограничения, связанные со сваркой. Многослойные сварные швы можно начинать без предварительного нагрева, если выбрана подходящая последовательность сварки и достаточна межпроходная температура.
Температура предварительного нагрева – это самая низкая температура перед первым проходом сварки, ниже которой нельзя падать во избежание холодного растрескивания. Для многослойных сварных швов этот термин относится к температуре второго и последующих проходов сварки и также называется межпроходной температурой.В целом две температуры идентичны.
Для многослойных сварных швов этот термин относится к температуре второго и последующих проходов сварки и также называется межпроходной температурой.В целом две температуры идентичны.
Температура предварительного нагрева зависит от следующих входных данных:
- Углеродный эквивалент CET (см. выше): CET можно указать здесь или рассчитать по содержанию легирующих элементов в меню «Углеродный эквивалент». CET вставляется в % вес.
- Толщина листа d: Толщина листа вводится в мм. Следует учитывать, что влияние толщины листа имеет второстепенное значение при толщине листа более 60 мм из-за трехмерного теплового потока.
- Содержание водорода HD: Содержание водорода h3 указано в мл/100 г. Здесь можно либо ввести значение от 1 до 20 мл/100 г, либо выбрать типичное значение в зависимости от используемого процесса сварки:
Типичное содержание водорода в сварочных материалах
| Метод | Обычное содержание водорода [мл/100 г] |
|---|---|
| Ручная металлическая дуга MMA | 5 |
| Дуговая сварка MIG/MAG в газовой среде | 3 |
| Дуговая сварка с флюсовой сердцевиной Basic FCAW | 5 |
| Базовая дуговая сварка под флюсом | 5 |
- Эффективное тепловложение: Эффективное тепловложение Q, которое определяется произведением тепловложения E на коэффициент полезного действия h , Q = h *E, здесь выражается в кДж/мм.
 Существует два способа учета влияния эффективного подводимого тепла.
Существует два способа учета влияния эффективного подводимого тепла.
— Зависимость между температурой предварительного нагрева и энергией сварки отображается в окне параметров сварки, которое отображается после заполнения всех необходимых данных.
— Кроме того, температуру предварительного нагрева можно рассчитать в явном виде, введя либо эффективную подводимую теплоту Q в кДж/мм, либо подводимую теплоту E в кДж/мм и коэффициент эффективности h, который зависит от используемого процесса сварки. Фактор эффективности подробно описан в _следующем разделе_.
Исходя из приведенных выше данных, минимальная температура предварительного нагрева рассчитывается следующим образом:
| Тп = | 697*CET+ 160*tanh(d/35)+62*HD 0,35 + (53*CET-32)*Q-328 |
Диапазон допустимости этой формулы:
| CET: | 0,2 % — 0,5 % |
| д: | 10 мм — 90 мм |
| HD: | 1 мл/100 г — 20 мл/100 г |
| Вопрос: | 0. |
Влияние времени охлаждения:
Цикл температура-время имеет большое значение для механических свойств сварного соединения после сварки. В частности, на него влияют геометрия сварки, подводимое тепло, температура предварительного нагрева, а также детали наплавленного слоя. Обычно температурно-временной цикл во время сварки выражается временем t 8/5 , которое представляет собой время, за которое происходит охлаждение наплавленного слоя с 800°С до 500°С.
Максимальная твердость в ЗТВ обычно уменьшается с увеличением времени охлаждения t8/5. Если заданное максимальное значение твердости не должно превышаться для конкретной стали, параметры сварки должны выбираться таким образом, чтобы время охлаждения t 8/5 не опускалось ниже определенного значения.
С другой стороны, увеличение времени охлаждения приводит к уменьшению ударной вязкости ЗТВ, что означает снижение показателей ударной вязкости, измеренных в V-испытании по Шарпи, или увеличение температуры перехода при ударной нагрузке по Шарпи-V энергия. Поэтому параметры сварки должны быть выбраны таким образом, чтобы время охлаждения не превышало определенного значения.
Поэтому параметры сварки должны быть выбраны таким образом, чтобы время охлаждения не превышало определенного значения.
В целом, для свариваемых мелкозернистых марок конструкционной стали время охлаждения для заполнения и покрытия слоев сварного шва должно составлять от 10 до 25 с в зависимости от указанной здесь марки стали. После соответствующей проверки нет проблем с применением и других значений времени охлаждения t 8/5 при условии, что требования к качеству свариваемой конструкции полностью выполнены и проведена соответствующая аттестация технологии сварки.
Кроме того, вы можете рассчитать диаграмму параметров сварки, которая показывает возможную тепловложение — температуры предварительного нагрева для заданного максимального и минимального времени охлаждения. Если вы хотите рассчитать явное время охлаждения, используйте следующий раздел (_Время охлаждения_).
Следующие параметры влияют на время охлаждения, либо на его расчет, либо на его выбор, и могут быть вставлены сюда для получения оптимизированных параметров сварки:
- Толщина листа d: Толщина листа вводится в мм.
 Следует учитывать, что влияние толщины листа имеет второстепенное значение при толщине листа более 60 мм из-за трехмерного теплового потока. Геометрия сварки: Влияние геометрии сварки учитывается коэффициентами геометрии сварки F 2 и F 3 для двух- и трехмерного теплового потока. Значения коэффициента геометрии шва для типовых геометрий шва:
Следует учитывать, что влияние толщины листа имеет второстепенное значение при толщине листа более 60 мм из-за трехмерного теплового потока. Геометрия сварки: Влияние геометрии сварки учитывается коэффициентами геометрии сварки F 2 и F 3 для двух- и трехмерного теплового потока. Значения коэффициента геометрии шва для типовых геометрий шва:
| Геометрия сварного шва | F 2 (двумерный) | F 3 (трехмерный) |
| Наплавка | 1.0 | 1,0 |
| Заполнение проходов стыковых швов | 0,9 | 0,9 |
| Покрытие проходов стыковых швов | 1,0 | 0,9 — 1,0 |
| Однопроходный угловой шов (угловое соединение) | 0,9 — 0,67* | 0,69 |
| Однопроходный угловой шов (тройник) | 0,45 — 0,67* | 0,67 |
Фактор геометрии сварки F 2 зависит от отношения эффективного подводимого тепла к толщине листа. Приближаясь к трехмерному, тепловой поток F 2 уменьшается для случая однопроходного углового шва на угловом соединении и увеличивается для однопроходного углового шва на тавровом соединении. Поэтому здесь может потребоваться адаптивный расчет.
Приближаясь к трехмерному, тепловой поток F 2 уменьшается для случая однопроходного углового шва на угловом соединении и увеличивается для однопроходного углового шва на тавровом соединении. Поэтому здесь может потребоваться адаптивный расчет.
Здесь можно выбрать приведенные выше коэффициенты. Кроме того, возможен свободный ввод данных в диапазоне от 0 до 1.
- Эффективное тепловложение: Эффективное тепловложение Q, которое определяется как произведение тепловложения E на коэффициент полезного действия h , Q = h *E, здесь выражается в кДж/мм.Влияние эффективного подвода тепла в зависимости от температуры предварительного нагрева/межпрохода и минимального и максимального времени охлаждения t 8/5 показано на диаграмме параметров сварки, которая строится после достижения необходимых значений.
- Предварительный нагрев/Температура между проходами: Влияние времени предварительного нагрева также показано на диаграмме параметров сварки.

- Максимальное и минимальное время охлаждения:
Из приведенных выше данных можно рассчитать время охлаждения t 8/5 , если принять трехмерный тепловой поток:t 8/5 = (6700-5*T P )*Q* (1/(500-TP)-1/(800-T P ))*F 3
При двумерном тепловом потоке время охлаждения зависит от толщины пластины и используется следующая формула:
t 8/5 = (4300-4.3*T P )*10 5 *Q 2 /d 2 * (1/(500-T P ) 2 -1/(800-T 6 2 9017) 2 900 )*F 2
Физически допустимо только большее значение, полученное из двух приведенных выше формул. Часто рассчитывают толщину переходной пластины dt, при которой происходит переход между двумерным и трехмерным тепловым потоком. Толщина этой переходной пластины:
d t = SQR(((4300-4.3*T p )*10 5 /(6700-5*T p )*Q*(1/(500 -T P ) 2 -1/(800-T P ) 2 )/ (1/(500-T P ) -1/(800-T P )))
Максимальное и минимальное время охлаждения зависит от марки свариваемой стали.
 Здесь можно выбрать время охлаждения, рекомендованное продуктами марки Dillinger. Как описано выше, другое время охлаждения может быть выбрано при условии, что требования к качеству свариваемой конструкции полностью выполнены и проведена соответствующая квалификация процедуры сварки. Поэтому также возможен свободный ввод времени охлаждения. В любом случае необходимо также учитывать рекомендации, приведенные в наших технических паспортах материалов.
Здесь можно выбрать время охлаждения, рекомендованное продуктами марки Dillinger. Как описано выше, другое время охлаждения может быть выбрано при условии, что требования к качеству свариваемой конструкции полностью выполнены и проведена соответствующая квалификация процедуры сварки. Поэтому также возможен свободный ввод времени охлаждения. В любом случае необходимо также учитывать рекомендации, приведенные в наших технических паспортах материалов.
Блок параметров сварки
Из приведенных выше параметров создается поле параметров сварки, в котором указаны возможные комбинации эффективного подводимого тепла Q и температуры предварительного нагрева/между прохода T p , удовлетворяющие следующим условиям:
- достаточный предварительный нагрев,
- Время охлаждения меньше максимального значения, определенного выше,
- Время охлаждения превышает минимальное значение, определенное выше.
Кроме того, возможен прямой расчет температуры предварительного нагрева путем указания либо эффективной подводимой теплоты Q, либо подводимой теплоты E и коэффициента полезного действия h.
______________________________________________________________________________________________________________
ЭФФЕКТИВНАЯ ТЕПЛОПОДАЧА/ ВРЕМЯ ОХЛАЖДЕНИЯ
Одним из определяющих параметров при расчете параметров сварки является эффективное тепловложение. По входным данным
- Электрическое напряжение U [В]
- Электрический ток I [А]
- Скорость сварки v [мм/мин]
сначала вычисляется подводимая теплота E [кДж/мм] по формуле
E = U*I/v * (60/1000) в кДж/мм.
Результат эффективного подводимого тепла Q представляет собой подводимое тепло путем умножения на коэффициент энергоэффективности h, который зависит от применяемого процесса сварки.
Q = ч * Е
с КПД
Коэффициент энергоэффективности для различных сварочных процессов
| Процесс сварки | Коэффициент полезного действия ч |
| Ручная металлическая дуга | 0. 8 8 |
| Погружная дуга | 1,0 |
| Металлический активный газ (MAG) | 0,8 |
| Металлический инертный газ (MIG) | 0,7 |
| Порошковая порошковая проволока (FCAW) | 0,9 |
| Вольфрамовый инертный газ (TIG) | 0,7 |
Время охлаждения
Время охлаждения между 800°C и 500°C t 8/5 является наиболее важным параметром для определения параметров сварки, применяемых при сварке мелкозернистых конструкционных сталей.Основные причины подробно описаны выше.
В этом меню вы можете легко рассчитать это время охлаждения, указав следующие значения:
- Эффективная тепловая мощность Q [в кДж/мм]
- Температура предварительного нагрева T p [°C]
- Толщина листа d [мм]
- Коэффициенты геометрии сварки F 2 /F 3 : Для коэффициентов геометрии сварки необходимо выбрать подходящую геометрию сварки из таблицы, кроме того, также свободный ввод в диапазоне от 0 до 1.
 0 можно.
0 можно.
Из приведенных выше данных можно рассчитать время охлаждения t8/5, если принять трехмерный тепловой поток:
t 8/5 = (6700-5*T P )*Q* (1/(500-T P )-1/(800-T P ))*F 3
Если тепловой поток двухмерный, время охлаждения зависит от толщины пластины и используется следующая формула:
t 8/5 = (4300-4,3*T P )*10 5 *Q 2 /d 2 * (1/(500-T 7 -1904 2
) ) /(800-T P ) 2 )*F 2Физически допустимы только большие значения, полученные из двух приведенных выше формул.Часто рассчитывают толщину переходной пластины dt, при которой происходит переход между двумерным и трехмерным тепловым потоком. Толщина этой переходной пластины определяется следующим образом:
d t = SQR(((4300-4.3*T p )*10 5 /(6700-5*T p )*Q*(1/(500-T P
) При этом указывается, имеет ли место двумерный или трехмерный тепловой поток.
Следует учитывать, что допущения, лежащие в основе формул для времени охлаждения, часто выполняются не полностью. Поэтому рассчитанные значения могут отклоняться от реальных значений до 10 %.
______________________________________________________________________________________________________________
ПИКОВАЯ ТВЕРДОСТЬ В ЗОНЕ ТЕРМИЧЕСКОГО ВОЗДЕЙСТВИЯ
Пиковая твердость в зоне термического влияния (ЗТВ) часто считается признаком качества изготовления сварного соединения и поэтому часто измеряется во время утверждений технологии сварки и испытаний сварки.Верхние пределы твердости HAZ определены в стандартах на сварку, таких как DIN EN ISO 15614-1.
Физически максимальная твердость зависит от скорости охлаждения в крупнозернистой зоне ЗТВ. Чем выше скорость охлаждения, тем выше результирующая твердость ЗТВ. Более низкая скорость охлаждения приводит к более гладкой зернистой структуре, такой как бейнит и феррит. Поэтому также время охлаждения t 8/5 часто используется для оценки максимальной твердости в зоне HAZ.
Вторым важным влияющим фактором является химический состав стали, поскольку он определяет количество различных зернистых структур, образующихся при охлаждении.Обычно легирующие элементы, такие как углерод, молибден, марганец и хром, повышают прокаливаемость и смещают падение твердости к более длительному времени охлаждения. Но также на твердость различных зернистых структур влияет легирующий состав.
Расчет значений твердости
Программа предлагает две процедуры для оценки пиковой твердости в ЗТВ, формулу Дюрена и формулу Юриока. Обе формулы были разработаны путем систематических исследований вместе с регрессионным анализом твердости ЗТВ в зависимости от химического состава и времени охлаждения.
Здесь можно ввести химический состав, а затем рассчитать теоретическую твердость по формуле Дюрена или Юриока в зависимости от времени охлаждения.
Кроме того, значение пиковой твердости для специального времени охлаждения можно рассчитать, введя время охлаждения.
Твердость по Дюрену рассчитывается по следующим формулам:
Мартенситная твердость HV M
HV M = 802 x C + 305
Твердость по бейниту HV B
HV B = 350 x CE* + 101
CE* = C +Si/11 +Mn/8 +Cu/9 +Cr/5 +Ni/17 +Mo/6 +V/3
Результирующая твердость:
HV = 2019x[ C(1- 0,5 * log t 8/5 ) + 0,3(CE*-C)] + 66x[1 — 0,8 x log t 8/5 ]
Если HV < HV M и HV > HV B , то твердость по Юриока рассчитывается по формуле
HV = 0,5 (HV M + HV B ) — 0,455 (HV M — HV B ) арктангенс t*
| с | ВН м | := | 884 х С (1 — 0,3 С²) + 294 |
| ВН б | := | 145 + 130 x тангенс (2,65 CE 2 — 0,69) | |
| СЕ 1 | := | C + Si/24 + Mn/6 + Cu/15 + Ni/12 + Cr/8 + Mo/4 + ΔH | |
СЕ 2 | := | C+Si/24+Mn/5+Cu/10+Ni/18+Cr/5+Mo/2,5+Nb/3+V/5 | |
| СЕ 3 | := | C + Mn/3,6 + Cu/20 + Cr/5 + Ni/9 + Mo/4 | |
| т* | := | 4 (ln t 8/5 — ln t nb )/(ln t нм — ln t nb ) -2 | |
т номер | := | exp (10,6 x CE 1 — 4,8) | |
т морских миль | := | exp (6,2 x CE 3 + 0,74) |
Обратите внимание, что ΔH — это термин, введенный для учета сильного упрочняющего действия бора, например;
| ΔH | = | 0 | , когда B ≤ 1 ppm, |
| ΔH | = | 1. 5 (0,02-Н) 5 (0,02-Н) | , если B ≤ 2 частей на миллион, |
| ΔH | = | 3,0 (0,02-Н) | , когда B ≤ 3 частей на миллион, и |
| ΔH | = | 4,5 (0,02-Н) | , когда B ≤ 4 частей на миллион, |
Кроме того, максимальные значения твердости, допустимые по DIN EN ISO 15614-1, можно вызвать с помощью кнопки «Макс. твердость», а максимальное значение твердости можно выбрать и вставить в диаграммы твердости
Максимально допустимые значения твердости, HV 10 согласно DIN EN ISO 15614-1.
| Группа стали CR ISO 15608 | без термической обработки | с термообработкой |
| 1 и , 2 | 380 | 320 |
| 3 б | 450 | 380 |
| 4, 5 | 380 | 320 |
| 6 | — | 350 |
9. 1 1 9,2 9,3 | 350 450 450 | 300 |
a Если требуются испытания на твердость
b Для сталей с R eH мин. > 890 МПа требуются специальные соглашения.
1) Стальные с виду. ReH ≤ 460 МПа
2) Термомеханически катаные стали с мин. ReH > 360 МПа
3) Закаленные и отпущенные стали с мин. ReH > 360 МПа
Термическая обработка после сварки (PWHT)
Для сварного соединения, обработанного послесварочной термической обработкой, также можно рассчитать снижение твердости из-за этой термической обработки по формуле Окумура:
| ДХВ = | [884C+177-197CE 2 +16,5(HP-21,5)]xMM-7CE 2 +26 |
| +[ 18 ( HP-18 )2 — 138 ] V 1/2 | |
| +[ 20 ( HP-18) 2 — 268 ] Nb 1/2 | |
| +[ 25 (HP-17,3) 2 — 55 ] Мо 1/2 | |
| с ММ = | доля мартенсита = 0,5 — 0,455 арктангенса t* |
| CE 2 и т* | из формулы Юриока |
Здесь HP представляет собой так называемый параметр Холломона HP = (T+273)/1000 x (20 + log t) с температурой термообработки в °C и временем отжига t в час. Для расчета необходимо ввести этот параметр или можно ввести время и температуру отжига.
Для расчета необходимо ввести этот параметр или можно ввести время и температуру отжига.
После ввода входных данных на диаграмме показана зависимость снижения твердости, вызванного PWHT, от времени охлаждения, а также разностная функция между снижением твердости по Юриоке и по Окумуре. Специальное значение можно оценить, введя время охлаждения.
Углеродные эквиваленты
CET-эквиваленты
Время охлаждения
Дюрена-твердость
ФАКТОР ЭФФЕКТИВНОЙ ФАКТОР
Твердость в HAS
Тепловая зона
Эффективный тепловой вход
HOLLOMON-PARAMETER
ГОРОДА
Тепловой вход
Окумура-твердость
Предварительный нагрев
Температура предварительного нагрева
Переход
толщина
Геометрия сварного шва
Юриока-Твердость
(PDF) Расчет методом конечных элементов и оценка статических напряжений в несущих угловых сварных швах
12/13
Расчет сварного шва в примере.Метод конечных элементов дает более реалистичное распределение напряжений
и, следовательно, более экономичную конструкцию. С другой стороны, нелинейный анализ показывает
С другой стороны, нелинейный анализ показывает
полное перераспределение напряжений. Особенно это происходит в сварном соединении с неравномерным распределением линейных напряжений. Насколько может быть использован связанный с этим пластиковый запас, можно проверить только
испытаниями. В связи с этим следует иметь в виду, что анализ напряжений может содержать неопределенности, т.е.г. измененное распределение нагрузки из-за несущей конструкции. Кроме того, дефекты сварки
могут повлиять на прочность.
7 Выводы
Из расчетов напряжений на примере угловой сварной подъемной петли
сделаны следующие выводы:
1. Составляющие номинального напряжения и
τII
в угловом шве, которые относятся к статической прочности
в соотв.по нескольким кодам (например, Еврокод, DIN 18800), обычно рассчитываются по относительно простым уравнениям (сила на площадь сечения или момент на модуль сечения). В дополнение
к диагональному сечению через сварной шов также могут быть рассмотрены сечения, параллельные соседним пластинам
в случае угловых швов под углом 90°, если сварные швы идеализированы как линейное соединение и напряжения
относятся к толщине горловины
a
. Компоненты напряжения могут быть легко переведены в напряжения в диагональном сечении.
Компоненты напряжения могут быть легко переведены в напряжения в диагональном сечении.
2. Допущения должны быть сделаны, в частности, для распределения напряжения из-за крутящего момента,
, который может создавать напряжения, действующие поперек или параллельно сварному шву. Как показано на примере, большие дополнительные напряжения
могут быть связаны с ограничением коробления.
3. Простые конечно-элементные модели с пластинчатыми или оболочечными элементами, которые непосредственно соединяются в сварном соединении
, дают продольные силы и моменты, которые могут быть преобразованы в компоненты номинального напряжения в сварном шве.
4. Грубые трехмерные сетки конечных элементов, где угловой шов представлен только одним или двумя сплошными элементами
в поперечном сечении, дают результаты, которые могут занижать напряжения в сварном шве
более чем на 50 %, если они возникают из-за напряжений только в сварных элементах или
противоположных элементах пластин. Это связано с тем, что узловые силы между элементами
Это связано с тем, что узловые силы между элементами
создают также напряжения в соседних элементах в корневом зазоре, которые необходимо учитывать
при расчете средних напряжений сварки.Даже в этом случае различия могут быть относительно большими, как показал пример. Надежными являются только напряжения, полученные от узловых сил
, действующих в сечении сварного шва и отнесенных, как обычно, к толщине шва.
5. Модели с мелкими ячейками показывают высокие пики напряжения, в основном вблизи носка сварного шва и, возможно, корня шва.
Для оценки статической прочности компоненты номинального напряжения в сварном шве снова могут быть получены путем усреднения напряжений элемента.
Рекомендуется использовать диагональный разрез, чтобы избежать срезов из-за высоких напряжений на кромке сварного шва. Однако напряжения в соседних элементах на
корневом зазоре должны быть учтены и в мелкоячеистых моделях. Пренебрежение ими привело к примеру
, где три элемента располагались по толщине горловины, к занижению
более чем на 20 %.
6. Перед достижением предельного состояния текучесть сварного шва и прилегающего основного материала заново распределяет напряжения, как показано на примере.Пики напряжений, обнаруженные при линейном анализе мелкой трехмерной сетки конечных элементов, больше не существуют. Это оправдывает относительно простой
анализ усредненных напряжений в сварном шве.
7. Эквивалентные напряжения, рассчитанные в соответствии с нормами, показывают большие различия между анализами. В частности, аналитические формулы дают высокие напряжения на концах сварного шва
при плоскостных изгибающих и скручивающих нагрузках, что приводит к консервативному расчету.
Здесь анализ методом конечных элементов дает более реалистичные значения, так как напряжения усредняются по
сварному шву. Дальнейшее перераспределение напряжений вдоль сварных швов из-за текучести
может значительно увеличить несущую способность, однако ее использование при проектировании под вопросом
Общая процедура, описанная в расчете конструкции сварного шва для гибочного изделия, будет применима и в этой статье, с единственным существенным отличием в использовании полярного момента инерции (J) вместо момента инерции площади (I), поскольку мы говорим про торсион здесь.
Немного сбивает с толку? Ну, мы собираемся понять процедуру подробно шаг за шагом здесь на следующем примере:
Постановка задачи: Посмотрите на приведенную ниже конструкцию сварного соединения, это конструкционное соединение консольного типа, в котором угловые сварные швы подвергаются крутящему моменту, возникающему из-за нагрузки F. Рассчитайте размер углового сварного шва, необходимый для применения .
Расчет прочности углового сварного шва при кручении Пример
Дано,
F= 20000 Н
Х = 200 мм
Y = 150 мм
Z=100 мм
Решение:
Шаг 1: Расчет центра тяжести: Определите центр тяжести (ЦТ) всей схемы углового сварного шва.В приведенном выше примере у нас есть область сварки прямоугольной формы. Итак, очевидно, ЦТ будет находиться на пересечении двух диагоналей прямоугольника. И мы можем найти COG, который помечен как C, как показано ниже:
И мы можем найти COG, который помечен как C, как показано ниже:
a=Z/2=50 мм
b = Y/2 = 75 мм
Шаг 2: Рассчитайте площадь единичного сварного шва (Au) : Площадь единичного сварного шва для примера задачи:
Au= 2*(Y+Z) = 2*(150+100) = 500 кв.мм
Шаг 3: Рассчитайте полярный момент инерции единичного горловины (Ju): Полярный момент инерции любой формы представляет собой сумму моментов инерции площади относительно оси XX и оси YY. Форма сварного соединения в приведенном выше примере имеет прямоугольную форму с двумя сторонами Y и Z соответственно.
Уравнение для расчета полярного момента инерции (единица длины горловины) для углового сварного соединения прямоугольной формы:
Ju=(Y+Z) 3 /6=(150+100) 3 /6 = 2604166.66 мм 3
Шаг 4: Расчет расчетной прочности (Pw): Расчетная прочность сварного шва для материала может быть рассчитана с использованием уравнения 2 как:
Pw=0,5*fu= 0,5*430 Н/мм 2 = 215 МПа
(При условии предела прочности при растяжении основного материала 430 Н/мм 2 )
Шаг 5: Рассчитать макс. Напряжение прямого сдвига в вертикальном направлении ( τsv) : Максимальное напряжение прямого сдвига, возникающее в сварном соединении, определяется как:
Напряжение прямого сдвига в вертикальном направлении ( τsv) : Максимальное напряжение прямого сдвига, возникающее в сварном соединении, определяется как:
τs=F/Au=20000/500 = 40 Н/мм 2
Шаг 6: Расчет макс. Напряжение сдвига при кручении в горизонтальном направлении в любом углу ( τth) : Причина, по которой выбрана угловая точка сварного шва: напряжение сдвига при кручении будет максимальным в углу, поскольку расстояние между точкой угла и центром тяжести сечение максимальное.
Напряжение сдвига при кручении, как правило, можно найти из уравнения:
τt = (T*r) / Ju……………………………….экв.a
где,
T = приложенный крутящий момент = F*[X+(Y-b)]=20000*[200+(150-75)]=5500000 Н-мм
(см. рисунок выше)
r = расстояние между точкой интереса на сварном шве и центром тяжести секции
Теперь, в случае горизонтального напряжения сдвига при кручении в любом углу,
r = a = 50 мм
Итак, из экв. а :
а :
τth= (T*r) / Ju = 5500000*50 / 2604166,66 = 105,6 Н/мм 2
Шаг 7: Расчет макс. Напряжение сдвига при кручении в вертикальном направлении в любом углу (τtv): Вышеупомянутое экв. будет использоваться здесь снова:
В случае вертикального напряжения сдвига при кручении в любом углу:
r = b = 75 мм
Итак, из экв.а:
τtv= (T*r) / Ju = 5500000*75 / 2604166,66 = 158,4 Н/мм 2
Шаг 8: Расчет результирующего напряжения сдвига в углу (τ):
Результирующее напряжение сдвига ( τ) = √ [(общее горизонтальное касательное напряжение) 2 + (общее вертикальное касательное напряжение) 2 ]……………………………. eq .б
eq .б
Для приведенного выше примера
Суммарное горизонтальное касательное напряжение = τth= 105.6 Н/мм 2
Полное напряжение вертикального сдвига = τsv + τtv = 40 + 105,6 = 145,6 Н/мм2
Итак, из экв.б ,
Результирующее напряжение сдвига (τ) = √ [105,6 2 + 145,6 2 ] = 179,86 Н/мм2
Шаг 9: Рассчитайте размер сварочного шва (t): Используйте экв.6 из предыдущей статьи здесь:
t= τ/Pw = 179,86 / 215 = 0,83 мм
Шаг 10: Рассчитайте размер сварного участка (L): Используйте eq.7 из предыдущей статьи, как показано ниже,
L=1,414*t = 1,414*0,83 = 1,173 мм
Наконец, мы получили требуемый размер сварного шва (длина стороны) как 3 мм (рядом с 1,173 мм, как рассчитано) в результате примера расчета конструкции углового сварного шва. Расчет выполнен на основе метода напряжения сварного шва, описанного в BS 5950.
Расчет выполнен на основе метода напряжения сварного шва, описанного в BS 5950.
Экспресс-расчет остаточных напряжений в разнородных стыковых сварных швах S355–AA6082
4.2. Аналитическая модель
Для записи уравнений, управляющих задачей, в матричной форме (основные уравнения, уравнения равновесия и совместности) сварные пластины были разделены на дискретное число ( n ) стержней. Ради простоты все стержни имели одинаковую ширину ( b ), а n были выбраны достаточно большими, чтобы учесть температурный градиент вблизи линии сварки с хорошим приближением.Предполагалось, что на каждом временном шаге температура каждого бруска одинакова и зависит только от его координаты х (т. е. Т = Т(х, t )). Другими словами, температурный градиент в направлении y не учитывался, и эта гипотеза становится все более и более верной по мере увеличения скорости сварки. Что касается КЭ модели, то граничные условия применялись на концах пластины согласно процессу HYB ( U x = 0 для x = 0 и для x = 2B , где U x смещение в направлении x , а B – ширина пластины, а граничные условия в направлении y описываются уравнением совместимости (11)). Использовался критерий текучести фон Мизеса, вязкопластическими эффектами материалов пренебрегали; предел текучести, модуль упругости и коэффициент теплового расширения обоих материалов считались функциями температуры, как описано уравнениями (A1)–(A14).
Использовался критерий текучести фон Мизеса, вязкопластическими эффектами материалов пренебрегали; предел текучести, модуль упругости и коэффициент теплового расширения обоих материалов считались функциями температуры, как описано уравнениями (A1)–(A14).
Схематическое изображение сварных пластин с боковыми ограничениями и линией сварки, выделенной красным цветом.
Если Ny,i и Nx,i — силы на поперечных сечениях в стержне i -й, возникающие от внутренних напряжений и нормальные к осям x и y соответственно, уравнения равновесия сил и импульса можно записать в матричной форме () следующим образом [21]:
где
C¯=[1d1……1di……1dn]
(7)
N¯y=[Ny1…Nyi…Nyn]
(8)
где n — количество дискретных баров, а di — x -расстояние бара i -го от начала координат ().
При гипотезе об упругом идеально пластическом поведении материалов определяющие уравнения имеют вид: +qpix+Δqpix для i=1…n
(10)
где q¯y — вектор, содержащий полные удлинения каждого дискретного стержня в продольном направлении; qeiy – упругий вклад в удлинение i -го стержня, определяемый законом Гука; qtiy — удлинение i -го стержня из-за теплового расширения; qpiy – пластическая деформация, накопленная на предыдущих временных шагах для и -го стержня; Δqpiy – пластическая деформация и -го стержня на текущем временном шаге; qix – полное удлинение стержня i в направлении x , qeix – упругий вклад в удлинение стержня x в направлении i , и он подчиняется закону Гука; qtix — удлинение в x i -го стержня вследствие теплового расширения; qpix – пластическая деформация в направлении x для i -го стержня, накопленная на предыдущих временных шагах; Δqpix – пластическая деформация i -го стержня в направлении x , рассчитанная на текущем временном шаге.
Наконец, уравнения совместимости:
где u¯ — вектор смещения, связанный со степенями свободы δ и θ, как показано на рис.
Схематическое изображение деформированной и недеформированной конфигурации сварных пластин.
Используя критерий фон Мизеса, материал текучести, когда:
где σуилд — предел текучести сплава (т. е. С355 или АА6082) при соответствующей температуре.
Уравнение (9) можно записать следующим образом: 14)
где A¯ — диагональная матрица, члены которой равны (L/(E(Ti)db)) (где Ti — температура i -го бара на рассматриваемом временном шаге), Ax¯ — вектор, в котором каждый элемент представлен слагаемым (νNx/(E(Ti)d ) ), At¯ — другая диагональная матрица, члены которой равны Lα(Ti), а T¯ — вектор, содержащий температуры для каждого стержня.
Используя уравнения (11) и (14), вектор Ny¯ может быть выражен уравнением:
N¯y=A¯−1(C¯u¯+A¯x−A¯t(T¯− T¯0)−q¯py−Δq¯py)
(15)
И из комбинации (15) и (5):
u¯=[C¯TA¯−1C¯]−1C¯ TA¯−1(−A¯x+A¯t(T¯−T¯0)+q¯py+Δq¯py)
(16)
Наконец, из уравнений (10) и (12) можно получить следующее уравнение:
Nx=1bdL∑1E(Ti)(vb∑NiyE(Ti)−b∑α(Ti)(Ti−T0)−∑(qpix+∆qpix))
(17)
Неизвестными терминами были Δqpiy и Δqpix. Процедура расчета началась с предположения, что увеличение пластической деформации (Δqpiy), а также сила в поперечном ( x ) направлении изначально равны нулю. Используя уравнение (3), был рассчитан вектор температуры (температура каждого стержня) и, следовательно, свойства материала (зависящие от температуры) и матрицы A¯, Ax¯ и At¯. При таких условиях было определено первое значение Ny¯ с использованием уравнений (15) и (16). Затем было наложено следующее условие:
Процедура расчета началась с предположения, что увеличение пластической деформации (Δqpiy), а также сила в поперечном ( x ) направлении изначально равны нулю. Используя уравнение (3), был рассчитан вектор температуры (температура каждого стержня) и, следовательно, свойства материала (зависящие от температуры) и матрицы A¯, Ax¯ и At¯. При таких условиях было определено первое значение Ny¯ с использованием уравнений (15) и (16). Затем было наложено следующее условие:
|Niy|≤Npi для i=1…n
(18)
где Npi указывает усилие текучести стержня i (зависит от температуры).Затем можно было рассчитать первое значение пластического удлинения (Δqpiy), используя предыдущее значение вектора u¯ и уравнения (11) и (14).
Затем это первое приближение пластического удлинения использовалось в (15), (16) и (18) для второго приближения вектора Ny¯, и такая процедура повторялась до достижения сходимости для рассматриваемого шага по времени.
Затем первое приближение N x было рассчитано по уравнению (17), используя значения Niy из предыдущего шага и принимая увеличение пластической деформации (Δqpix) равным нулю.
После наложения следующего условия (19) (выведенного из (13)),
[(NxdL)2+(Niydb)2−NxNiyd2Lb]0,5≤σвыход,i
(19)
и с помощью уравнения (17) было получено первое приближение члена Δqpix, которое было использовано для второго приближения N x ; это повторялось до тех пор, пока не была достигнута сходимость. Значение N x затем использовалось для определения нового значения Ny¯, и если последнее значение не было равно предыдущему (в пределах установленного допуска), N x и Δqpix пересчитывались используя последнее полученное значение Ny¯; эта итерация повторялась до достижения сходимости.
Ферро и др. [21] показали, что член, связывающий продольное напряжение с поперечным напряжением (т. е. ν N x /L ), намного меньше основного члена, Niy/b, и что поперечным напряжением больше нельзя пренебречь только ниже 300 °C, где предел текучести существенно не зависит от температуры (). Это означает, что на каждом временном шаге первое вычисленное значение N x не оказывает существенного влияния на вектор Ny¯, полученный при исходном предположении, что N x = 0, и поэтому Ny¯ ограничено только по пределу текучести материала.
Это означает, что на каждом временном шаге первое вычисленное значение N x не оказывает существенного влияния на вектор Ny¯, полученный при исходном предположении, что N x = 0, и поэтому Ny¯ ограничено только по пределу текучести материала.
Описанный алгоритм (см. также Приложение A) был написан в коде MATLAB ® . Входными данными, требуемыми программой, были геометрия инструмента (радиус штифта и буртика), скорость вращения инструмента (ω), скорость сварки (v), размер пластины (L, 2B, d), ширина канавки и общее количество стержней (n) (в данной работе b = 1 мм, а шаг по времени (Δt) задавался равным 1 с).
Учебное пособие по проектированию сварки для правильного расчета размера сварного шва и подготовки чертежа сварки для скручивающей нагрузки
Процедура расчета размера сварного шва зависит от типов нагрузки, которой подвергается сварка.Например, расчет конструкции сварки для нагрузки на чистое растяжение и расчет конструкции сварки для нагрузки изгиба отличается от расчета конструкции для нагрузки кручения. Рассмотрим расчет конструкции сварки на нагрузку кручения на примере.
Рассмотрим расчет конструкции сварки на нагрузку кручения на примере.
A Типичный пример
В приведенном выше примере вал приварен к пластине, и на вал действует чисто скручивающая нагрузка ( F) .
Данные входные данные:
Прикладные торсионные нагрузки F = 100000 N
Прочность дизайна сварки FW = 220 N / MM2
Радиус вала R = 50 мм
Желаемый выход:
Толщина сварного шва ( т) и длина участка ( с)
Процедура расчета размера сварного шва линейным методом
- Первое, что вам нужно рассчитать здесь, это крутящий момент (М).
M=F*R=5000000 Н-мм
- Рассчитайте удельную площадь проходного сечения (Au) сварного шва, как показано ниже: единица полярного момента инерции (Ju) сварного соединения, используя уравнение из стандартной таблицы и вводя значение высоты галтели ( a) = 1, как показано ниже:
J =2*pi*a*( r+0,5*a) 3
Ju =2*pi * (r+0. 5) 3 (путем нанесения a = 1)
5) 3 (путем нанесения a = 1)
= 808786.285 мм4
- Рассчитать стресс с ножным сдвигом (T) с использованием следующего уравнения:
T = M * R / Ju
= 309,1 Н/мм2
- Рассчитайте толщину шва (t) как показано ниже:
t = T/Fw
=1,4 мм
- 5 длина свариваемых участков
- , как показано ниже:
с = 1.414*t
= 1,97 мм (возьмите размер сварного шва 2 мм)
Заключение
Процедура проектирования сварки, описанная в этом руководстве по проектированию сварки, основана на BS 5950 и называется линейным методом. Высота углового шва принимается равной единице для расчета момента инерции и площади в случае линейного метода. Расчет размера сварного шва для нагрузки на кручение всегда можно проверить с помощью инструментов FEA.

 Для ДС-швов необходимо разделить величину силы на 2 (расчеты проводятся на единицу длины сварки, а не сварного шва).
Для ДС-швов необходимо разделить величину силы на 2 (расчеты проводятся на единицу длины сварки, а не сварного шва).
 Существует два способа учета влияния эффективного подводимого тепла.
Существует два способа учета влияния эффективного подводимого тепла.  5 кДж/мм — 4,0 кДж/мм
5 кДж/мм — 4,0 кДж/мм Следует учитывать, что влияние толщины листа имеет второстепенное значение при толщине листа более 60 мм из-за трехмерного теплового потока. Геометрия сварки: Влияние геометрии сварки учитывается коэффициентами геометрии сварки F 2 и F 3 для двух- и трехмерного теплового потока. Значения коэффициента геометрии шва для типовых геометрий шва:
Следует учитывать, что влияние толщины листа имеет второстепенное значение при толщине листа более 60 мм из-за трехмерного теплового потока. Геометрия сварки: Влияние геометрии сварки учитывается коэффициентами геометрии сварки F 2 и F 3 для двух- и трехмерного теплового потока. Значения коэффициента геометрии шва для типовых геометрий шва:
 Здесь можно выбрать время охлаждения, рекомендованное продуктами марки Dillinger. Как описано выше, другое время охлаждения может быть выбрано при условии, что требования к качеству свариваемой конструкции полностью выполнены и проведена соответствующая квалификация процедуры сварки. Поэтому также возможен свободный ввод времени охлаждения. В любом случае необходимо также учитывать рекомендации, приведенные в наших технических паспортах материалов.
Здесь можно выбрать время охлаждения, рекомендованное продуктами марки Dillinger. Как описано выше, другое время охлаждения может быть выбрано при условии, что требования к качеству свариваемой конструкции полностью выполнены и проведена соответствующая квалификация процедуры сварки. Поэтому также возможен свободный ввод времени охлаждения. В любом случае необходимо также учитывать рекомендации, приведенные в наших технических паспортах материалов. 0 можно.
0 можно.