Деформации и напряжения: Напряжение и деформация

Содержание

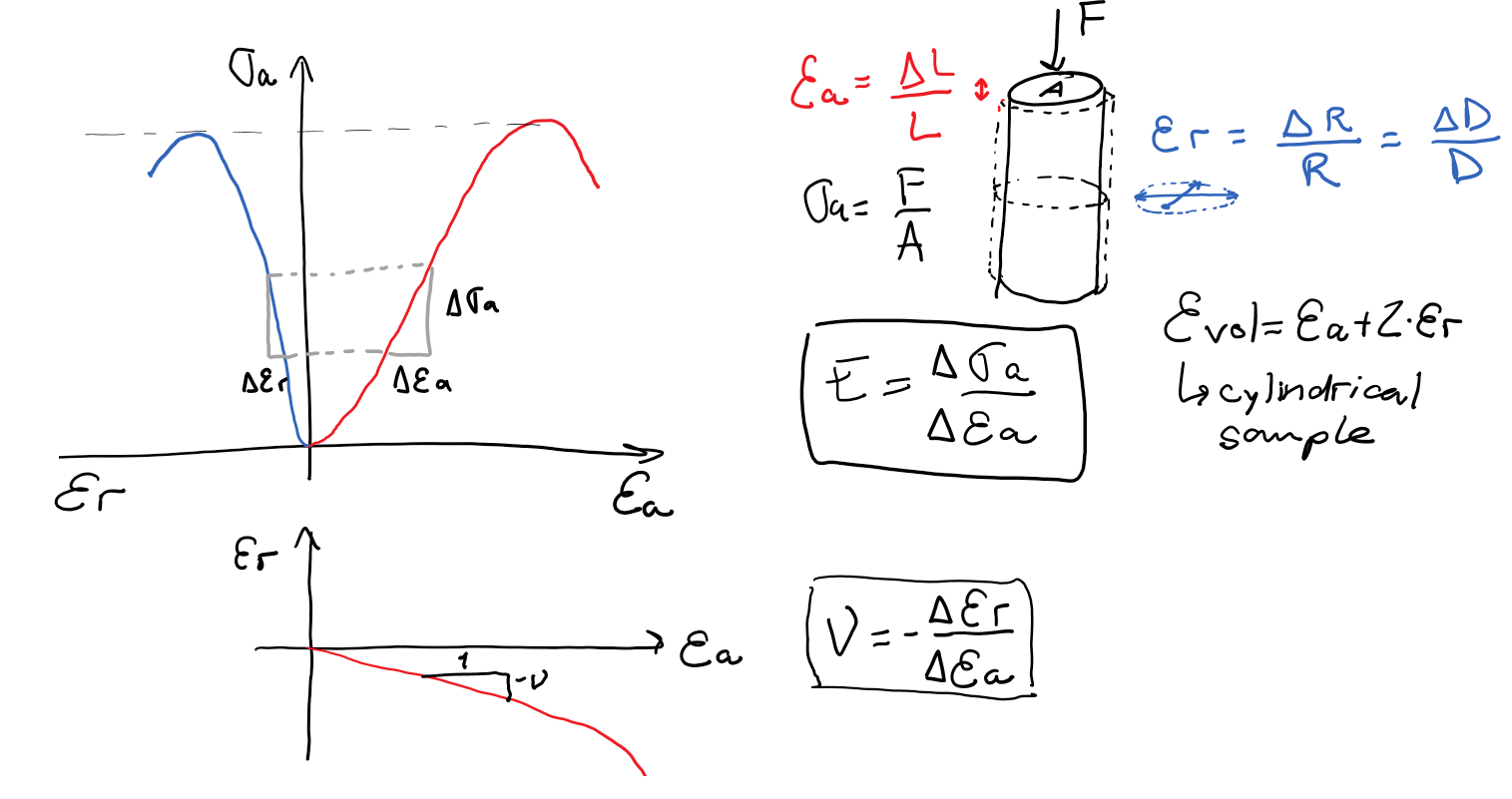
Напряжение и деформация

Для того чтобы представить себе наглядно напряжение и деформацию, следует рассмотреть натяжение стержня, изготовленного из конкретного материала. Предположим, что на стержень будет действовать сила растяжения, или растягивающая нагрузка. Под воздействием этой нагрузки стержень растянется.

stomatologicheskoe materialovedenie_1.7.1.jpg

Рис. 1.7.1. Образец материала в виде стержня растягивается в направлении продольной оси

Понятно, что если нагрузка будет слишком высокой, то стержень может разрушиться (то есть, разорваться или деформироваться). Нагрузка, при которой произойдет разрушение стержня, является мерой прочности стержня, однако не любого, а того, который имеет определенный размер и изготовлен из конкретного материала. Нагрузка, воздействие которой стержень может выдержать без разрушения, возрастет при увеличении диаметра стержня, и понизится при уменьшении его диаметра.

Длина, на которую вытянется стержень к моменту разрушения, зависит от начальной длины стержня: чем длиннее стержень до начала испытания, тем больше он вытянется. Таким образом, сила и удлинение не являются идеальными способами оценки механических свойств материала. Для того, чтобы преодолеть зависимость результата испытания от размеров испытываемого стержня, были введены такие характеристические параметры, как напряжение s, и деформация е, и им даются следующие определения: Напряжение — это сила, действующая на единицу площади поперечного сечения материала. Деформация — это изменение размера единицы длины, вызванное приложением силы.

Таким образом, если мы будем растягивать стержень, то есть, приложим к нему силу F вдоль его длины, то напряжение а может быть описано формулой:

о = F/A,

где А — площадь поперечного сечения стержня. Единицами измерения напряжения являются ньютоны на кв. метр = Н/м2 = Паскаль = Па.

В то же самое время, при воздействии на стержень силы F, длина стержня изменится от исходной длины до длины растянутого стержня. Возникшую в результате этого деформацию (относительную) можно описать формулой:

е = (L, — L0)/L0

Этот параметр будет безразмерным, поскольку при его подсчете длину делят на длину.

Существует возможность практически для любого материала измерить растяжение стержня под действием сил разной величины, и построить кривую зависимости относительной деформации от напряжения. Имея такую информацию, можно предсказать величину растяжения в зависимости от приложенной силы (нагрузки) для стержней любой длины и с любой площадью поперечного сечения. Более того, можно сравнить реакцию разных материалов на приложение одинаковых по величине растягивающих нагрузок.

Напряжение и деформация не являются свойствами материала, но они позволяют определить ряд механических свойств, которые без этих характеристических параметров невозможно было бы оценить. На выше приведенном примере напряжение возникло под воздействием продольной нагрузки (то есть, нагрузки, действующей вдоль длины стержня), однако на практике направление действия нагрузки может быть любым, и в большинстве случаев на объект будет воздействовать не одна, а несколько разных по величине нагрузок. Эти нагрузки вызывают возникновение сложных напряжений в образце.

Существует три принципиально разных типа напряжений: напряжения растяжения, сжатия и сдвига. Эти типы напряжений схематически изображены на Рис.1.7.2.

stomatologicheskoe materialovedenie_1.7.2.jpg

Рис. 1.7.2. Три основные вида напряжений: (а) растяжения; (Ь) сжатия; (с) сдвига

Клиническое значение

Нагрузка на восстановленный зуб передается через пломбу, что приводит к появлению в восстановительном материале напряжений и деформаций. Если величины этих напряжений и деформаций превышают предельные значения, которые может выдержать данный материал, то в результате может произойти его разрушение.

Определения некоторых механических свойств

Типичная кривая напряжение — деформация для металла, подобного латуни (сплаву меди с цинком), представлена на Рис. 1.7.3. Эта кривая может быть использована для оценки некоторых свойств материала.

stomatologicheskoe materialovedenie_1.7.3.jpg

Рис. 1.7.3. Кривая напряжение-деформация для пластичного (ковкого) металла (о — предел прочности при растяжении; о — прочность при разрушении; от — предел текучести; а — предел пропорциональности)

Предел упругости и пластическая деформация

Важнейшей особенностью механического поведения материалов является соотношение между напряжением и деформацией. Из Рис. 1.7.3 следует, что у латуни прямолинейная зависимость между напряжением и деформацией не сохраняется на протяжении всей кривой.

Участок кривой, где зависимость между напряжением и деформацией является линейной, известна под названием области линейной упругости. В этой об ласти наблюдается упругая деформация. При снятии напряжения в этой области, материал возвращается к своей первоначальной форме.

Место, где кривая начала отклоняться от линей ной, является точкой, в которой материал перешел через свой предел упругости, и при снятии напряжения останется деформированным, то есть не сохранит свою исходную форму. Это явление называется пластической деформацией, а область на графике — областью пластической деформации.

Основы стоматологического материаловедения
Ричард ван Нурт

Опубликовал Константин Моканов

НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ — Студопедия

Виды напряжений.Самое важное понятие в сопротивлении материалов – это понятие напряжения как силы, действующей на малую площадку и отнесенной к площади этой площадки. Напряжения бывают трех видов: растяжения, сжатия и сдвига.

Если на металлическом стержне подвешен груз, как показано на рис. 1,а, то такой стержень называется растянутым или работающим на растяжение. Напряжение σ, создаваемое силой

P в растянутом стержне с площадью поперечного сечения, равной A, дается выражением:

σ = P/A.

Если вес груза равен 50 000 Н, то растягивающая сила тоже равна 50000 Н. Далее, если ширина стержня равна 0,05 м, а толщина – 0,02 м, так что площадь поперечного сечения составляет 0,001 м², то растягивающее напряжение равно:

σ = 50 000/0,001 = 50 000 000 Н/м² = 50 МПа.

Растянутый стержень длиннее, чем до приложения растягивающих сил.

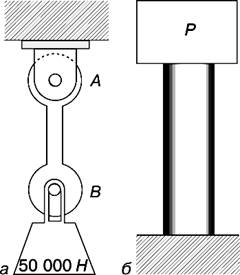
Рис. 1. РАСТЯНУТЫЙ (а) И СЖАТЫЙ (б) СТЕРЖНИ

Рассмотрим короткий цилиндр (рис. 1,б), на верхний торец которого положен груз. При этом во всех поперечных сечениях цилиндра действуют напряжения сжатия. Если напряжение равномерно распределено по всему сечению, то справедлива формула:

σ = P/A.

Сжатый цилиндр короче, чем в отсутствие деформаций.

Напряжение сдвига возникает, например, в болте (рис. 2,а), на котором верхним концом держится растянутый стержень AB с грузом 50 000 Н (рис. 1,а). Болт удерживает стержень, действуя с силой 50 000 Н, направленной вверх, на ту часть стержня, которая расположена непосредственно над отверстием в стержне, а стержень в свою очередь давит на среднюю часть болта с силой 50 000 Н. Силы, действующие на болт, приложены так, как показано на рис. 2,б. Если бы болт был сделан из материала с низким пределом прочности на сдвиг, например из свинца, то он был бы срезан по двум вертикальным плоскостям (рис. 2,в). Если же болт стальной и достаточно большого диаметра, то он не срежется, но в двух его вертикальных поперечных сечениях будут существовать напряжения сдвига. Если напряжения сдвига равномерно распределены, то они даются формулой:

τ_сд = P/A_сд.

Полная сила сдвига, действующая в каждом из поперечных сечений, равна 25 000 Н, и если диаметр болта равен 0,02 м (площадь поперечного сечения равна приблизительно 0,0003 м²), то напряжение сдвига τ_сд будет составлять 25 000 Н/0,0003 м², т.е. немногим более 80 МПа.

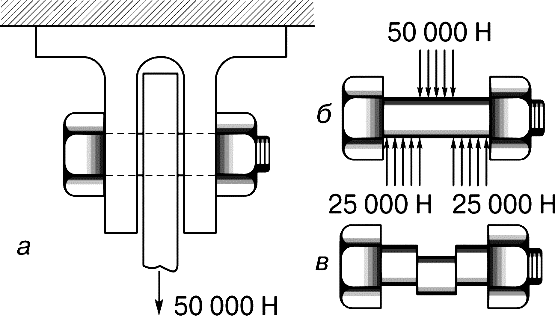
Рис. 2. НАПРЯЖЕНИЯ СДВИГА В БОЛТЕ

Напряжения растяжения и сжатия направлены по нормали (т.е. вдоль перпендикуляра) к площадке, в которой они действуют, а напряжение сдвига – параллельно площадке. Поэтому напряжения растяжения и сжатия называются нормальными, а напряжения сдвига – касательными.

Деформация.Деформацией называется изменение размера тела под действием приложенных к нему нагрузок. Деформация, отнесенная к первоначальному (до деформирования) размеру, называется относительной. Если изменение каждого малого элемента длины тела одинаково, то относительная деформация называется равномерной. Относительную деформацию часто обозначают символом e, а абсолютную (полную) – символом D. Если относительная деформация постоянна по всей длине L, то:

e = D/L.

Например, если длина стального стержня до приложения растягивающей нагрузки равна 2,00 м, а после нагружения – 2,0015 м, то полная деформация D равна 0,0015 м, а относительная – e = 0,0015/2,00 = 0,00075 (м/м).

Почти для всех материалов, применяемых в строениях и машинах, относительная деформация пропорциональна напряжению, пока оно не превысит т.н. предела пропорциональности. Это очень важное соотношение называется законом Гука. Оно было экспериментально установлено и сформулировано в 1678 году английским изобретателем и часовых дел мастером Р.Гуком. Данное соотношение между напряжением и деформацией для любого материала выражается формулой

σ = Ee,

где E – постоянный множитель, характеризующий материал. Этот множитель называют модулем Юнга по имени Т.Юнга, который ввел его в 1802 году, или же модулем упругости. Из обычных конструкционных материалов наибольший модуль упругости у стали; он равен примерно 200000 МПа. В стальном стержне относительная деформация, равная 0,00075, из приводившегося ранее примера вызывается напряжением σ = Ee = 200 000´0,00075 = 150 МПа, что меньше предела пропорциональности конструкционной стали. Если бы стержень был из алюминия с модулем упругости около 70 000 МПа, то, чтобы вызвать ту же самую деформацию 0,00075, достаточно было бы напряжения немногим более 50 МПа. Из сказанного ясно, что упругие деформации в строениях и машинах очень малы. Даже при сравнительно большом напряжении 150 МПа из приведенного выше примера относительная деформация стального стержня не превышает одной тысячной. Столь большая жесткость стали – ее ценное качество.

Чтобы наглядно представить деформацию сдвига, рассмотрим, например, прямоугольную призму ABCD (рис. 3). Ее нижний конец жестко заделан в твердое основание. Если на верхнюю часть призмы действует горизонтальная внешняя сила F, она вызывает деформацию сдвига, показанную штриховыми линиями. Смещение D есть полная деформация на длине (высоте) L. Относительная деформация сдвига g равна D/L. Для деформации сдвига тоже выполняется закон Гука при условии, что напряжение не превышает предела пропорциональности для сдвига. Следовательно, τ_s = G_sg, где G_s – модуль сдвига. Для любого материала величина G_s меньше E. Для стали она составляет около 2/5 E, т.е. приблизительно 80 000 МПа. Важный случай деформации сдвига – деформация в валах, на которые действуют внешние скручивающие моменты.

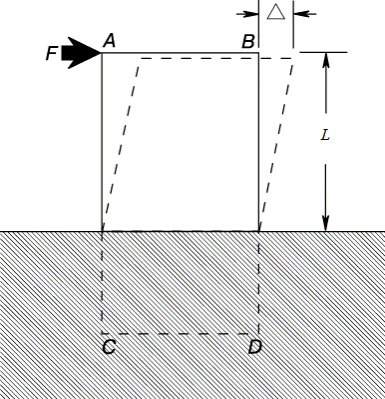
Рис. 3. ДЕФОРМАЦИЯ СДВИГА определяется как смещение Δ, отнесенное к исходной высоте L.

Выше речь шла об упругих деформациях, которые вызываются напряжениями, не превышающими предела пропорциональности. Если же напряжение выходит за предел пропорциональности, то деформация начинает расти быстрее, чем напряжение. Закон Гука перестает быть справедливым. В случае конструкционной стали в области, лежащей чуть выше предела пропорциональности, небольшое увеличение напряжения приводит к увеличению деформации во много раз по сравнению с деформацией, соответствующей пределу пропорциональности. Напряжение, при котором начинается столь быстрый рост деформации, называется пределом текучести. Материал, в котором разрушению предшествует большая неупругая деформация, называется пластичным.

Напряжение и деформация

Физика > Напряжение и деформация

Силы напряжения и деформации в физике: определение терминов, формула для модуля Юнга, движение и форма объектов, связь напряжения и деформации, уравнение.

Отношение силы к площади именуют напряжением, а отношение перемены длины к длине – деформацией.

Задача обучения

Понять, как силы влияют на форму объекта.

Основные пункты

Отношение силы к площади называют напряжением, а отношение перемены длины к длине – деформацией.
Напряжение и деформация связаны модулем Юнга (постоянная), меняющимся в зависимости от материала. Это выражается в формуле: напряжение = Y ⋅ деформацию.
Материал с высоким модулем упругости обладает высокой прочностью в растяжении. Они очень устойчивые и требуют большой силы для деформирования огромного количества.

Термины

Деформация – изменение материала под действием напряжения или силы отношения деформации к исходному размеру материала – инженерное напряжение (ϵ). Деформация определяется как естественный логарифм соотношения финальной размерности к изначальной.
Напряжение – внутреннее распределение силы на единицу площади внутри тела, реагирующего на приложенные силы, которые приводят к деформации (σ).

Сейчас мы рассмотрим силы, влияющие на движение объекта и форму. Если бульдозер вдавливает машину в стену, то транспорт не пройдет сквозь нее, а изменить свою форму. Это случается из-за присутствия силы деформации. Все знают, что даже незначительные силы вызывают неприметные деформации. При малых видно два момента: объект возвращает изначальную форму, когда сила перестает действовать и размер деформации пропорционален силе. Здесь наблюдается закон Гука: F = k ⋅ ΔL, где ΔL – изменение длины, а k – постоянная, зависящая от свойств материала.

Давайте рассмотрим виды деформации: изменение длины (растяжение и сжатие), боковой сдвиг (напряжение) и изменение объема. Ниже представлена диаграмма напряжения и деформации.

Напряжение: стержень растягивается на длину ΔL, когда сила воздействует параллельно длине. (b) Сжатие: тот же стержень сжимается силами с одинаковой величиной в противоположном направлении. При малых деформациях и однородных материалах ΔL остается практически одинаковой. В случае с большими деформациями площадь поперечного сечения меняется

Отношение силы к площади именуют напряжением, а отношение перемены длины к длине – деформацией. Напряжение и деформация связаны модулем Юнга (постоянная), изменяющимся в зависимости от материала. Модуль Юнга выражается в формуле: напряжение = Y ⋅ деформацию. Материал с высоким модулем упругости обладает высокой прочностью в растяжении. Они очень устойчивые и требуют большой силы для деформирования огромного количества.

2.2. Деформации и напряжения

быть выражено через коэффициент поперечной деформации, называемый также коэффициентом Пуассона μ:

μ = ε1/ ε.

Коэффициент Пуассона так же, как и модули упругости, является характеристикой упругих свойств материала. Все три константы упругости материала связаны между собой следующей зависимостью:

G = Е/2(1 + μ).

Наибольшее напряжение, при снятии которого остаточные деформации не превышают некоторой заданной малой величины(обычно менее

0,2 %), называют пределом упругости sУПР.

Если за участком пропорциональности напряжения и деформации следует площадка текучести, соответствующая увеличению деформации при постоянном напряжении (рис. 3.9), то это напряжение называют пределом текучести sТ. При отсутствии таковой площадки пределом текуче-

сти считают напряжение, соответствующее некоторому установленному небольшому уровню деформации (например, 0,2 %) – s0,2.

Область справедливости закона Гука устанавливаетсяпределом пропорциональности sПЦ. Поскольку пропорциональность напряжения -де формации обычно выполняется во всей области упругости, при практических расчетах предел пропорциональности принимают равным пределу упругости (или меньше).

Для использования диаграмм растяжения при других, более сложных схемах деформирования напряжениеs z заменяют интенсивностью напряжений si , а деформацию ez – интенсивностью деформаций ei .

Пластичность характеризуется относительным удлинением и относительным сужением. Относительное удлинение δ – это относительное приращение (lK – l0) расчетной длины образца после разрыва к его первоначальной расчетной длине l0, выраженное в процентах:

d = [(lK — l0 )/ l0 ]×100 %.

Относительное сужение ψ – это соотношение разности начальной и конечной площади (S0 – SK) поперечного сечения образца после разрыва к начальной площади S0 поперечного сечения, выраженное в процентах:

y = [(S0 — SK )/ S0 ]×100 %.

Испытания на растяжение не всегда оценивают склонность материала к хрупкому разрушению, поэтому применяют испытания для определения ударной вязкости, отличающиеся от обычных испытаний на растяжение тем, что образец испытывается на изгиб при ударном(динамическом) нагружении.

Ударная вязкость – способность материала сопротивляться динамическим нагрузкам, определяется как отношение затраченной на излом ра-

Понятие о напряжениях и деформациях (Лекция №5)

Как отмечалось выше, внутренние силы, действующие в некотором сечении со стороны отброшенной части тела, можно привести к главному вектору и главному моменту. Зафиксируем точку М в рассматриваемом сечении с единичным вектором нормали n. В окрестности этой точки выделим малую площадку F. Главный вектор внутренних сил, действующих на этой площадке, обозначим через P (рис. 1 а). При уменьшении размеров площадки соответственно

Рис.1. Композиция вектора напряжения.
а) вектор полного напряжения б) вектор нормального и касательного напряжений

уменьшаются главный вектор и главный момент внутренних сил, причем главный момент уменьшается в большей степени. В пределе при получим

Аналогичный предел для главного момента равен нулю. Введенный таким образом вектор р_n называется вектором напряжений в точке. Этот вектор зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки F, характеризуемой вектором п. Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора п определяет напряженное состояние в этой точке.

В общем случае направление вектора напряжений р_n не совпадает с направлением вектора нормали п. Проекция вектора р_n на направление вектора п называется нормальным напряжением , а проекция на плоскость, проходящую через точку М и ортогональную вектору n, касательным напряжением (рис. 1 б).

Размерность напряжений равна отношению размерности силы к размерности площади. В международной системе единиц СИ напряжения измеряются в паскалях: 1 Па=1 Н/м².

При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.

Отнесем недеформированное тело к декартовой системекоординат Oxyz (рис. 2). Положение некоторой точки М в этой системе координат определяется радиус-вектором r(х, у, z). В деформированном состоянии точка М займет новое положение М^/ , характеризуемое радиус-вектором r‘ (х, у, z). Вектор u=r’r называется вектором, перемещений точки М. Проекции вектора u на координатные оси определяют компоненты вектора перемещений и(х, у, z), v(х, у, z), w(х, у, z), равные разности декартовых координат точки тела после и до деформации.

Перемещение, при котором взаимное расположение точек тела не меняется, не сопровождается деформациями. В этом случае говорят, что тело перемещается как жесткоецелое (линейное перемещение в пространстве или поворот относительно некоторой точки). С другой стороны, деформация, связанная с изменением формы тела и его объема, невозможна без перемещения его точек.

Рис.2. Композиция вектора перемещения

Деформации тела характеризуются изменением взаимного расположения точек тела до и после деформации. Рассмотрим, например, точку М и близкую к ней точку N, расстояние между которыми в недеформированном состоянии вдоль направления вектора s обозначим через (рис. 2). В деформированном состоянии точки М и N переместятся в новое положение (точки М’ и N), расстояние между которыми обозначим через s’. Предел отношения

называется относительной линейной деформацией в точке М в направлении вектора s, рис.3. Рассматривая три взаимно перпендикулярных направления, например, вдоль координатных осей Ох, Оу и Oz, получим три компоненты относительных линейных деформаций характеризующих изменение объема тела в процессе деформации.

Для описания деформаций, связанных с изменением формы тела, рассмотрим точку М и две близкие к ней точки N и Р, расположенные в недеформированном состоянии в направлении двух взаимно ортогональных векторов s₁ и s₂. Расстояния между точками обозначим через и (рис. 4). В деформированном состоянии положение точек обозначим через М’, N’ и Р’. Угол между отрезками M’N’ и М’Р’ в общем случае будет отличным от прямого. При , изменение угла между двумя ортогональными до деформации направлениями называется угловой деформацией. Как видно из рис. 4, угловая деформация складывается из двух углов и , связанных с поворотами отрезков MN’ и М’Р’ ‘в.плоскости, образованной векторами s₁ и s₂, относительно этих векторов. Если заданы три взаимно ортогональных вектора, направленных вдоль координатных осей, то имеются три угловые деформации , и , которые вместе с тремя линейными деформациями , и полностью определяют деформированное состояние в точке.

Рис.3. Композиция линейной деформации

Рис. 4. Композиция угловой деформации

НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ. ТЕНЗОР НАПРЯЖЕНИЙ
   Вектор напряжений p_n является физическим объектом, имеющим длину, направление и точку приложения. В этом смысле он обладает векторными свойствами. Однако этому объекту присущи некоторые свойства, не характерные для векторов. В частности, величина и направление вектора напряжений зависят от ориентации вектора n нормали бесконечно малого элемента поверхности dF. Совокупность всех возможных пар векторов п, р_n в точке определяет напряженное состояние в данной точке. Однако для полного описания напряженного состояния в точке нет необходимости задавать бесконечное множество направлений вектора n, достаточно определить векторы напряжений на трех взаимно перпендикулярных элементарных площадках. Напряжения на произвольно ориентированных площадках могут быть выражены через эти три вектора напряжений. В дальнейшем лектор умышленно меняет ориентацию координат. Так, что ось Z продольная ось бруса, а X и Y координаты любой точки его поперечного сечения.
   Проведем через точку М три взаимно перпендикулярных плоскости с векторами нормалей, направления которых совпадают с направлениями координатных осей. Элементарные площадки образуем дополнительными сечениями, параллельными исходным плоскостям и отстоящими от них на бесконечно малые расстояния dx, dy, dz. В результате в окрестности точки М получим бесконечно малый параллелепипед, поверхность которого образована элементарными площадками dF_х=dydz, dF_н==dxdz, dF_я=dxdy. Векторы напряжений p_x, p_y, p_z, действующие на элементарных площадках, показаны на рис. 5.
   Разложим каждый вектор напряжений на составляющие вдоль координатных осей (рис. 6). На каждой площадке действует одно нормальное напряжение , , , где индекс обозначает направление вектора нормали к площадке и два касательных напряжения с двумя индексами, из которых первый указывает направление действия компоненты напряжения, второйнаправление вектора нормали к площадке.
Рис. 5. Равновесное состояние бесконечно-малого параллелепипеда

Рис.6. Компоненты тензора напряженного состояния

   Совокупность девяти компонент напряжений (по три на каждой из трех взаимно перпендикулярных площадок) представляет собой некоторый физический объект, называемый тензором напряжений в точке. Тензор можно представить в виде матрицы, соответствующим образом упорядочив девять компонент:
   Для компонент тензора напряжений общепринятым является следующее правило знаков: компонента считается положительной, если на площадке с положительной внешней нормалью (т. е. направленной вдоль одной из координатных осей) эта компонента направлена в сторону положительного направления соответствующей оси. На рис. 6 все компоненты тензора напряжений изображены положительными. На площадках с отрицательной внешней нормалью (грани параллелепипеда, не видимые на рис. 5 и 6) положительная компонента направлена в противоположном направлении. Напряжения на трех взаимно ортогональных площадках с отрицательными направлениями нормалей также характеризуют напряженное состояние в точке. Эти напряжения, являющиеся компонентами тензора напряжений, определяются аналогично напряжениям на площадках с положительной нормалью. Они обозначаются теми же символами и имеют положительное направление, обратное изображенному на рис. 6.
Дальше…
Сопротивление материалов. Шпаргалка для студентов (Р. Н. Сиренко, 2009)
3. Понятие о деформациях и напряжениях
Воздействие на тело внешних сил изменяет его внутренние силы. Деформация тела вызывает изменение расстояний между атомами, при этом возникающие дополнительные внутренние силы стремятся вернуть тело в первоначальное положение. Если неограниченно увеличивать действие внешних сил, то при определенном возрастании внутренних сил происходит разрушение тела. Чтобы произвести расчет на прочность, надо уметь определять внутренние силы, зная внешние. Для определения внутренних сил (или внутренних силовых факторов) используют метод сечения. Мысленно рассекаем твердое тело и отбрасываем одну из частей. Оставшаяся часть тела находится в положении равновесия под действием приложенных внешних сил и сил, приложенных к сечению (заменяющих воздействие отброшенной части тела). Теперь при помощи теоретической физики можно определить главный вектор действия внутренних сил по сечению (закон распределения этих сил установить сложно). Совмещая плоскость сечения с системой координат, имеем в сечении шесть силовых факторов: продольная сила N_z, пара поперечных сил Q_x,Q_y, изгибающие моменты M_x,M_y, крутящий момент M_z.
Соответственно видам внутренних силовых факторов различают четыре вида деформаций тела:
– если в сечении имеется только продольная сила – растяжение или сжатие;
– если в сечении возникают только поперечные силы – сдвиг;
– если в сечении возникают только изгибающие моменты – чистый изгиб, если кроме изгибающих моментов возникают поперечные силы – поперечный изгиб;
– если в сечении возникает крутящий момент – кручение.
Если в сечении действуют несколько силовых факторов, то возникает сложный вид деформации.
Как уже было сказано, при определении внутренних сил методом сечения считаем эти силы приложенными к центру тяжести сечения. На самом деле они распределены по всей поверхности сечения, и интенсивность внутренних силовых факторов может быть различной. Увеличение внешней нагрузки приводит к увеличению внутренней, заставляет возрастать интенсивность во всех точках сечения и может привести к разрушению элемента или возникновению остаточных деформаций. Таким образом, говоря о прочности тела, рассматривать надо не значение внутренних сил, а их интенсивность. Меру интенсивности внутренних сил характеризует напряжение. Для удобства математического и физического анализа напряжение рассматривают как совокупность двух компонент: вектора нормального напряжения и вектора касательно напряжения, являющихся соответственно его составляющими по нормали к сечению и касательно к его плоскости.
Деформации и напряжения — Студопедия
Напряжение – мера внутренних сил, возникающих в материале под влиянием внешних воздействий (нагрузок, изменения температуры и пр.). Для изучения напряжений через произвольную точку тела мысленно проводится сечение (рис. 3.1) и отбрасывается одна из половин тела. Действие отброшенной половины на другую половину заменяют внутренними силами.
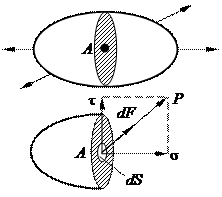
Рис. 3.1. Схема замены внешних сил на внутренние напряжения
В малом элементе сечения площадью dS в окрестности произвольной точки А действует произвольно направленная внутренняя сила dF.
Отношение р = dF/dS называется вектором напряжения в точке А по площадке dS. Составляющие вектора напряжения, действующие по нормали к площадке, обозначаются σ и называются нормальными напряжениями, а действующие вдоль площадки называются касательными напряжениями τ в точке А по площадке dS, причём σ² + τ² = р².
В общем случае напряженное состояние тела в точке А характеризуется совокупностью всех векторов напряжений для всевозможных сечений (площадок, проходящих через точку А), а значит и для любого направления. Напряженное состояние в точке А может быть определено с помощью тензора напряжений и характеризуется девятью компонентами по трем осям координат (три нормальных и шесть касательных). Касательные напряжения попарно равны (τ_ху = τ_ух, τ_хz = τ_zх, τ_уz = τ_zу), т. е. остается всего шесть компонентов. Напряжения выражаются в Па (паскалях).
Т_н = 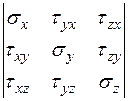. (3.1)
Для тензора характерным является закон, по которому преобразуется его компоненты при повороте осей координат. При повороте системы координат можно отыскать такое ее положение, когда касательные напряжения будут равны нулю. Эти направления называют главными.

Главные направления тензора напряжений определяются условием, зависящим от трех инвариантов I₁, I₂, I₃ .
Первым инвариантом I₁ тензора напряжений является сумма нормальных напряжений:
I₁ = σ_х+ σ_у+ σ_z = 3σ₀. (3.2)
Среднее значение трёх нормальных напряжений называют гидростатическим давлением:
σ₀= (σ_х+ σ_у+ σ_z)/3. (3.3)
Гидростатическому давлению соответствует тензор напряжений, нормальные компоненты которого равны σ₀, а касательные – нулю. Поскольку гидростатическое давление не вызывает в металле пластических деформаций, его исключают из системы напряжений. Оставшуюся часть тензора называют девиатором напряжений S_σ:

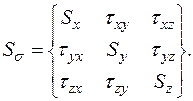(3.4)
Второй инвариант I₂ тензора напряжений определяется следующим выражением:
I₂ = σ_хσ_у+ σ_х σ_z + σ_уσ_z – τ²_ху – τ²_уz – τ²_zх. (3.5)
Величины, пропорциональные корню квадратному из второго инварианта девиатора напряжений, называют интенсивностью касательных напряжений τ_i и интенсивностью нормальных напряжений σ_i:
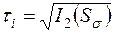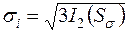, . (3.6)
Напряжения в материале могут возникнуть при физико-химических процессах, при неравномерном распределении температуры (при нагреве и охлаждении металла), а также вследствие фазовых превращений при термической обработке. При этом напряжения, возникающие в объеме всего тела, называют макронапряжениями (или напряжениями Ι рода), а напряжения, возникающие в объеме одного зерна, называют микронапряжениями (или напряжениями ΙΙ рода). Напряжения, возникающие в объемах порядка нескольких параметров кристаллической решетки, называются субмикроскопическими (или напряжениями ΙΙΙ рода). Деформациями называют изменения формы или размеров тела (или части тела) под действием внешних сил, а также при нагревании или охлаждении и других воздействиях, вызывающих изменение относительного положения частиц тела (рис. 3.2).
Рис. 3.2. Схема деформации: а) линейная деформация, б) угловая деформация
С геометрической точки зрения деформированное состояние в точке описывается тензором деформации:
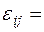
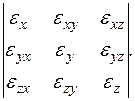(3.7)
Компоненты 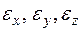, характеризуют линейные деформации волокон, расположенных по осям x, y, z: относительные удлинения (или относительные укорочения), а компоненты 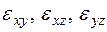– углы поворота двух взаимно перпендикулярных до деформации волокон (или деформации сдвига).
Для компонент деформаций сдвига справедливы равенства:
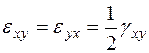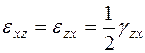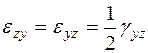, , . (3.8)
При повороте системы координат все компоненты тензора деформации преобразуются по определенным линейным относительно направляющих косинусов соотношениям. В теории деформации и линейных преобразований доказывается, что из всех возможных направлений осей координат существует тройка взаимно перпендикулярных направлений (главных направлений), относительно которых все сдвиговые компоненты деформации равны нулю. Главные направления деформаций определяются тремя скалярными величинами, не зависящими от положения системы координат и поэтому называемыми инвариантами.
Первый инвариант 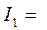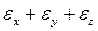используется для записи условия постоянства объема деформируемого металла:
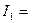
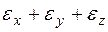= 0. (3.9)
Второй инвариант тензора деформации имеет вид:
I₂= 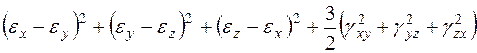. (3.10)
Величина, пропорциональная корню квадратному из второго инварианта, называется интенсивностью деформаций и используется для характеристики деформаций в общем случае деформированного состояния.
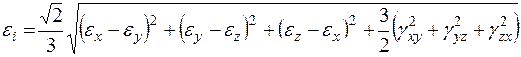. (3.11)
Простейшие схемы деформирования – растяжение, сжатие, сдвиг, кручение, изгиб. Первые две схемы (растяжение и сжатие) могут быть описаны только линейными компонентами, вторые (сдвиг, кручение, изгиб) – только сдвиговыми (угловыми).
Основные напряжения и деформации
Введение
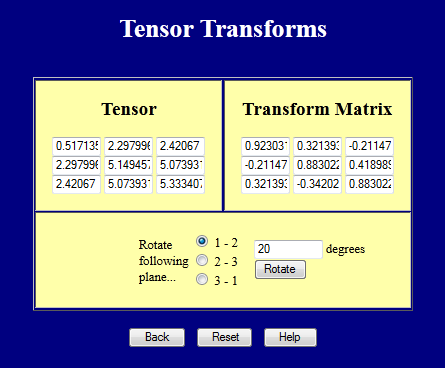
Эта страница охватывает основные стрессы и напряжения. Хотя мы еще не обсуждали много разных определений стресса и напряжения, на самом деле верно то, что все, что здесь обсуждается, применяется независимо от типа тензор напряжения или деформации. Например, если вы рассчитываете основные значения тензор напряжений Коши, то, что вы получите, это главные напряжения Коши. главными значениями тензора деформации Грина будут главные деформации Грина.Т \) в 2-м. Они также могут быть получены из баланса сил фигуры, показанной здесь. Интересно, что стресс характеризуется как тензор, потому что он следует уравнению преобразования. Но это в первую очередь математический аргумент, и он имел бы небольшой вес, если бы не был связан с физикой баланса сил. Дело в том, что уравнение преобразования координат должным образом отражает баланс сил в различных ориентациях, что делает его актуальным.
Основными напряжениями являются соответствующие нормальные напряжения под углом \ (\ theta_P \), при котором напряжение сдвига, \ (\ tau ‘_ {xy} \), это ноль.
Эта страница выполняет полный трехмерный тензор прообразы, но все еще можно использовать для двумерных задач .. Введите значения в верхнем левом положении 2×2 и поверните в плоскости 1-2, чтобы выполнить преобразования в 2-D. На скриншоте ниже показан случай чистого сдвига повернут на 45 ° для получения главных напряжений. Обратите также внимание на то, как матрица \ ({\ bf Q} \) прообразы.

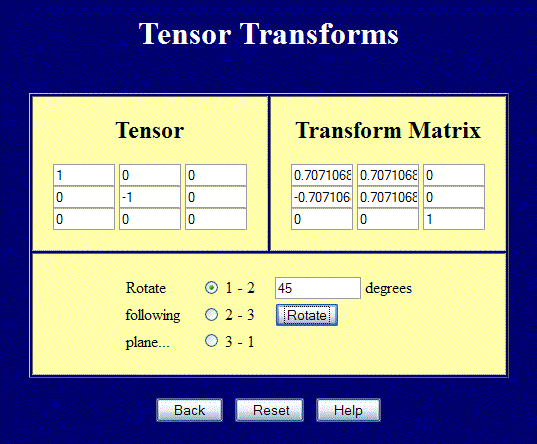
На рисунке ниже показаны напряжения, соответствующие случаю чистого сдвига в тензоре Пример преобразования веб-страницы. Выровненный по осям синий квадрат явно подвергается сдвигу.Но красный квадрат, вписанный в больший синий квадрат, видит только простое напряжение и сжатие. Это основные значения случая чистого сдвига в глобальной системе координат.
В 2-D, ориентация основного напряжения, \ (\ theta_P \), может быть вычислена путем установки \ (\ tau ‘\! _ {xy} = 0 \) в приведенном выше уравнении сдвига и решение для \ (\ theta \) чтобы получить \ (\ theta_P \), угол основного напряжения.
\ [ 0 = (\ sigma_ {yy} — \ sigma_ {xx}) \ sin \ theta_P \ cos \ theta_P + \ tau_ {xy} (\ cos ^ 2 \ theta_P — \ sin ^ 2 \ theta_P) \]
Это дает
\ [ \ tan (2 \ theta_P) \; знак равно {2 \ tau_ {xy} \ over \ sigma_ {xx} — \ sigma_ {yy}} \]
Матрица преобразования \ ({\ bf Q} \)
\ [ {\ bf Q} = \ left [\ matrix { \; \; \; \ cos \ theta_P & \ sin \ theta_P \\ — \ sin \ theta_P & \ cos \ theta_P } \право] \]
Вставка этого значения для \ (\ theta_P \) обратно в уравнения для нормальных напряжений дает основные ценности.Т \) с \ ({\ bf Q} \) на основе \ (\ theta_P \).
Основная стрессовая нотация
Основные напряжения можно записать как \ (\ sigma_1 \), \ (\ sigma_2 \), и \ (\ sigma_3 \). В этом случае обычно используется только один индекс дифференцировать значения основного напряжения от компонентов нормального напряжения: \ (\ sigma_ {11} \), \ (\ sigma_ {22} \) и \ (\ sigma_ {33} \).
Пример 2-D основного стресса
Начнем с тензора напряжений
\ [ \ boldsymbol {\ sigma} = \ left [\ matrix { 50 & \; \; \; 30 \\ 30 & -20 } \право] \]
Основная ориентация
\ [ \ Начать {eqnarray} \ tan (2 \ theta_P) & = & {2 * 30 \ свыше 50 — (\ text {-} 20)} \\ \\ \\ \ theta_P & = & 20.\ circ)} \право] \\ \\ \\ знак равно \осталось[ \ matrix {61.1 & \; \; \; 0.0 \\ 0.0 & -31.1} \право] \ Конец {eqnarray} \]
Это подтверждает, что значение основного напряжения 61,1 в слоте \ (\ sigma_ {11} \) действительно 20,3 ° от оси X. Значение \ (\ sigma_ {22} \) 90 ° от первого.
3-D Основные Напряжения
Координаты преобразования в 3-D
\ [ \осталось[ \ matrix {\ sigma ‘_ {11} & \ sigma’ _ {12} & \ sigma ‘_ {13} \\ \ sigma ‘_ {12} & \ sigma’ _ {22} & \ sigma ‘_ {23} \\ \ sigma ‘_ {13} & \ sigma’ _ {23} & \ sigma ‘_ {33}} \ right] = \осталось[ \ matrix {q_ {11} & q_ {12} & q_ {13} \\ q_ {21} & q_ {22} & q_ {23} \\ q_ {31} & q_ {32} & q_ {33}} \право] \осталось[ \ matrix {\ sigma_ {11} & \ sigma_ {12} & \ sigma_ {13} \\ \ sigma_ {12} & \ sigma_ {22} & \ sigma_ {23} \\ \ sigma_ {13} & \ sigma_ {23} & \ sigma_ {33}} \право] \осталось[ \ matrix {q_ {11} & q_ {21} & q_ {31} \\ q_ {12} & q_ {22} & q_ {32} \\ q_ {13} & q_ {23} & q_ {33}} \право] \]
Вторая матрица \ ({\ bf Q} \) — это еще раз транспонирование первой.
Эта страница выполняет тензорные преобразования.

И эта страница вычисляет основные значения (собственные значения) и главные направления (собственные векторы).

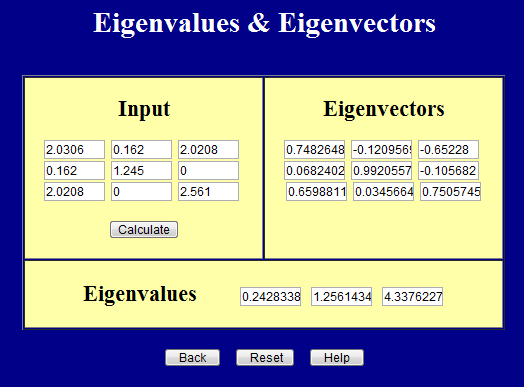
Важно помнить, что входные данные для обеих страниц должны быть симметричными. По факту, обе страницы обеспечивают это.
Собственные значения выше могут быть записаны в виде матрицы в виде
\ [ \ boldsymbol {\ sigma} = \ left [\ matrix { 24 & 0 & 0 \\ 0 & 125 & 0 \\ 0 & 0 & 433} \право] \]
Максимальное напряжение сдвига
Максимальное напряжение сдвига в любой точке легко рассчитать по Основные стрессы.Это просто
\ [ \ tau_ {max} = {\ sigma_ {max} — \ sigma_ {min} \ over 2} \]
Это относится как к 2-му и 3-му. Максимальный сдвиг всегда происходит в ориентация системы координат, повернутая на 45 ° от основного система координат. Для основного тензора напряжений выше
\ [ \ boldsymbol {\ sigma} = \ left [\ matrix { 24 & 0 & 0 \\ 0 & 125 & 0 \\ 0 & 0 & 433 } \право] \]
Максимальное и минимальное главные напряжения находятся в слотах \ (\ sigma_ {33} \) и \ (\ sigma_ {11} \), соответственно.Таким образом, максимальная ориентация сдвига получается путем вращения главная система координат на 45 ° в плоскости (\ (1-3 \)).
Само максимальное значение сдвига
\ [ \ Начать {eqnarray} \ tau_ {max} & = & {\ sigma_ {max} — \ sigma_ {min} \ over 2} \\ \\ & = & (433 — 24) / 2 \\ \\ & = & 204 \ Конец {eqnarray} \]
2-D Основные Штаммы
Механизм вычисления главных напряжений идентичен механизму вычисления главных напряжений.2 \ тета) \ Конец {eqnarray} \]
Уравнения записаны в терминах \ (\ gamma / 2 \), чтобы подчеркнуть, что половина всех значения сдвига используются в уравнениях преобразования.
Эта страница выполняет полное трехмерное тензорное преобразование, но все еще можно использовать для двумерных задач .. Введите значения в верхнем левом положении 2×2 и поверните в плоскости 1-2, чтобы выполнить преобразования в 2-D. На скриншоте ниже показан случай чистого сдвига повернут на 45 °, чтобы получить основные штаммы. Обратите также внимание на то, как матрица \ ({\ bf Q} \) прообразы.

На рисунке ниже показаны деформированные формы, соответствующие случаю чистого сдвига в тензоре Пример преобразования веб-страницы. Выровненный по осям синий квадрат явно подвергается сдвигу. Но красный квадрат, вписанный в больший синий квадрат, видит только простое напряжение и сжатие. Это основные значения чистой деформации сдвига в глобальной системе координат.
В 2-D, ориентация основного напряжения, \ (\ theta_P \), может быть вычислена путем установки \ (\ gamma ‘\! _ {xy} = 0 \) в приведенном выше уравнении сдвига и решение для \ (\ theta \) чтобы получить \ (\ theta_P \), главный угол деформации.2 \ theta_P) \]
Это дает
\ [ \ tan (2 \ theta_P) \; знак равно {\ gamma_ {xy} \ over \ epsilon_ {xx} — \ epsilon_ {yy}} \; знак равно {2 \ epsilon_ {xy} \ over \ epsilon_ {xx} — \ epsilon_ {yy}} \]
Матрица преобразования \ ({\ bf Q} \)
\ [ {\ bf Q} = \ left [\ matrix { \; \; \; \ cos \ theta_P & \ sin \ theta_P \\ — \ sin \ theta_P & \ cos \ theta_P } \право] \]
Вставка этого значения для \ (\ theta_P \) обратно в уравнения для нормальных деформаций дает основные ценности. Они пишутся как \ (\ epsilon_ {max} \) и \ (\ epsilon_ {min} \), или как \ (\ epsilon_1 \) и \ (\ epsilon_2 \).Т \) с \ ({\ bf Q} \) на основе \ (\ theta_P \).
Нотация основного штамма
Основные штаммы могут быть записаны как \ (\ epsilon_1 \), \ (\ epsilon_2 \), и \ (\ epsilon_3 \). В этом случае обычно используется только один индекс дифференцировать основные значения деформации от нормальных компонентов деформации: \ (\ epsilon_ {11} \), \ (\ epsilon_ {22} \) и \ (\ epsilon_ {33} \).
Пример 2-D основного штамма
Начнем с тензора деформации
\ [ \ boldsymbol {\ epsilon} = \ left [\ matrix { 0.\ circ)} \право] \\ \\ \\ знак равно \осталось[ \ matrix {0.611 & \; \; \; 0.000 \\ 0,000 & -0,311} \право] \ Конец {eqnarray} \]
Это подтверждает, что значение основного напряжения 0,611 в \ (\ epsilon_ {11} \) слот действительно 20,3 ° от оси X. Значение \ (\ epsilon_ {22} \) 90 ° от первого.
3-D Основные штаммы
Координаты преобразования в 3-D
\ [ \осталось[ \ matrix {E ‘_ {11} & E’ _ {12} & E ‘_ {13} \\ E ‘_ {12} & E’ _ {22} & E ‘_ {23} \\ E ‘_ {13} & E’ _ {23} & E ‘_ {33}} \ right] = \осталось[ \ matrix {q_ {11} & q_ {12} & q_ {13} \\ q_ {21} & q_ {22} & q_ {23} \\ q_ {31} & q_ {32} & q_ {33}} \право] \осталось[ \ matrix {E_ {11} & E_ {12} & E_ {13} \\ E_ {12} & E_ {22} & E_ {23} \\ E_ {13} & E_ {23} & E_ {33}} \право] \осталось[ \ matrix {q_ {11} & q_ {21} & q_ {31} \\ q_ {12} & q_ {22} & q_ {32} \\ q_ {13} & q_ {23} & q_ {33}} \право] \]
Вторая матрица \ ({\ bf Q} \) — это еще раз транспонирование первой.
Эта страница выполняет тензорные преобразования.

И эта страница вычисляет основные значения (собственные значения) и главные направления (собственные векторы).

Важно помнить, что входные данные для обеих страниц должны быть симметричными. По факту, обе страницы обеспечивают это.
Собственные значения выше могут быть записаны в виде матрицы в виде
\ [ {\ bf E} = \ left [\ matrix { 0,243 & 0 & 0 \\ 0 & 1.256 & 0 \\ 0 & 0 & 4.338 } \право] \]
Максимальный сдвиг
Максимальное количество сдвига в любой точке легко рассчитать по Основные штаммы. Это просто
\ [ \ gamma_ {max} = \ epsilon_ {max} — \ epsilon_ {min} \]
Это относится как к 2-му и 3-му. Максимальный сдвиг всегда происходит в ориентация системы координат, повернутая на 45 ° от основного система координат. Для основного тензора деформации выше
\ [ {\ bf E} = \ left [\ matrix { 0,243 & 0 & 0 \\ 0 & 1.256 & 0 \\ 0 & 0 & 4.338 } \право] \]
Максимальные и минимальные главные деформации находятся в \ (E_ {33} \) и \ (E_ {11} \) слотах, соответственно. Таким образом, максимальная ориентация сдвига получается путем вращения главная система координат на 45 ° в плоскости (\ (1-3 \)).
Само максимальное значение сдвига
\ [ \ Начать {eqnarray} \ gamma_ {max} & = & \ epsilon_ {max} — \ epsilon_ {min} \\ \\ & = & 4.338 — 0.243 \\ \\ & = & 4.095 \ Конец {eqnarray} \]
Резюме
Этот принцип инвариантных величин при преобразованиях координат фактически универсален для всех матриц, которые симметричны и преобразуются в соответствии с
\ [ {\ bf A} ‘= {\ bf Q} \ cdot {\ bf A} \ cdot {\ bf Q} ^ T \]
где \ ({\ bf A} \) — «любая симметричная матрица.Т \! \ cdot {\ bf F} \) для резины всегда равно 1, потому что резина несжимаема. Так что это не только константа, не зависит от преобразования координат, но это даже постоянное значение, всегда равно 1, независимо от преобразования координат и состояния деформации.
учебников
,
стресс и напряжение

Количественные понятия: тригонометрия, построение графиков
^{д-р Кэрол Орманд (Университет Висконсин — Мэдисон) и д-р Эрик Баер (Highline Community College)}
Перейти к: Напряжение, напряжение и усиление; сооружения | Условия деформации | Недостатки | Аналоги | Примеры обучения | Ресурсы
основных концепций
Есть 5 основных понятий, с которыми студенты борются, когда думают о стрессе и напряжении:
породы деформируются,
стресс вызывает деформацию и приводит к деформации в структурах,
разные физические условия создают разные структуры,
вывод стресса от неисправностей, и
связь между аналогами и реальностью.
Скалы деформируют
Многим студентам трудно понять, что камни могут гнуться или ломаться. У них также могут возникнуть трудности с представлением сил, необходимых для складывания или разрушения горных пород, или понимания того, что внешне постоянная Земля может значительно измениться со временем. Это особенно верно в отношении студентов, которые живут в тектонически устойчивых районах. Если студенты хотят понять основы стресса и напряжения, они должны преодолеть этот барьер, так как будет трудно исследовать причины и условия деформации, если студенты не могут понять деформацию.Часто бывает полезно, чтобы учащиеся создавали аналоговые модели структур, представленных на фотографиях из камней или на образцах рук.
Вот изображение структуры, известной как будинаж (названной в честь французского слова «кровяная колбаса» — обратите внимание на структуру, похожую на колбасу). Можете ли вы сделать аналогичную структуру, используя свою Silly Putty®? Какая скорость деформации необходима для получения чего-то подобного (вы получите тот же результат, если вы разложите это быстро или медленнее)? Работает ли лучше, если ваша Silly Putty® теплая или холодная? Как вы думаете, тот же результат будет с PlayDoh® или тестом для печенья? Влияет ли количество Silly Putty® на то, насколько легко вы можете воспроизвести структуру? Все эти условия могут быть переведены в горные породы — скорость, с которой они напряжены, температура, тип материала, масштаб — и влияют на типы структур, которые отображаются в записи горных пород.
Для того, чтобы показать студентам, что породы деформируются, можно использовать фотографии и образцы рук реальных разломанных и сложенных камней в различных масштабах. Существует несколько хороших коллекций этих типов изображений, таких как Всемирный банк изображений AGI Earthscience, коллекция Мартина Миллера или набор слайдов с ошибками Национального центра геофизических данных.
Стресс вызывает напряжение, напряжение приводит к структурам
Многие геологи считают, что начинающим студентам важно понимать, что видимые структуры — это запись стресса и физических условий на Земле.В результате различия между напряжением, деформацией и структурами, сформированными во время деформации, становятся ключевыми понятиями.
Стресс — сила, действующая на камень на единицу площади. Он имеет те же единицы измерения, что и давление, но также имеет направление (то есть это вектор, как и сила). Существует три типа напряжения: сжатие, растяжение и сдвиг. Стресс может вызвать напряжение, если этого достаточно для преодоления силы объекта, находящегося в состоянии стресса.
Штамм — это изменение формы или размера в результате приложенных сил (деформации).Скалы только напрягаются, когда находятся под напряжением. Любой камень может быть напряженным. Штамм может быть упругим, ломким или пластичным. Пластичная деформация также называется пластической деформацией.
Структуры в геологии являются признаками деформации, возникающими в результате постоянного (хрупкого или пластичного) напряжения. Примеры включают складки и разломы. Геологи используют эти функции для определения типа стресса, который испытал камень, а также условий стресса, которым он подвергался (или испытывал удовольствие, в зависимости от вашей точки зрения).
После показа изображений деформированных камней, предоставляя учащимся возможность создавать свои собственные «конструкции» с помощью Play-Doh®, Silly Putty® или другой геологический аналоговый материал помогает им понять концепции, которые лежат в основе напряжения и деформации, и позволяет им исследовать взаимосвязи между напряжением, деформацией и деформационными структурами. Студенты могут экспериментировать с типами напряжения и уровнями напряжения, необходимыми для того, чтобы аналоги сломались или погнулись. Альтернативно, они могут использовать структуры в аналоге для определения напряжений и скоростей деформации после создания «структуры».См. Скалы деформируют выше для примера того, как студенты создают будины.
Стресс, напряжение и структура начинаются с одних и тех же трех букв, но означают совершенно разные вещи. Эти слова также используются в геологии иначе, чем в английском, что может вызвать путаницу. Тем не менее, вот некоторые уловки, которые я использую, чтобы запомнить:
Стресс такой же, как давление. Когда вы находитесь под давлением, вы находитесь в состоянии стресса!
Стресс может произойти без напряжения, но напряжение не может произойти без стресса.
Посмотри на этот камень, который я сжимаю в руке.
Это подчеркнуто? (Да, это под давлением.)
Это напрягается? (Нет, это не изменило форму.)
Теперь посмотрите на этот камень со складкой.
Это под стрессом? (Нет, это не под давлением).
Это напрягает? (Нет, в настоящее время он не меняет форму.)
Есть ли у него структура? (Да, есть складка.)
В дополнение к Silly Putty® и Play-Doh®, деревянные блоки с нанесенными слоями или бак для сжатия / сжатия, заполненный слоистым песком или хлопьями для завтрака, также хорошо моделирует конструктивные особенности.Аналоги, однако, трудно масштабировать надлежащим образом (как во времени, так и в пространстве) с гигантскими масштабами, в которых формируются геологические структуры. У студентов все еще могут быть трудности с пониманием огромного масштаба сил, необходимых для изгибания или разрушения камня, и длительных временных масштабов, необходимых для создания структур. Убедитесь, что вы даете понять своим студентам, что эти подводные камни существуют. Более подробные идеи для аналогов доступны на веб-странице материалов для преподавания структурной геологии.
После того, как учащиеся освоили связь между стрессом, деформацией и структурой, я разработал таблицу 3 x 2 различных структур, которые формируются в различных условиях стресса и деформации.Затем я приступаю к заполнению таблицы с помощью студентов.
Давайте посмотрим, какие особенности обнаруживаются в разных стрессовых условиях и при разных стилях напряжения. Мы сделаем это, сделав стол. Каковы три типа стресса? Сжатие, напряжение и сдвиг. Теперь, каковы 2 типа постоянной деформации? Пластичный и ломкий. Давайте создадим таблицу размером три столбца на две строки и заполните ее соответствующими структурами! Когда мы закончим, у нас должно быть 6 видов деформаций.

Теперь посмотрим, сможете ли вы сделать каждый из них с помощью Play-Doh® или блоков.
Различные условия приводят к различным стилям деформации
Существует множество факторов, влияющих на стиль деформации в породе, включая давление, температуру, состав породы, наличие или отсутствие флюидов, тип напряжения, скорость напряжения и другие. Тем не менее, тип стресса, уровень стресса и температура могут быть наиболее важными факторами для большинства вводных студентов.
Silly Putty® — материал, как камни, который может пластически или хрупко деформироваться. Что контролирует, как оно будет деформироваться?
Температура: холодная глупая замазка легко ломается, но теплая глупая замазка очень пластичная.
Степень деформации: если я быстро разрываю его, он ломается, но если я медленно вытягиваю, он растягивается (пластически деформируется).
Тип стресса: Наконец, выберите сильного ученика и попросите его или ее попытаться сломать глупую замазку, используя сжимающее напряжение.Как видите, это практически невозможно. Теперь попросите ученика сломать его, используя напряжение. Это намного проще. Большинство материалов легче ломаются (или деформируются) при растяжении, чем при сжатии; мы говорим, что они слабее при растяжении или сильнее при сжатии.
Температура, скорость деформации и тип напряжения также являются ключевыми факторами деформации в ледниках. Это дает возможность вернуться к этим понятиям позже в сроке.
Относим недостатки к стрессу — подвесные стены, стенки и различные виды повреждений
Одна из целей структурной геологии состоит в том, чтобы связать природу деформации со стрессом, который вызвал ее.Поэтому важно, чтобы учащиеся могли различать нормальные неисправности (вызванные напряжением) и обратные неисправности (создаваемые сжатием).
Деревянные блоки являются ценным инструментом для обучения нормальным и обратным неисправностям. Используя три блока, срезанных под углом, можно создавать хорсты и грабены. Раздвиньте блоки, чтобы создать грабен; собрать их вместе, чтобы сделать хорст. Преимущество использования 3-х блоков состоит в том, что учащиеся могут видеть, что важна не ориентация разлома, а движение на разломе.Поскольку они могут видеть, расширяю ли я или сжимаю блоки, они интуитивно понимают разницу между нормальными и обратными ошибками. Однако учащимся, как правило, по-прежнему необходимо узнать разницу между висячей стеной и стеной для ног при сбое, чтобы точно определить, является ли сбой нормальным или обратным, и какое напряжение вызвало его.
Разломы — это места, где камни были разбиты и смещены. Нередко жидкости протекают вдоль разлома во время деформации, оставляя ценные минералы вдоль разлома.В результате многие шахты построены вдоль поверхностей разломов. Из-за этого одна сторона разлома называется висячей стеной (поверхность, с которой будет подвешен шахтерский фонарь), а одна сторона называется подножкой (поверхность, по которой будет идти шахтер).

Вот еще один способ думать об этом: подвесной настенный блок всегда находится над плоскостью разлома, в то время как ножной настенный блок всегда находится ниже плоскости разлома. Чтобы увидеть это, наведите точку на ошибку и нарисуйте вертикальную стрелку вверх.Эта стрелка указывает на висящую стену. Стрелка, указывающая прямо вниз, указывает на стену. Взгляните на слайд, который показывает ошибку и стрелки, указывающие движение. Некоторые студенты считают, что подножка выглядит как ступня. Видите, как висящая стена покоится или висит на подножке?
Когда ученики понимают разницу между висящей стеной и стеной для ног, у большинства из них возникает небольшая проблема с запоминанием того, что при обратном сбое висячая стена движется вверх, что указывает на сжатие, а при обычной ошибке висячая стена опускается, указывая на расширение.
Как ваши ученики могут видеть из этих блочных моделей, горизонтальные силы могут заставить камни двигаться вдоль разломов, которые находятся под углом к слою камней. Исходя из этой идеи, ваши учащиеся могут использовать некоторые основные тригонометрические функции для изучения взаимосвязи между горизонтальной деформацией (степень растяжения или укорачивания в горизонтальном направлении) и смещением на поверхности разлома (величина движения самого разлома). Поскольку это соотношение зависит от угла разлома от горизонтали, угол разлома является критическим компонентом того, как разломы соответствуют сокращению или расширению.
Ошибка Сиэтла — это большая обратная ошибка, которая пронизывает Сиэтл, Вашингтон, столичный регион и его почти 2 миллиона жителей. Разлом Сиэтла вмещает около 1 миллиметра сокращения в год. Однако, поскольку сама плоскость разлома плохо видна и / или не видна в сейсмических профилях, мы не знаем, какой угол этот разлом делает горизонтальным. Если неисправность является малоугловой, примерно в 25 градусах от горизонтали, то для устранения 1 мм укорачивания она должна двигаться 1.В среднем 1 мм / год Однако, если он находится на более крутых 60 градусах, он должен двигаться в среднем на 2 мм / год. Поскольку смещение разлома является основным фактором, определяющим величину землетрясения (см. Страницу о землетрясении), разлом в Сиэтле должен был бы перемещаться либо вдвое чаще, либо иметь гораздо более сильные землетрясения, если он находится под крутым углом. Косинус (A) = горизонтальная скорость укорочения / скорость смещения на разломе, где A — угол, на который разлом образует горизонталь. Решив для скорости смещения на разлом, мы получаем скорость смещения = скорость укорочения / Cos (A).Таким образом, для разлома 25 градусов, который допускает сокращение на 1 мм / год, скорость смещения будет 1 / cos (25) мм / год или 1,1 мм / год. Для ошибки в 60 градусов скорость смещения будет 1 / cos (60) мм / год или 2 мм / год.
Относящиеся аналоги к реальной Земле
Мы часто используем аналогии и аналоговые материалы (Silly Putty, песок, деревянные блоки и т. Д.), Чтобы проиллюстрировать понятия напряжения, деформации и деформации горных пород. Однако студентам иногда трудно связать эти материалы и их поведение с Землей и реальными камнями.Для этих студентов может быть полезно обсудить скорости и величины деформации на Земле и различия между камнями и аналоговыми материалами. Например, породы на границах плит часто испытывают несколько сантиметров деформации в год, но силы на них достаточны для перемещения континентов. Размер и медлительность этих процессов являются важной концепцией для общения, даже если они находятся в масштабе, который почти невозможно понять. Я иногда говорю студентам, что их ногти растут примерно с той же скоростью, что и пластины, чтобы помочь им преодолеть эту трудность.
Пластины движутся примерно с той же скоростью, что и ваши ногти, несколько сантиметров в год. Хотя это кажется медленным, в течение длительных периодов времени это действительно складывается. Например, если вы позволите вашим ногтям расти в течение 100 миллионов лет, они будут иметь длину около 4000 километров!
Примеры обучения
Суставы в кукурузном крахмале Аналог
Высушенная смесь кукурузного крахмала и воды обеспечивает интерактивное введение в суставы и наборы суставов. Учащиеся интерпретируют относительный возраст, изучают углы пересечения, используют текстуры поверхности для определения направления распространения и оценивают роль дефектов в инициации сустава.
Основы разрушения: сырный аналог
В этом задании учащиеся делают небольшие надрезы (ядра переломов) в продуктах из плавленого сыра, а затем прикладывают напряжения перпендикулярно или параллельно порезам, чтобы увидеть, как растут переломы. Удивительно (или нет, в зависимости от предыдущих мыслей о сыре), пищевые продукты из плавленого сыра ломаются почти так же, как и однородные камни.
Эволюция нормальных систем отказов во время прогрессирующей деформации
Это действие основано на фильмах QuickTime и цветных цифровых фотографиях, полученных в экспериментах с песочницей, которые дают нормальные ошибки в различных граничных условиях после экспериментов, разработанных Кеном МакКлей.Студенты просматривают специально отредактированные фильмы, чтобы узнать об эволюции нормальных систем неисправностей Затем они исследуют формирование и развитие системы разломов для конкретной структуры, отслеживая и маркируя отдельные разломы на серии фотографий, сделанных через равные промежутки времени во время эксперимента. Это упражнение помогает ученикам развить понимание возникновения, распространения, вращения и инактивации при прогрессирующей деформации.
Анализ переломов тротуара
Используя переломы на тротуарах в качестве аналога для естественных обнажений, студенты учатся систематически наблюдать, измерять ориентацию и местоположение переломов, манипулировать и анализировать данные, а также рассматривать некоторые кинематические и динамические вопросы, касающиеся происхождения и значимости переломов.
Ресурсы
Преподавание структурной геологии в 21 веке
Этот сайт содержит различные ресурсы для преподавателей, которые преподают бакалавриат структурной геологии. Вы найдете ссылки на задания и задания, интернет- и компьютерные ресурсы, полезные статьи и карты, презентации летнего семинара 2004 года по преподаванию структурной геологии, рабочие группы и дискуссионный форум, а также множество креативных идей для преподавания структурной геологии.
3D визуализация структурной деформации
GeoBlocks 3D, созданный Стивом Рейнольдсом, содержит интерактивные фильмы QuickTime Virtual Reality (QTVR), исследующие трехмерную природу геологии, в частности геологических структур внутри блоков. Вы можете вращать блоки, делать их частично прозрачными, чтобы видеть их внутреннюю структуру, прорезать или разрушать их, смещать неисправности и многое другое.
Структурная геология горных пород и регионов (вводная глава)
Этот учебник Дэвиса и Рейнольдса является наиболее широко используемым текстом структурной геологии согласно недавнему обзору.Вводная глава может быть полезной для преподавателей при размышлениях о том, как преподавать этот раздел вступительного класса, поскольку в нем рассматриваются три основных способа, которыми структурные геологи изучают деформацию: геометрический анализ, кинематический анализ и динамический анализ.
Веб-страница Стива Рейнольдса
Эта страница содержит множество инструментов визуализации и других ресурсов, разработанных и собранных Стивом Рейнольдсом, профессором геологии в Университете штата Аризона.
Курс «Структурная геология» Ресурсы в Интернете
Каталог курсов с онлайн-ресурсами или веб-страницами
,
Напряжение, деформация и модуль Юнга
Напряжение
Напряжение — это отношение приложенной силы F к площади поперечного сечения — , определяемой как « сил на единицу площади ».

растягивающее напряжение — напряжение, которое имеет тенденцию растягивать или удлинять материал — действует нормально в напряженной зоне
сжимающее напряжение — напряжение, которое имеет тенденцию сжимать или укорачивать материал — действует нормально в напряженной области
напряжение сдвига — напряжение, которое имеет тенденцию сдвигать материал — действует в плоскости напряженной области под прямым углом к напряжению сжатия или растяжения
напряжение растяжения или сжатия — нормальное напряжение
напряжение растяжения или сжатия нормальное к плоскость обычно обозначается как « нормальное напряжение » или « прямое напряжение » и может быть выражена как
σ = F _n / A (1)
, где
σ = нормальное напряжение (Па (Н / м ²), фунтов на квадратный дюйм (фунт _f / в ²))
900 04 F _n = нормальная сила, действующая перпендикулярно области (N, фунт _f)
A = площадь (м ², в ²)
a кип является имперская единица силы — она равна 1000 фунтов _ф (фунт-сила)
1 кип = 4448.2216 Ньютон (Н) = 4,4482216 кг Ньютон (кН)
Нормальная сила действует перпендикулярно области и развивается всякий раз, когда внешние нагрузки имеют тенденцию толкать или тянуть два сегмента тела.
Пример — сила растяжения, действующая на стержень
Сила 10 кН действует на круглый стержень диаметром 10 мм . Напряжение в стержне можно рассчитать как
σ = (10 10 ³ N) / (π ((10 10 ^-3 м) / 2) ²)
= 127388535 (Н / м ²)
= 127 (МПа)
Пример. Сила, действующая на столб Дугласа Пихта
Сжимающая нагрузка 30000 фунтов действует на короткий квадрат 6 x 6 дюймов пост пихты Дугласа.Одетый размер поста 5,5 x 5,5 в , а напряжение сжатия можно рассчитать как
σ = (30000 фунтов) / ((5,5 дюймов) (5,5 дюймов) ⁾
= 991 (фунт / дюйм ², фунтов на кв. дюйм)

Напряжение сдвига
Напряжение, параллельное плоскости, обычно обозначается как « напряжение сдвига » и может быть выражено как
τ = F _p / A (2)
, где
τ = напряжение сдвига (Па (Н / м ²), фунт / кв.дюйм (фунт _f / в ²))
F _p = поперечная сила в плоскости области (N, фунт _f)
A = площадь (м ², в ²)
поперечная сила лежит в плоскости площадь и развивается, когда внешние нагрузки имеют тенденцию вызывать два сегмента тело скользить друг на друга.
Напряжение (деформация)
Напряжение определяется как «деформация твердого тела из-за напряжения».
Нормальная деформация — удлинение или сжатие отрезка линии
Сдвиговая деформация — изменение угла между двумя отрезками линии, первоначально перпендикулярными
Нормальная деформация и может быть выражена как
ε = дл / л _o
= σ / E (3)
, где
dl = изменение длины (м, дюйм)
l _o = начальная длина (м, дюйм)
ε = деформация — без единиц измерения
E = модуль Юнга (модуль упругости) (Па, (Н / м ²), фунт / кв.дюйм (фунт _f / в ² ))
Модуль Юнга можно использовать для прогнозирования удлинения или сжатия объекта при воздействии силы
Обратите внимание, что деформация — это безразмерная единица, поскольку она представляет собой отношение двух длин.Но также общепринятая практика — указывать это как отношение двух единиц длины — например, м / м, или в / в .
Пример — Напряжение и изменение длины
Стержень в приведенном выше примере имеет длину 2 м и изготовлен из стали с модулем упругости 200 ГПа (200 10 ⁹ Н / м ²) . Изменение длины можно рассчитать путем преобразования (3) в
dl = σ л _o / E
= (127 10 ⁶ Па) (2 м) / (200 10 ⁹ Па)
= 0.00127 м
= 1,27 мм
Напряжение энергии
Напряжение объекта накапливает в нем энергию. Для осевой нагрузки запасенная энергия может быть выражена как
U = 1/2 F _n d
, где
U = энергия деформации (Дж (Н м), фут-фунт)
Модуль Юнга — Модуль упругости (или Модуль упругости) — Закон Гука
Большинство металлов деформируется пропорционально наложенной нагрузке в диапазоне нагрузок.Напряжение пропорционально нагрузке, а деформация пропорциональна деформации, как выражено в законе Гука .
E = напряжение / деформация
= σ / ε

= (F _n / A) / (дл / л _o) ( 4)
, где
E = модуль Юнга (Н / м ²) (фунт / дюйм ², фунт / кв. Дюйм)
Модуль упругости
, или модуль Юнга, обычно используется для металлов и металлические сплавы и выраженные в терминах 10 ⁶ фунтов _f / в ², Н / м ² или Па .Модуль упругости при растяжении часто используется для пластмасс и выражается в виде 10 ⁵ фунтов _f / в ² или ГПа .
Модуль упругости при сдвиге или модуль жесткости
G = напряжение / деформация
= τ / γ

= (F _p / A) / ( / d) (5)
, где
G = модуль упругости при сдвиге или модуль жесткости (Н / м ²) (фунт / дюйм ², фунт / кв. дюйм)
τ = напряжение сдвига ((Па) Н / м ², фунт / кв.дюйм)
γ = единица меньше меры деформации сдвига

p = сила, параллельная граням, на которые они действуют
A = площадь (м ², в ²)
s = смещение граней (м, дюйм)
d = ди Положение между смещенными гранями (м, дюйм)
Эластичность по объемному модулю
Эластичность по объемному модулю — или объемный модуль — это мера сопротивления вещества равномерному сжатию.Объемный модуль упругости — это отношение напряжения к изменению объема материала, подвергаемого осевой нагрузке.
Модули упругости
Модули упругости для некоторых распространенных материалов:
905 90 9039 9050
3,3 Основное уравнение: отношения напряжение-деформация 3.3. Основное уравнение: отношения напряжение-деформация подразделов
Учредительные уравнения говорят нам, как твердое тело деформируется (во времени) как реакция на напряжения, на изменения температуры и на поровое давление среди других. Как выбрать определяющее уравнение зависит от свойств материала, величины изменений деформации, величины напряжений и скорости нагружения среди других факторов.
Материал Модуль Юнга
— E — Модуль сдвига
— G — Модуль упругости 9 — 9000 9000 9000 900
ГПа 10 ⁶ фунтов на квадратный дюйм ГПа 10 ⁶ фунтов на кв.
Алюминий 70 10 24 3.4 70 10
Латунь 91 13 36 5,1 61 8,5
Медь 110 16 42 6,0 140 20
Стекло 55 7,8 23 3,3 37 5,2
Железо 91 90 1039 905 9038 38 38 38 38 38 5 38 90 539 38 всего 9038 905 905
Свинец 16 2.3 5,6 0,8 7,7 1,1
Сталь 200 29 84 12 160 23
Рисунок 3.9: Пример деформаций, вызванных приложенным напряжением.
$\includegraphics[scale=0.65]{.././Figures/split/4-12.pdf}$
Простейшим определяющим соотношением для твердых тел является линейная упругость, при которой напряжения и деформации линейно связаны постоянными коэффициентами. Примеры на рисунке 3.10 соответствуют приложениям линейной упругости в различных измерениях:
Рисунок 3.10: От закона Гука до обобщенной трехмерной линейной упругости.
$\includegraphics[scale=0.50]{.././Figures/split/4-13.pdf}$
Рассмотрим призматическое тело длиной , к которому мы прикладываем напряжение $\sigma_{33}$ на верхней грани 3 (рисунок 3.11). Нижняя поверхность не может двигаться в направлении 3, но может скользить вбок. Четыре других лица могут свободно двигаться во всех направлениях. Обратите внимание, что верхняя грань также может деформироваться в направлениях 1 и 2. Модуль Юнга определяется как отношение приложенного напряжения $\sigma_{33}$ и полученная деформация (в направлении приложенного напряжения) $\varepsilon_{33}$
$\displaystyle E = \frac{\sigma_{33}}{\varepsilon_{33}}$ (3.13)
Твердое тело, скорее всего, будет иметь тенденцию к увеличению в направлении, перпендикулярном приложенному напряжению. Коэффициент Пуассона (греческая буква ню) определяется как (-1) кратное отношение между деформацией, перпендикулярной приложенному напряжению. $\varepsilon_{11}$ (или $\varepsilon_{22}$ ) и деформации в направлении приложенного напряжения $\varepsilon_{33}$
$\displaystyle \nu = -\frac{\varepsilon_{11}}{\varepsilon_{33}}$ (3.14)
Эти два коэффициента являются двумя коэффициентами, обычно используемыми в качестве констант упругости в механике сплошных сред.Позже мы увидим, что в подповерхностной зоне мы почти никогда не обнаруживаем условий боковой «неограниченной» нагрузки нагрузки, как показано на рисунке 3.11.
Рисунок 3.11: Неограниченное напряженное нагружение (сжатие) линейного упругого изотропного твердого тела. Поскольку твердое тело изотропно, те же уравнения справедливы для сжатия в любом другом направлении, а также для растяжения.
$\includegraphics[scale=0.65]{.././Figures/split/4-14.pdf}$
Реальное поведение горных пород отличается от линейного упругого предположения.Рисунок 3.12 показывает схематическое представление типичного неограниченного нагрузочного теста. На рисунке показаны осевые напряжения $\sigma_a$ по вертикальной оси и осевые деформации $\varepsilon_a$ по горизонтальной оси. Часто каменные заглушки не идеально параллельны или могут иметь микротрещины. Обе особенности делают начальное поведение напряжения-деформации нагрузки менее жестким, чем фактическая жесткость породы. После начальной нагрузки порода может демонстрировать линейный отклик — где измеряется модуль Юнга — с последующим размягчением, приближающимся к разрушению породы и пиковому напряжению.Когда испытание проводится в неограниченных условиях, пиковое напряжение называется «неограниченная прочность на сжатие (UCS)» породы (более подробно объясняется в разделе 4). Коэффициент Пуассона может быть измерен в том же диапазоне измерения, что и , когда доступны датчики боковой деформации.
Рисунок 3.12: Схема напряженно-деформированной кривой при одноосном нагружении породы в лаборатории.

ПРИМЕР 3.2: Рассчитать ожидаемую (осевую) деформацию для породы, подвергнутой (аксиальному) напряжению в 3000 фунтов / кв. Дюйм при неограниченной осевой нагрузке, для:
Мягкий аргиллит с Е = 1 ГПа
Мягкий песчаник с E = 10 ГПа
Твердый известняк с E = 50 ГПа
РЕШЕНИЕ
Давайте работать в единицах СИ:
$\displaystyle \sigma_a = 3000$ МПа $\displaystyle = 3000 \frac{1}{145}$ МПа $\displaystyle = 20.7$ МПа затем $\displaystyle \varepsilon_a(1$ ГПа $\displaystyle ) = \frac{\sigma_a}{E} = \frac{20.7 \text{ MPa}}{1000 \text{ MPa}} = 0.0207 = 2.07 \%$ $\displaystyle \varepsilon_a(10$ ГПа $\displaystyle ) = \frac{\sigma_a}{E} = \frac{20.7 \text{ MPa}}{10000 \text{ MPa}} = 0.00207 = 0.207 \%$ $\displaystyle \varepsilon_a(50$ ГПа $\displaystyle ) = \frac{\sigma_a}{E} = \frac{20.7 \text{ MPa}}{50000 \text{ MPa}} = 0.00041 = 0.041 \%$
Обратите внимание, что породы могут быть довольно жесткими и даже при эффективном напряжении до 3000 фунтов на квадратный дюйм (что эквивалентно глубине на берегу 5000 футов при гидростатическом поровом давлении), деформация составляет порядка от 1% до 0.1% или меньше. $\: \: \blacksquare$
Обобщение уравнений Юнга и модуля Пуассона (уравнения 3.13 и 3.14) во всех направлениях приводит к трем независимым уравнениям.
$\begin{displaymath}\left\lbrace \begin{array}{rcl} \varepsilon_{11} & = & +\cfra... ...\: \sigma_{22} + \cfrac{1}{E} \: \sigma_{33} \end{array}\right.\end{displaymath}$ (3.15)
Кроме того, сдвиговые деформации $\varepsilon_{ij}$ пропорциональны приложенному напряжению сдвига через модуль сдвига $G=E/[2(1+\nu)]$ , такой, что
,
Share This Post :