Напряжение и деформация — 2018
Внутренние силы в том или ином теле меняются от одной точки к другой. По всякой малой внутренней плоской области нагрузки вызываются частью тела на одной стороне такой области в отношении части на другой стороне. Напряжение обозначает интенсивность этих термических сил (сила на единичную площадку).
Напряжение
В непрерывном теле напряжение в точке можно вычислить следующим образом:- Представьте произвольную плоскость, пересекающую тело в такой точке.
- Рассмотрите бесконечно малую площадь ΔA вокруг этой точки на плоскости.
- Предположим, что величина силы, передаваемой через ΔA в определенном направлении, равна ΔF.
- Тогда напряжение в этом направлении равно ΔF/ΔA по мере приближения ΔA к 0.
Выше приведено определение напряжения или вектора тягового усилия в точке. Состояния напряжение в точке определяется не только вектором тягового усилия. Изменения также зависят от выбранной произвольной плоскости.
Рисунок (1): Плоскость, проходящая через точку O и разделяющая тело на две части.
Рисунок (2): Векторы результирующей силы и момента в районе области ΔA около точки O в плоскости.
Рисунок (3): Вектор ограничивающего сжатия в точке O на плоскости.
Напряжение
Деформация представляет собой отношение изменения длины δL к исходной длине L. Деформация является безразмерной величиной.
Деформация = δL/L
Последовательность вычислений
Если задана модель с сеткой и набором ограничений перемещения и нагрузок, то программа линейного статического анализа поступает следующим образом.- Программа составляет и решает систему линейных совместных уравнений равновесия конечных элементов для вычисления составляющих перемещения в каждом узле.

- Далее использует результаты по перемещениям для расчета составляющих деформации.
- Программа использует результаты расчета деформации и отношение напряжение-деформация для вычисления напряжений.
Расчеты напряжений
Результаты расчета напряжений сначала вычисляются в специальных точках, называемых гауссовыми точками или точками квадратуры, расположенными внутри каждого элемента. Эти точки выбираются таким образом. чтобы получить оптимальные числовые результаты. Программа вычисляет напряжения в узлах каждого элемента при помощи экстраполирования результатов, доступных в гауссовых точках.
 Если, например, некий узел являются общим для трех элементов, могут быть получены три слегка отличающихся значения для каждого компонента в такой точке.
Если, например, некий узел являются общим для трех элементов, могут быть получены три слегка отличающихся значения для каждого компонента в такой точке.
При просмотре результатов по напряжениям, вам могут понадобиться элементные напряжения или узловые напряжения. Для вычисления элементных напряжений программа усредняет соответствующие узловые напряжения для каждого элемента. Для расчета узловых напряжений программа усредняет соответствующий результат по всем элементам, делящим между собой такую узловую точку.
Открытая Физика. Деформация
В твердых телах – аморфных и кристаллических – частицы (молекулы, атомы, ионы) совершают тепловые колебания около положений равновесия, в которых энергия их взаимодействия минимальна. При увеличении расстояния между частицами возникают силы притяжения, а при уменьшении – силы отталкивания (см. §3.1). Силы взаимодействия между частицами обусловливают механические свойства твердых тел.Деформация твердого тела является результатом изменения под действием внешних сил взаимного расположения частиц, из которых состоит тело, и расстояний между ними.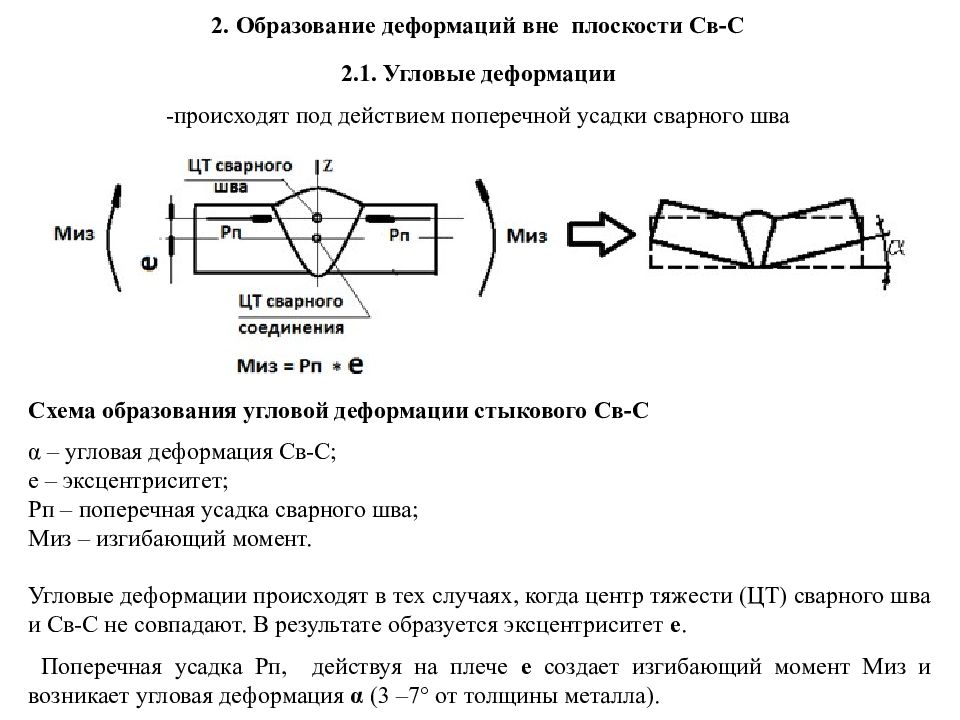
Существует несколько видов деформаций твердых тел. Некоторые из них представлены на рис. 3.7.1.
Простейшим видом деформации является деформация растяжения или сжатия. Ее можно характеризовать абсолютным удлинением
Отношение абсолютного удлинения Δl к первоначальной длине l образца называется относительным удлинением или относительной деформацией ε: ε=Δll.
При растяжении ε > 0, при сжатии ε < 0.
Если принять направление внешней силы, стремящейся удлинить образец, за положительное, то F > 0 при деформации растяжения и F < 0 – при сжатии. Отношение модуля внешней силы F к площади S сечения тела называется механическим напряжением σ:
σ=FS.
Отношение модуля внешней силы F к площади S сечения тела называется механическим напряжением σ:
σ=FS.
За единицу механического напряжения в СИ принят паскаль (Па). Механическое напряжение измеряется в единицах давления.
Зависимость между ε и σ является одной из важнейших характеристик механических свойств твердых тел. Графическое изображение этой зависимости называется диаграммой растяжения. По оси абсцисс откладывается относительное удлинение ε, а по оси ординат – механическое напряжение σ. Типичный пример диаграммы растяжения для металлов (таких как медь или мягкое железо) представлен на рис. 3.7.2.
При малых деформациях (обычно существенно меньших 1 %) связь между σ и ε оказывается линейной (участок Oa на диаграмме). При этом при снятии напряжения деформация исчезает.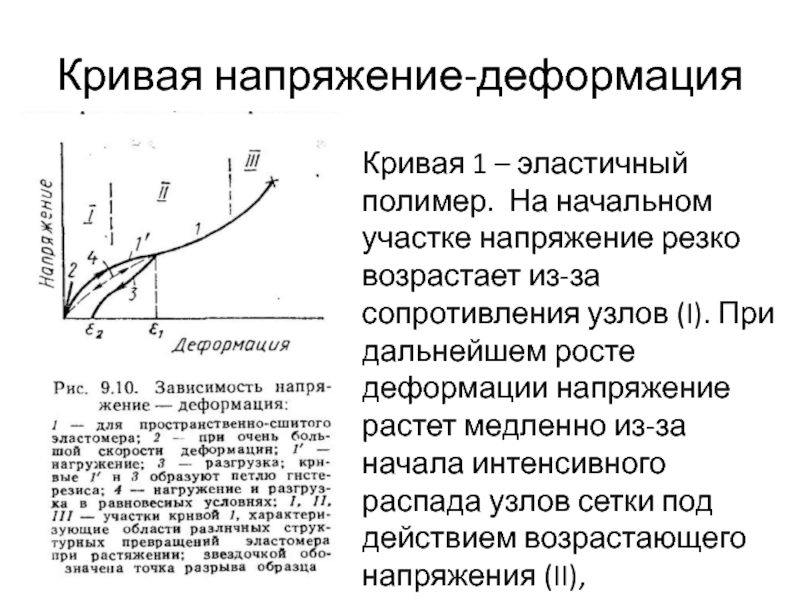 Такая деформация называется упругой. Максимальное значение
Такая деформация называется упругой. Максимальное значение
Коэффициент E в этом соотношении называется модулем Юнга.
При дальнейшем увеличении напряжения связь между σ и ε становится нелинейной (участок ab). Однако при снятии напряжения деформация практически полностью исчезает, т. е. восстанавливаются размеры тела. Максимальное напряжение на этом участке называется пределом упругости .
Если σ > σупр, образец после снятия напряжения уже не восстанавливает свои первоначальные размеры и у тела сохраняется остаточная деформация εост. Такие деформации называются пластическими (участки bc, cd и de). На участке bc деформация происходит почти без увеличения напряжения.
Материалы, у которых диаграмма растяжения имеет вид, показанный на рис. 3.7.2, называются пластичными. У таких материалов обычно деформация εmax, при которой происходит разрушение, в десятки раз превосходит ширину области упругих деформаций. К таким материалам относятся многие металлы.
Материалы, у которых разрушение происходит при деформациях, лишь незначительно превышающих область упругих деформаций, называются хрупкими (стекло, фарфор, чугун).
Аналогичным закономерностям подчиняется и деформация сдвига (рис. 3.7.1 (2)). В этом случае вектор силы F→ направлен по касательной к поверхности образца. Относительная деформация определяется безразмерным отношением
 При малых деформациях
Δxl=1GFS.
При малых деформациях
Δxl=1GFS.Коэффициент пропорциональности G в этом отношении называется модулем сдвига. Модуль сдвига для большинства твердых материалов в 2–3 раза меньше модуля Юнга. Например, у меди E = 1,1·1011 Н/м2, G = 0,42·1011 Н/м2. Следует помнить, что у жидких и газообразных веществ модуль сдвига равен нулю.
На рис. 3.7.1 (3) показана деформация всестороннего сжатия твердого тела, погруженного в жидкость. В этом случае механическое напряжение совпадает с давлением p в жидкости. Относительная деформация определяется как отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях ΔVV=1Bp.
Коэффициент пропорциональности B в этой формуле называется модулем всестороннего сжатия.
Всестороннему сжатию могут подвергаться не только твердые тела, но и жидкости и газы. У воды B = 2,2·109 Н/м2, у стали B = 1,6·1011 Н/м2. На дне Тихого океана, на глубине порядка 4 км, давление p приблизительно равно 4·107 Н/м2. В этих условиях относительное изменение ΔV / V объема воды составляет 1,8 %, в то время как для стального тела оно составляет всего лишь 0,025 %, т. е. в 70 раз меньше. Твердые тела с их жесткой кристаллической решеткой значительно менее сжимаемы по сравнению с жидкостями, атомы и молекулы которых не так сильно связаны со своими соседями. Сжимаемость газов на много порядков выше, чем у жидкостей и твердых тел.
На дне Тихого океана, на глубине порядка 4 км, давление p приблизительно равно 4·107 Н/м2. В этих условиях относительное изменение ΔV / V объема воды составляет 1,8 %, в то время как для стального тела оно составляет всего лишь 0,025 %, т. е. в 70 раз меньше. Твердые тела с их жесткой кристаллической решеткой значительно менее сжимаемы по сравнению с жидкостями, атомы и молекулы которых не так сильно связаны со своими соседями. Сжимаемость газов на много порядков выше, чем у жидкостей и твердых тел.
Величина модуля всестороннего сжатия определяет скорость звука в данном веществе (см. §2.7).
Напряжения и деформации при растяжении и сжатии. расчет на прочность и жесткость
Содержание:
Напряжения и деформации при растяжении и сжатии. расчет на прочность и жесткость
- Напряжение и деформация Под напряжением и сжатием. Расчет прочности и жесткости Натяжение или сжатие стержня вызвано силами, действующими вдоль основания.
 При этом в поперечном сечении стержней из шести коэффициентов внутренней силы имеется только один-продольная (осевая) сила N. простейший случай растяжения стержня и график продольной силы показаны
При этом в поперечном сечении стержней из шести коэффициентов внутренней силы имеется только один-продольная (осевая) сила N. простейший случай растяжения стержня и график продольной силы показаны
на рисунке. 95, a, b. осевая сила в поперечном сечении является результатом вертикального напряжения, возникающего в каждой из точек поперечного сечения. Отсутствие боковых сил говорит о том, что напряжение сдвига в каждой точке поперечного сечения равно нулю. Получены уравнения для определения нормального напряжения. Чтобы решить эту проблему, следуйте порядку, указанному в§ 26. Дополнительное поперечное сечение p-p
(рис. 95, в). Статический аспект задачи представлен уже известной формулой Людмила Фирмаль
(3.29): N = JodF. (4.1)) Ф Из уравнения (4.1) невозможно определить величину КТ, так как закон распределения последнего в точке поперечного сечения неизвестен. Рассмотрим геометрический аспект задачи. Наблюдение деформации расширения и сжатия бруска на поверхности, на которой размещена линия, перпендикулярная оси бруска(рис. 95, а), может быть б Следует отметить, что эти линии движутся параллельно самим себе и остаются прямыми
95, а), может быть б Следует отметить, что эти линии движутся параллельно самим себе и остаются прямыми
и перпендикулярными оси луча. Предполагая, что картина смещения этого участка происходит внутри стержня, предположим, что поперечное сечение стержня является плоским до деформации, и разделим поступательно движущиеся стержни вдоль оси стержня на продольные (параллельные оси стержня) элементы бесконечно малого сечения и назовем их в дальнейшем волокнами. Исходя
- из гипотезы плоского поперечного сечения, следует сделать вывод, что все волокна удлиняются на одну и ту же величину, а их удлинение е одинаково: е= — г — = const и. (4.2) это аналитическое представление геометрического аспекта задачи. Физический аспект задачи заключается в установлении зависимости напряжения от деформации. При упругой деформации эта зависимость линейна и, как известно, называется законом крюка: e=, или / <t= = E|, (4.3) где E-модуль упругости, модуль упругости первого рода или коэффициент пропорциональности, называемый модулем Юнга.
 Модуль упругости является одной из физических констант материала. Модуль упругости измеряется в единицах напряжения. 86 инвариантность модуля
Модуль упругости является одной из физических констант материала. Модуль упругости измеряется в единицах напряжения. 86 инвариантность модуля
упругости е однородных изотропных материалов, а также Формулы (4.2) и (4.3) показывают следующее А ее-то=const. (4.4) подставляя формулу (4.4) в Формулу (4.1), можно увидеть, что (V=J EedF=her J dF=EeF=oF, (4.5) G Ф Откуда (4-6)) Знак напряжения зависит от знака продольной силы рассматриваемого сечения. В случае сжатия, напряжение считается отрицательным. Следует отметить, что формула (4.6) справедлива только для участков, находящихся на значительном удалении от места приложения сосредоточенной нагрузки. Вблизи приложения нагрузки распределение напряжений является сложным и требует более точного метода
исследования. Если система сил совпадает с ее основным вектором и основным Людмила Фирмаль
моментом, то есть размерами области приложения нагрузки, то сечение сравнивается с размерами тела. Общетеоретического доказательства принципа Сен-Венана нет, но его обоснованность подтверждается многими теоретическими и экспериментальными исследованиями. Этот принцип объясняется в следующем примере. Тот же стержень закреплен верхним концом(рис. 96) нагрузка на свободный конец со статической эквивалентной нагрузкой, а результат представлен величиной вектора R, прикладывается различными способами: а-в виде сосредоточенной осевой силы; б—в
Общетеоретического доказательства принципа Сен-Венана нет, но его обоснованность подтверждается многими теоретическими и экспериментальными исследованиями. Этот принцип объясняется в следующем примере. Тот же стержень закреплен верхним концом(рис. 96) нагрузка на свободный конец со статической эквивалентной нагрузкой, а результат представлен величиной вектора R, прикладывается различными способами: а-в виде сосредоточенной осевой силы; б—в
виде двух сил; согласно исследованию, во всех случаях в поперечном сечении снимается на расстояние, превышающее 1,5-2 его поперечных сечения, в сечениях, расположенных в середине сечения, величина напряжения и характер его распределения различны. 87перейдем к определению деформации стержня. Из Формулы (4.5) можно найти относительное удлинение: Л е В пределах призматической части длины стержня/, выполненного
из однородного материала (£=const) одинаковой продольной силы/V, сечение удлинения каждого узла- Рис девяносто семь Вязать по длине одинаково, а значит и абсолютное удлинение Ми=/ N1 L’c•(4. 8) — ч Л р р Но +«„Х J Т — — — — — — — -“ Дж — Г Один. т а г Но б Рис девяносто восемь Формула (4.8)представляет закон крюка для абсолютного расширения. Знаменатель формулы для произведения ££_ называется жесткостью. Величина=называется жесткостью поперечного сечения стержня. Под напряжением и сжатием существует и диапазон сил. Она принадлежит роду. Т(Рис. 97, А-Е), то для элементов тонкой длины
8) — ч Л р р Но +«„Х J Т — — — — — — — -“ Дж — Г Один. т а г Но б Рис девяносто восемь Формула (4.8)представляет закон крюка для абсолютного расширения. Знаменатель формулы для произведения ££_ называется жесткостью. Величина=называется жесткостью поперечного сечения стержня. Под напряжением и сжатием существует и диапазон сил. Она принадлежит роду. Т(Рис. 97, А-Е), то для элементов тонкой длины
dx(рис. 97, g) можно записать на основе формулы (4.8 д (ДХ)= Е Ф(Х }. Полное расширение участка по длине получается полным расширением всех бесконечно малых участков: (4.9) Смещение одного участка относительно другого равно продольной деформации участка стержня, замкнутого между рассматриваемыми участками и вытягивающего книгу (7) 98). Он уменьшается при растяжении и увеличивается при сжатии. По аналогии с продольным вариантом разность соответствующих поперечных размеров после и до него
называется АВ- 88салютной поперечной деформации: & (4.10)) Да= — а; Ди-БТ-б. При растяжении поперечная деформация отрицательна, а при сжатии-положительна. (4.При сжатии напряжение в формуле необходимо заменить на 14) (4.14) Бо знаком „минус“.» Коэффициент Пуассона p и модуль упругости E характеризуют упругие свойства
(4.При сжатии напряжение в формуле необходимо заменить на 14) (4.14) Бо знаком „минус“.» Коэффициент Пуассона p и модуль упругости E характеризуют упругие свойства
материала. Для всех изотропных материалов значение коэффициента Пуассона находится в диапазоне от 0 до 0. 5. В частности, пробка Р близка к нулю, резина к 0,5, сталь Р ближе к 0,3. Значения модуля Е и коэффициента р для некоторых материалов приведены в приложении 9.
Смотрите также:
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings. TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings. AUTHOR}}
AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}%d0%ba%d1%80%d0%b8%d0%b2%d0%b0%d1%8f%20%d0%bd%d0%b0%d0%bf%d1%80%d1%8f%d0%b6%d0%b5%d0%bd%d0%b8%d0%b5%20%e2%80%93%20%d0%b4%d0%b5%d1%84%d0%be%d1%80%d0%bc%d0%b0%d1%86%d0%b8%d1%8f — со всех языков на все языки
Все языкиРусскийАнглийскийИспанский────────Айнский языкАканАлбанскийАлтайскийАрабскийАрагонскийАрмянскийАрумынскийАстурийскийАфрикаансБагобоБаскскийБашкирскийБелорусскийБолгарскийБурятскийВаллийскийВарайскийВенгерскийВепсскийВерхнелужицкийВьетнамскийГаитянскийГреческийГрузинскийГуараниГэльскийДатскийДолганскийДревнерусский языкИвритИдишИнгушскийИндонезийскийИнупиакИрландскийИсландскийИтальянскийЙорубаКазахскийКарачаевскийКаталанскийКвеньяКечуаКиргизскийКитайскийКлингонскийКомиКомиКорейскийКриКрымскотатарскийКумыкскийКурдскийКхмерскийЛатинскийЛатышскийЛингалаЛитовскийЛюксембургскийМайяМакедонскийМалайскийМаньчжурскийМаориМарийскийМикенскийМокшанскийМонгольскийНауатльНемецкийНидерландскийНогайскийНорвежскийОрокскийОсетинскийОсманскийПалиПапьяментоПенджабскийПерсидскийПольскийПортугальскийРумынский, МолдавскийСанскритСеверносаамскийСербскийСефардскийСилезскийСловацкийСловенскийСуахилиТагальскийТаджикскийТайскийТатарскийТвиТибетскийТофаларскийТувинскийТурецкийТуркменскийУдмуртскийУзбекскийУйгурскийУкраинскийУрдуУрумскийФарерскийФинскийФранцузскийХиндиХорватскийЦерковнославянский (Старославянский)ЧеркесскийЧерокиЧеченскийЧешскийЧувашскийШайенскогоШведскийШорскийШумерскийЭвенкийскийЭльзасскийЭрзянскийЭсперантоЭстонскийЮпийскийЯкутскийЯпонский
Все языкиРусскийАнглийскийИспанский────────АймараАйнский языкАлбанскийАлтайскийАрабскийАрмянскийАфрикаансБаскскийБашкирскийБелорусскийБолгарскийВенгерскийВепсскийВодскийВьетнамскийГаитянскийГалисийскийГреческийГрузинскийДатскийДревнерусский языкИвритИдишИжорскийИнгушскийИндонезийскийИрландскийИсландскийИтальянскийЙорубаКазахскийКарачаевскийКаталанскийКвеньяКечуаКитайскийКлингонскийКорейскийКрымскотатарскийКумыкскийКурдскийКхмерскийЛатинскийЛатышскийЛингалаЛитовскийЛожбанМайяМакедонскийМалайскийМальтийскийМаориМарийскийМокшанскийМонгольскийНемецкийНидерландскийНорвежскийОсетинскийПалиПапьяментоПенджабскийПерсидскийПольскийПортугальскийПуштуРумынский, МолдавскийСербскийСловацкийСловенскийСуахилиТагальскийТаджикскийТайскийТамильскийТатарскийТурецкийТуркменскийУдмуртскийУзбекскийУйгурскийУкраинскийУрдуУрумскийФарерскийФинскийФранцузскийХиндиХорватскийЦерковнославянский (Старославянский)ЧаморроЧерокиЧеченскийЧешскийЧувашскийШведскийШорскийЭвенкийскийЭльзасскийЭрзянскийЭсперантоЭстонскийЯкутскийЯпонский
Сварочные напряжения и деформация, способы уменьшения деформации
Такие моменты неизбежны при сварке. Практически каждый специалист не раз наблюдал в процессе соединения элементов, как возникают сварочные напряжения и деформация. Эти явления отнюдь не безобидны. Их возникновение негативно сказывается на качестве шва и снижает прочность всех соединений.
Практически каждый специалист не раз наблюдал в процессе соединения элементов, как возникают сварочные напряжения и деформация. Эти явления отнюдь не безобидны. Их возникновение негативно сказывается на качестве шва и снижает прочность всех соединений.
Почему возникают такие явления?
Существует множество факторов, вызывающих напряжения и деформацию во время сварки. Основными их них являются три:
- Перемены в структуре соединения.
Такие явления оказывают и растягивающие, и сжимающие воздействия на боковые области стали, как увеличивая, так и уменьшая его объем. При значительном содержании углерода в составе материала изменения довольно большие. Иногда они становятся причиной трещинок на поверхности детали.
- Литейная усадка стали.
Это явление образуется в сварном шве тогда, когда материал остывает и уменьшается. В области, которая была нагрета, появляются силы, тянущие за собой близкие участки. Поэтому в стали возникает напряжение и деформация.
 Чем больше металла было разогрето, тем наибольшие изменения происходят.
Чем больше металла было разогрето, тем наибольшие изменения происходят. - Прогрев или охлаждение стали в неодинаковом объеме.
Когда вы нагреваете металлическое изделие, оно расширяется. Если при этом вы производите сварной шов, то увеличение объема идет неравномерно. Прогреваемая область влияет на материал ближней зоны, который пока холодный. Результатом становится деформация. На ее степень влияет способность металла проводить тепло, чем она меньше, тем больше разрушительные изменения. Кроме того, влияет и температура, до которой сталь нагревается в процессе сварки.
Как уменьшить сварочное напряжение и деформации?
Такие факторы негативно влияют на прочностные характеристики деталей, вплоть до разрушения всей свариваемой конструкции. Профессионалы имеют множество способов устранения этих явлений.
Чтобы сварочное напряжение и деформация были минимальными, следует делать следующее:
- Тщательно выбирать конструкцию сварной детали.

- Верно подбирать место соединения.
- Правильно определять последовательности выполнения сварных соединений (в случаях, когда их планируется сделать несколько). Также следует помнить о том, что она должна допускать не затрудненную ничем деформацию всей детали.
- Подбирать верный режим сварки. Например, длинные швы делают обратноступенчатым методом. Сварка нескольких слоев нуждается в каскадном способе.
Изучите кривую деформации при растяжении в одной статье
Свойства материала с точки зрения деформации и повреждения под действием растягивающих усилий можно измерить по кривой растяжения, которая является одной из самых фундаментальных и важных концепций в механике материалов, и я пришел со мной, чтобы понять ее.
Горизонтальная координата кривой — это деформация, а вертикальная координата — это напряжение. Форма кривой отражает различные деформационные процессы, происходящие в материале под действием внешних сил.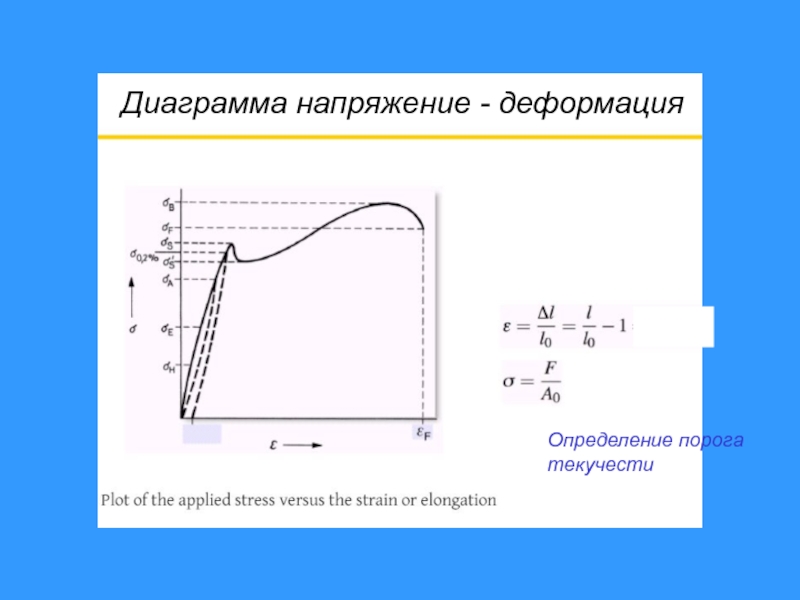
Все мы знаем, что тремя элементами силы являются величина, направление и точка действия. Однако точка действия не имеет размеров, она просто отображает расположение силы. Материал объекта имеет размеры, и когда нам нужно изучить силы в различных точках внутри объекта, нам нужно ввести понятие напряжения, выраженное как σ.
Формула растягивающего напряжения: σ = dF / dA, которое представляет напряжение на единицу площади внутри материала. С точки зрения непрофессионала, растягивающее напряжение — это сопротивление на единицу площади внутри объекта, когда объект подвергается внешнему воздействию, с чувством общей защиты от внешних врагов.
Как показано выше, объект подвергается растягивающей силе, затем, чтобы уравновесить эту силу, материал на единицу площади внутри объекта подвергается части силы.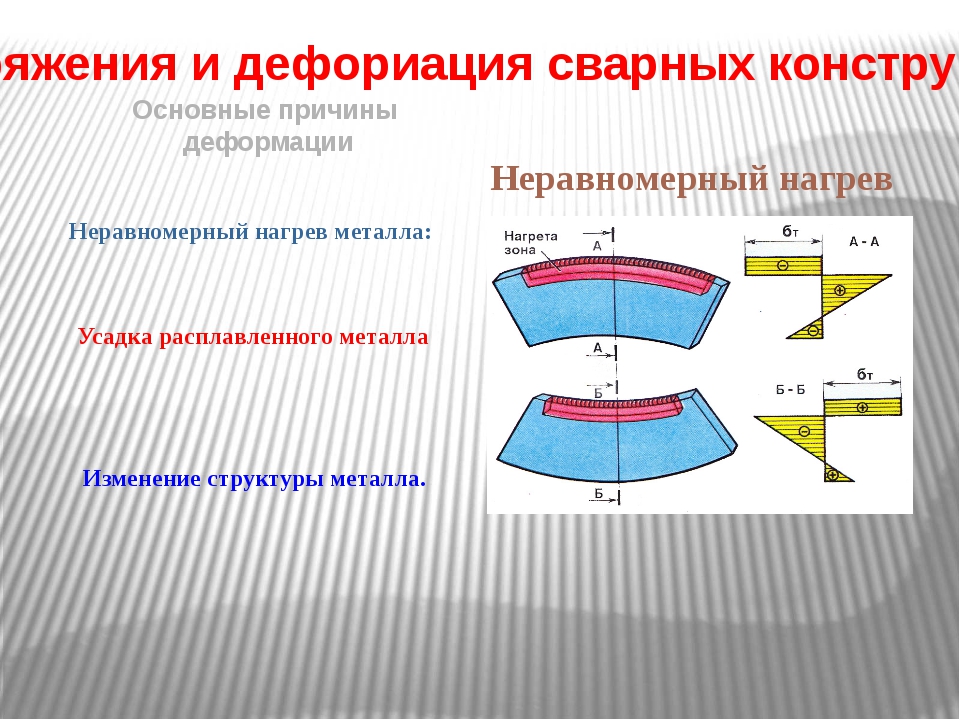 Когда плоскость внутри объекта перпендикулярна направлению силы, а материал однороден, применяется среднее растягивающее напряжение. Под действием этого растягивающего напряжения деформация, отражающая объект, называется деформацией.
Когда плоскость внутри объекта перпендикулярна направлению силы, а материал однороден, применяется среднее растягивающее напряжение. Под действием этого растягивающего напряжения деформация, отражающая объект, называется деформацией.
Как показано на диаграмме ниже: кривая напряжения-деформации обычно делится на четыре стадии: упругая область, область течения, деформационное упрочнение и трещина с образованием шейки.
1 эластичный областьХарактеристики: Когда напряжение ниже σe, напряжение пропорционально деформации образца, напряжение снимается и деформация исчезает, т.е. образец находится в фазе упругой деформации. После того, как нагрузка превышает значение, соответствующее точке «а», кривая растяжения начинает отклоняться от прямой линии.
Важное понятие: σe — предел упругости материала и представляет собой максимальное напряжение, при котором материал остается упруго деформированным. В упругой фазе есть специальный линейный сегмент «оа», в котором существует линейная зависимость между σ и ε. Это называется пропорциональной фазой, также известной как линейная упругая фаза. Удовлетворение закону Гука.
В упругой фазе есть специальный линейный сегмент «оа», в котором существует линейная зависимость между σ и ε. Это называется пропорциональной фазой, также известной как линейная упругая фаза. Удовлетворение закону Гука.
σ = E * ε
E называется модулем упругости материала, обычно для стали E = 200 ГПа.
Пропорциональный предел σp — это максимальное значение напряжения, которое подчиняется закону Гука между напряжением и деформацией.
Ноты:
σ и ε подчиняются закону Гука только тогда, когда напряжение F / A <σp.
При σp <σ <σe закон Гука больше не выполняется в сечении ab, но это все еще упругая деформация.
Поскольку разница между σp и σe незначительна, в инженерии различий не делается.
Характеристики: Когда напряжение превышает σe до определенного значения, линейная зависимость между напряжением и деформацией нарушается, и деформация значительно увеличивается, в то время как напряжение сначала уменьшается, а затем колеблется в мгновение ока, при этом небольшие сегменты пилообразной линии появляются рядом с горизонтальной линией на кривой.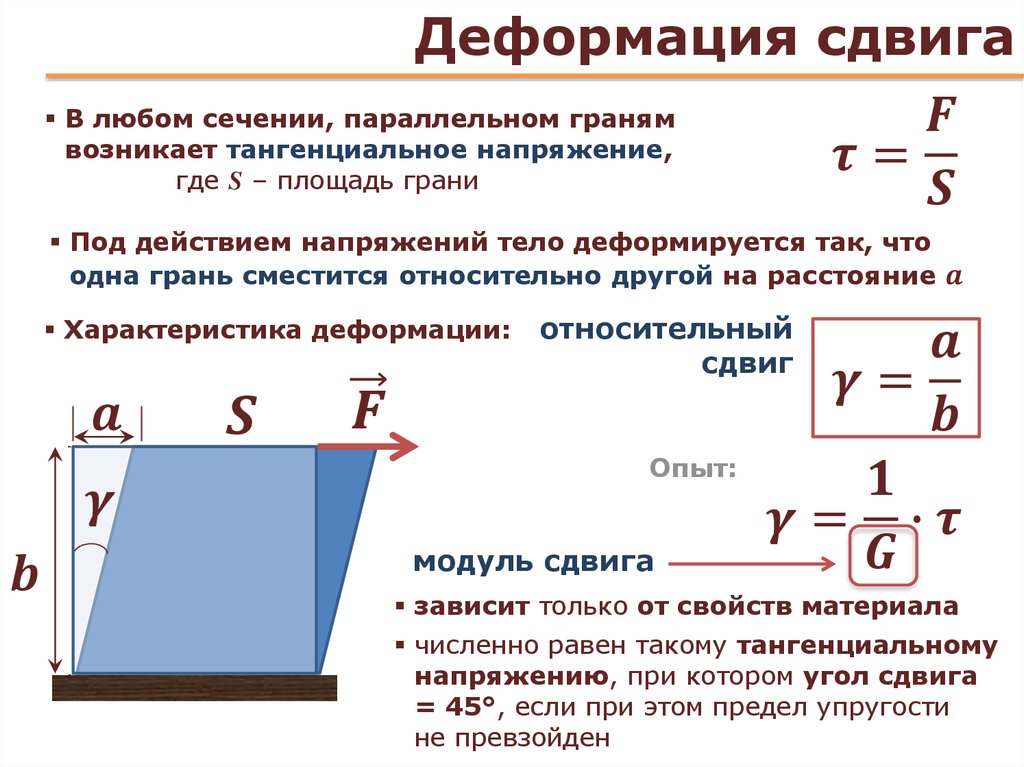 В ненагруженном состоянии деформация образца восстанавливается только частично, сохраняя при этом часть остаточной деформации, то есть пластической деформации. Это свидетельствует о переходе деформации материала в фазу упругопластической деформации.
В ненагруженном состоянии деформация образца восстанавливается только частично, сохраняя при этом часть остаточной деформации, то есть пластической деформации. Это свидетельствует о переходе деформации материала в фазу упругопластической деформации.
Важное понятие: σs называется пределом текучести или пределом текучести материала и является важным показателем пластичности. Для материалов без значительной текучести в инженерии значение напряжения, которое вызывает остаточную деформацию 0.2%, определяется как предел текучести.
При испытании на растяжение, если образец податился, то есть сечение «bc» на диаграмме выше, образец продолжает удлиняться, даже если нагрузка больше не увеличивается, и, таким образом, на кривой растяжения появляется горизонтальный интервал, явление, известное как текучесть или текучесть. Явление текучести вызвано проскальзыванием кристаллов в металле. Для материалов без пластической деформации в технических нормах указано, что напряжение, соответствующее 0. 2% пластической деформации, используется в качестве предела текучести, записанного как σ0.2.
2% пластической деформации, используется в качестве предела текучести, записанного как σ0.2.
Характеристики: Когда напряжение превышает σs, образец подвергается значительной и равномерной пластической деформации, если напряжение на образце увеличивается, значение напряжения должно быть увеличено. Это явление увеличения сопротивления пластической деформации по мере увеличения пластической деформации известно как наклеп или деформационное упрочнение.
Важное понятие: Фаза равномерного деформирования образца заканчивается, когда напряжение достигает σb. Это максимальное напряжение σb называется пределом прочности или пределом прочности материала на растяжение, что указывает на сопротивление материала максимальной однородной пластической деформации, то есть максимальное напряжение, которое материал может выдержать до разрушения при растяжении.
4 Перелом шейки
Характеристики: После достижения значения напряжения σb образец начинает неравномерно деформироваться и образовывать усадочную шейку, напряжение падает, и, наконец, образец разрушается, когда напряжение достигает σf.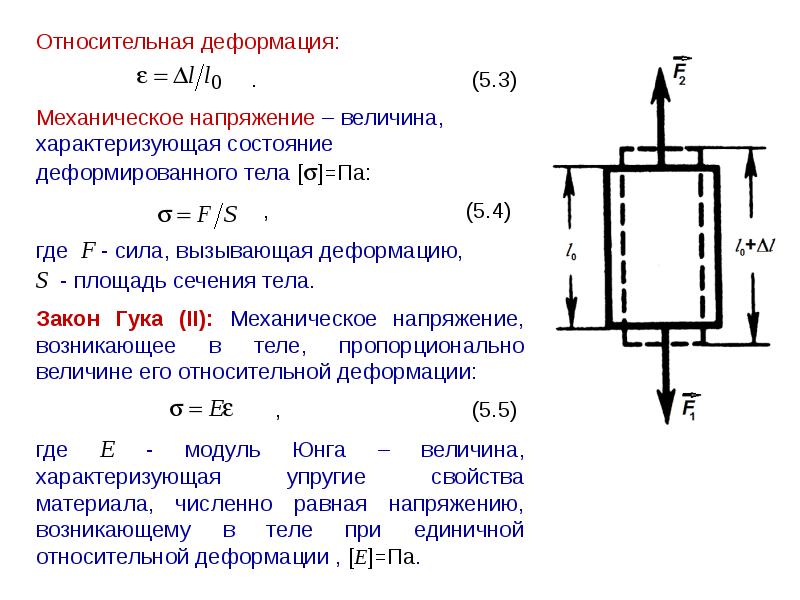
Важное понятие: σf — это предел прочности материала на излом, который представляет собой предельное сопротивление материала пластичности. В целом показателями пластических свойств материала являются удлинение и уменьшение площади.
Относительное удлинение: δ = (L1-L) / L * 100%
Уменьшение площади: ψ = (A-A1) / A * 100%
L1: длина образца после снятия
L: исходная длина образца
A1: минимальная площадь поперечного сечения образца на изломе
A: исходная площадь поперечного сечения
Чем больше значение δ и ψ, тем лучше пластичность.
В технике материалы с удлинением ≥5% после разрыва обычно называют пластическими материалами, а материалы с удлинением <5% после разрыва называют хрупкими материалами. Как правило, можно видеть, что пластмассовые материалы имеют отчетливую фазу текучести, в то время как разрушение при растяжении образует шейку. Напротив, хрупкие материалы не видят явной фазы текучести во время растяжения, и при растяжении трещин не происходит образования шейки.
Напротив, хрупкие материалы не видят явной фазы текучести во время растяжения, и при растяжении трещин не происходит образования шейки.
Пластиковый материал: очень маленькая эластичная область.
Пластичный материал: после упругой области есть странный участок, на котором происходит «сужение» — в этой пластической области происходит постоянная деформация.
Прочный, не пластичный материал: стальная проволока очень мало растягивается и внезапно ломается.
Хрупкий материал: этот материал также прочен, потому что при высоких напряжениях мало деформации. Разрушение хрупкого материала происходит внезапно с небольшой пластической деформацией или без нее. Стекло — это хрупкое напряжение.
Сравнение механических свойств пластичных и хрупких материалов.
| Пластмасса | Хрупкий материал |
| Относительное удлинение: δ≥5% | Относительное удлинение: δ 5% |
| Большая пластическая деформация перед разрушением | Очень небольшая деформация перед разрушением |
| Характеристики сжатия и растяжения аналогичны | Производительность на сжатие намного выше, чем на растяжение |
| Подходит для ковки и холодной обработки | Подходит для элементов фундамента или оболочки |
Примечание: пластичность и хрупкость материала могут быть изменены в результате изменения методов производства и условий процесса.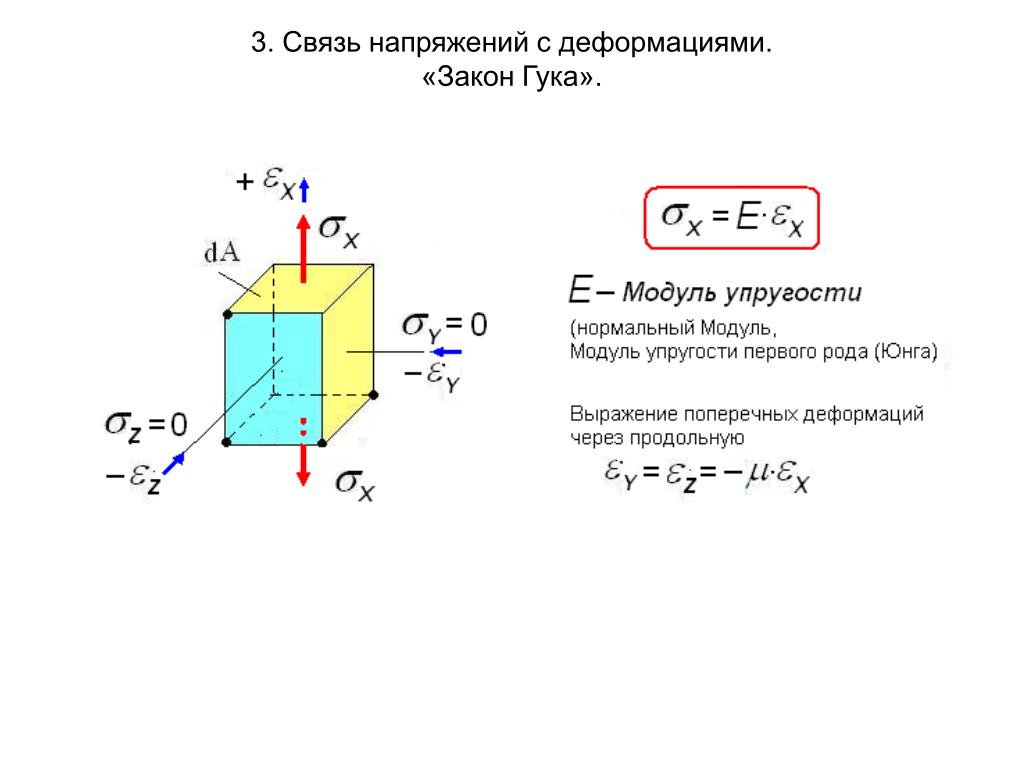 | |
Вот и все, что касается кривой растяжения-напряжения, если вы хотите знать, как выполнять испытание на разрыв, смотрите здесь.
Напряжение, деформация и модуль Юнга
Напряжение
Напряжение представляет собой отношение приложенной силы F к площади поперечного сечения — , определяемой как « силы на единицу площади ».
- растягивающее напряжение — напряжение, стремящееся к растяжению или удлинению материала, — действует нормально к напряженной области
- сжимающее напряжение — напряжение, стремящееся сжать или укоротить материал — действует нормально к напряженной области
- напряжение сдвига — напряжение, стремящееся к сдвигу материала — действует в плоскости к напряженной зоне под прямым углом к напряжению сжатия или растяжения
Напряжение растяжения или сжатия — нормальное напряжение
Напряжение растяжения или сжатия, нормальное к плоскости Обычно обозначается « нормальный стресс » или « прямой стресс » и может быть выражен как
σ = F N / A (1)
, где
Σ = нормальное напряжение (Па (Н/м 2 ), фунтов на квадратный дюйм ( фунт f / дюйм 2 ))
F N = нормальная сила, действующая перпендикулярность площади (N, LB F )
A = площадь (M 2 , в 2 )
- A KIP — имперский единица силы — равна 1000 фунтов f (фунт-сила)
- 1 кип = 4448.
 2216 ньютонов (Н) = 4,4482216 килоньютонов (кН)
2216 ньютонов (Н) = 4,4482216 килоньютонов (кН)
Нормальная сила действует перпендикулярно площади и развивается всякий раз, когда внешние нагрузки стремятся толкать или тянуть два сегмента тела.
Пример. Сила растяжения, действующая на стержень
Сила 10 кН действует на круглый стержень диаметром 10 мм . Стресс в стержне можно рассчитать как
Σ = (10 10 3 N) / (π ((10 10 -3 м) / 2) 2 )
= 127388535 (Н/м 2 )
= 127 (МПа)
Пример. Сила, действующая на квадратную стойку из пихты Дугласа
столб пихты Дугласа.Размер штифта в зачищенном виде составляет 5,5 x 5,5 дюйма , а сжимающее напряжение можно рассчитать как
σ = (30000 фунтов) / ((5,5 дюйма) (5,5 дюйма) )
1 9000 = 7 (LB / IN 2 , PSI)Стресс сдвига
Стресс, параллельный на плоскости, обычно обозначается как «
стресса сдвига » и может быть выражена какτ = F P / A (2)
, где , где 1
τ = напряжение сдвига (PA (N / M 2 ), PSI (LB F / в 2 ))
F p = поперечная сила в плоскости площади (Н, фунт f )
A = площадь (м 2 , in 2 )
A лежит в плоскости поперечной силы области и развивается, когда внешние нагрузки имеют тенденцию вызывать два сегмента тела скользить друг по другу.
Деформация (деформация)
Деформация определяется как «деформация твердого тела под действием напряжения».
- Нормальная деформация — удлинение или сжатие отрезка прямой
- Деформация сдвига — изменение угла между двумя отрезками прямой, изначально перпендикулярными
Нормальная деформация, которая может быть выражена как
= σ / е (3)
, где 1
dl = изменение длины (м, в)
l o = начальная длина (м, в)
ε = деформация — безразмерная
E = модуль Юнга (модуль упругости) (Па , (Н/м 2 ), фунт/кв.
Обратите внимание, что деформация является безразмерной единицей, поскольку она представляет собой отношение двух длин.Но также общепринято указывать это как отношение двух единиц длины — например, м/м или дюймов/дюйм .
Пример — Напряжение и изменение длины
Стержень в приведенном выше примере имеет длину 2 м и изготовлен из стали с модулем упругости 200 ГПа (200 10 9 Н/м 2 ) . Изменение длины можно рассчитать путем преобразования (3) в
dl = σ l o / E
= (1205 10
м 9 Па)
= 0.00127 м
= 1,27 мм
Энергия деформации
Напряжение объекта сохраняет в нем энергию. Для осевой нагрузки накопленная энергия может быть выражена как
U = 1/2 F n dl
, где
U = энергия деформации (Дж (Н·м), фут-фунт) 2
6 Модуль Юнга — модуль упругости (или модуль упругости) — закон Гука Большинство металлов деформируется пропорционально приложенной нагрузке в диапазоне нагрузок.Напряжение пропорционально нагрузке, а деформация пропорциональна деформации в соответствии с законом Гука .
E = Стресс / штамм
= σ / / ε
= (F N / A) / (DL / L O ) ( 4)
, где , где
E = Young Modulus (N / M 2 ) (LB / в 2 , PSI)
модуль упругости или модуля молодых, обычно используется для металлов и металлических сплавов и выражается в единицах 10 6 lb f /in 2 , Н/м 2 или Па .Модуль упругости при растяжении часто используется для пластмасс и выражается в терминах 10 5 фунтов f /in 2 или ГПа .
модуль сдвига эластичности — или модуль жесткости
г = стресс / штамм —
=
= τ / γ
= (f p / a) / (s / d) (5)
, где
G = модуль сдвига упругости — или модуль жесткости (N / M 2 ) (LB / в 2 , PSI)
τ = напряжение сдвига (PA) N / M 2 , PSI)
γ = Блок меньшее количество штамма сдвига
F p = сила, параллельная граням, на которые они действуют
A = площадь (м 2 , в 2 )
с = перемещение граней (м, дюйм)
6
11 ди расстояние между смещенными гранями (м, дюйм)
Объемный модуль упругости
Объемный модуль упругости — или объемный модуль — является мерой сопротивления вещества равномерному сжатию.
Объемный модуль упругости представляет собой отношение напряжения к изменению объема материала, подвергающегося осевой нагрузке.
Эластичные модули
Упругие модули для некоторых общих материалов:
Материал Young Moduls
9 — E —сдвиг модуль
— G —Объемный модуль
— K —+ (GPA)
(10 6 PSI)(GPA)
(GPA)
(10 6 PSI)(GPA)
(10 6 PSI )Алюминиевый 70 24 70 Латунь 91 36 61 Медь 110 42 140 Стекло 55 23 37 Железо 91 70 100 9044 7 Свинец 16 5. 6
70529 70529 70529 Сталь 200 8 9 80 160
- 1 GPA = 10 9 1000054 PA (N / M 2 )
- 10 6 psi = 1 Mpsi = 10 3 ksi
Напряжение и деформация – Приложение по сопротивлению материалов для энергетики1
Стресс-деформация
Цели обучения
После завершения этой главы вы сможете:
- Дайте определение нормальному и касательному напряжению и деформации и обсудите взаимосвязь между расчетным напряжением, пределом текучести и предельным напряжением
- Конструктивные элементы, работающие на растяжение, сжатие и сдвигающие нагрузки
- Определение деформации элементов при растяжении и сжатии
Механическое напряжение
В этом разделе обсуждается влияние механических нагрузок (сил), действующих на элементы.
В следующей главе будет рассмотрено влияние тепловых нагрузок (тепловое расширение).
Нормальные, растягивающие и сжимающие напряжения
Растяжение или сжатие в элементе создают нормальные напряжения; их называют «нормальными», потому что поперечное сечение, воспринимающее нагрузку, перпендикулярно (нормально) к направлению приложенных сил. Растягивающие и сжимающие напряжения рассчитываются с помощью:
Если стержень имеет переменное поперечное сечение, площадь, которая должна использоваться в расчетах, представляет собой минимальную площадь поперечного сечения; это даст вам максимальное напряжение в элементе, которое в конечном итоге будет определять конструкцию.
При сдвиге площадь поперечного сечения, воспринимающая нагрузку, параллельна направлению приложенных сил. Кроме того, при оценке площади сдвига необходимо учитывать, сколько поперечных сечений влияют на общую прочность сборки.
Например, если вы считаете, что штифт дверной петли подвергается сдвигающей нагрузке, вам нужно подсчитать, сколько поперечных сечений выдерживает нагрузку.
Формула для расчета напряжения сдвига такая же:
При штамповке область, которая сопротивляется сдвигу, имеет форму цилиндра для круглого отверстия (подумайте о формочке для печенья).Следовательно, площадь сдвига будет найдена путем умножения окружности формы на толщину пластины.
Обратите внимание:Глядя на рисунки из учебника, вы заметите, что указаны две силы. Это не означает, что сила, которую вы используете в формуле, равна (2 × Сила P), а просто указывает, что одна из них — это сила Действия, а вторая — Противодействие.
Деформация и модуль упругости
Элемент при растяжении или сжатии будет упруго деформироваться пропорционально, среди прочих параметров, исходной длине.Деформация, также называемая единичной деформацией, представляет собой безразмерный параметр, выражаемый как:
Если вы решите использовать отрицательное значение деформации сжатия (уменьшение длины), то вы также должны указать отрицательное значение эквивалентного напряжения сжатия.
Модуль упругости
Кривая напряжение-деформация создается на основе испытания на растяжение. В упругой области графика деформация прямо пропорциональна нагрузке. Разделив нагрузку на площадь поперечного сечения (постоянную) и деформацию на исходную длину (постоянную), можно получить графическое представление зависимости деформации от деформации.Стресс. Постоянное соотношение напряжения и деформации — это модуль Юнга или модуль упругости, свойство каждого материала.
Упругая деформация
Объединение двух приведенных выше соотношений для деформации и модуля упругости приводит к единой формуле для упругой деформации при растяжении или сжатии.
Это соотношение применимо к элементам с однородным поперечным сечением из однородного материала, подверженным растягивающим или сжимающим нагрузкам, которые приводят к напряжениям ниже пропорционального предела (прямая линия на кривой σ-ε).
Расчетное напряжение и коэффициенты безопасности
Эти темы были освещены в 1 st год Сопротивление материалов и представлены здесь в виде краткого обзора.
Элементы, подвергающиеся чрезмерному напряжению, могут выйти из строя из-за разрушения, когда фактическое рабочее напряжение превышает предельное напряжение, или из-за чрезмерной деформации, которая делает их неработоспособными. Рассмотрим тяжелую линию конденсата, которая провисает сверх допустимого предела, и, хотя она не ломается, фланцевые соединения на концах линий будут протечь из-за углового перемещения.
Расчетное напряжение, σ d , представляет собой максимальный уровень фактического/рабочего напряжения, который считается приемлемым с точки зрения безопасности. Расчетное напряжение определяется по:
Коэффициент безопасности выбирается проектировщиком на основе опыта, суждений И руководств/правил из соответствующих норм и стандартов на основе нескольких критериев, таких как риск получения травм, точность расчетных данных, вероятность, отраслевые стандарты и, что не менее важно, стоимость. . Стандарты коэффициентов безопасности были установлены инженерами-строителями на основе строгих оценок и подкреплены многолетним опытом.
Стандарты постоянно развиваются, отражая новую и улучшенную философию дизайна. Пример:
Дизайнерские кейсы
При решении задач учащиеся могут столкнуться с разными сценариями. Хотя теоретические концепции одинаковы, пути к окончательным ответам могут быть разными, как того требует каждый подход.
- Оценка того, является ли проект/конструкция безопасным или нет
- Дано: величина и распределение нагрузок, свойства материалов, форма и размеры элементов
- Найдите: фактическое напряжение и сравните с расчетным напряжением; в качестве альтернативы найдите коэффициент безопасности и решите, является ли он приемлемым на основе применимых стандартов
.- Выбор подходящего материала
- Дано: величина и распределение нагрузок, форма и размеры элементов
- Найти: какой тип или марка материала обеспечит прочность (предел текучести или предел прочности) большую, чем требуется, с учетом выбранного или заданного коэффициента безопасности
- Определение формы и размеров поперечного сечения элемента
- Дано: величина и распределение нагрузок, свойства материалов
- Найти: форму и размеры элемента так, чтобы фактическая площадь поперечного сечения была больше минимально необходимой.
- Оценка максимально допустимой нагрузки на компонент
- Дано: тип и распределение нагрузки, свойства материала, форма и размеры элементов
- Найти: максимальная величина нагрузки, которая приводит к приемлемому напряжению
Элементы из двух разных материалов
Бывают случаи, когда элемент при нормальных напряжениях изготавливается из двух (или более) материалов. Одной из целей таких задач является нахождение напряжения в каждом компоненте.
Например, у вас может быть короткая колонна из стальной трубы, заполненной бетоном, как показано на рисунке. Учитывая общую нагрузку, свойства материалов и геометрические размеры, мы должны найти индивидуальное напряжение в каждом компоненте.
И стальная труба, и бетонный сердечник работают вместе, поддерживая нагрузку, поэтому мы должны найти дополнительные соотношения, которые объединят две проблемы в одну. Обычно мы ищем:
- соотношение, описывающее распределение силы между двумя материалами
- отношение, которое коррелирует деформации каждого материала
Для этой конкретной проблемы мы можем сказать, что:
Уравнение 1: Общая нагрузка P = нагрузка на сталь P сталь + нагрузка на бетон P бетон
поэтому P = Напряжение сталь × Площадь сталь + Напряжение бетон × Площадь бетон
Уравнение 2: деформации обоих материалов одинаковы
поэтому Штамм сталь = Штамм бетон
Учитывая, что модуль упругости = напряжение/деформация, уравнение (2) дает связь между напряжением и упругостью обоих материалов
Подстановка этого последнего соотношения в уравнение (1) и решение для напряжения бетона приводит к следующему соотношению
Далее можно найти Stress сталь .
Обратите внимание, что в зависимости от задачи исходные два соотношения могут отличаться, поэтому каждый раз может потребоваться полный пошаговый вывод.
Разумные ответыПри решении задач на нормальное напряжение-деформацию, особенно в системе СИ, вы должны иметь возможность судить, разумны ли ваши ответы или нет.
Пример: Стержень из углеродистой стали 36 длиной 1 м и диаметром 20 мм (Свойства материалов в Приложении B, Таблица B2) подвешивает груз массой 6 тонн.Оцените напряжение и напряжение в стержне.
Обратите внимание, что обычно нагрузки указаны в кН, площадь поперечного сечения в 10 -3 м 2 , а результирующие напряжения в МПа.
Кроме того, поскольку модули упругости выражены в ГПа, деформация (безразмерная) будет находиться в диапазоне 10 -3 . Этот стержень растянется на 0,9 мм под заданной нагрузкой.
Назначенные проблемыПри решении данных вопросов необходимо пользоваться Приложением к учебнику.
Они являются ценными справочниками по свойствам материалов, геометрическим размерам и т. д.
Задача 1: Линия конденсата номинальным размером 152 мм, изготовленная из трубы из углеродистой стали сортамента 40, поддерживается подвесками с резьбовыми стержнями, расположенными на расстоянии 2,5 м от центра к центру. Вешалки из углеродистой стали, длиной 50 см, с диаметром основания 12 мм. Рассчитайте напряжение и деформацию подвесок. Используйте E=200 ГПа для материала подвески.
Проблема 2: В магазинном подъемном механизме используется скоба с 1/2-дюймовым штифтом.Если штифт изготовлен из стали A36, определите максимальную безопасную нагрузку, используя коэффициент безопасности 2,5, основанный на пределе текучести.
Проблема 3: Котел опирается на несколько коротких колонн, как показано на рисунке, изготовленных из серого чугуна класса 35. Каждая колонна выдерживает нагрузку 50 тонн. Требуемый запас прочности для этой конструкции равен 3.
Надежны ли колонны?
Используйте следующие размеры: A = 30 мм, B = 80 мм, C = 50 мм, D = 140 мм
Задача 4: На растянутый элемент фермы крыши действует нагрузка 25 тысяч фунтов.В конструкции используется уголок L2x2x1/4 сечением 0,944 дюйма 2 . Для строительных конструкций Американский институт стальных конструкций рекомендует использовать расчетное напряжение 0,60×S y . Используя таблицу B2 Приложения B, укажите подходящий стальной материал.
Задача 5: Гидравлический цилиндр со стяжной тягой, как показано на рисунке, изготовлен из 6-дюймовой трубы из нержавеющей стали сортамента 40 и длиной 15 дюймов. Шесть стяжек представляют собой стержни с резьбой 1/2-13 UNC с диаметром основания 0.4822 дюйма и шаг резьбы 13 TPI. При сборке цилиндра требуется зажимное усилие, эквивалентное одному полному обороту гайки из положения затяжки вручную.
Определить напряжение в цилиндре и в тягах.
Также рассчитайте деформацию каждого компонента, используя модуль упругости E ss = 28×10 6 фунтов на квадратный дюйм и E стержень = 30×10 6 фунтов на квадратный дюйм.
Проблема 6: Предложите одно улучшение в этой главе.
Механика материалов: деформация » Механика гибких конструкций
Штамм
До сих пор мы сосредоточились на напряжении в элементах конструкции. Когда вы прикладываете нагрузку к объекту, он деформируется . Подумайте о резиновой ленте: вы тянете за нее, и она становится длиннее — она растягивается . Деформация — это мера того, насколько сильно растянулся объект, а деформация — это отношение между деформацией и исходной длиной.
Думайте о деформации как о 90 033 процентах удлинения 90 034 — насколько больше (или меньше) становится объект после его загрузки.
Как и при напряжении, существует два типа деформаций, которым может подвергаться конструкция: 1. Нормальная деформация и 2. Деформация сдвига . Когда сила действует перпендикулярно (или «нормально») к поверхности объекта, она создает нормальное напряжение. Когда сила действует параллельно поверхности объекта, возникает напряжение сдвига.
Рассмотрим стержень, находящийся под одноосным растяжением.Стержень удлиняется под действием этого напряжения до новой длины, и нормальная деформация представляет собой отношение этой небольшой деформации к первоначальной длине стержня.
Деформация — это безразмерная мера того, насколько объект становится больше или меньше от приложенной нагрузки. Нормальная деформация происходит, когда удлинение объекта происходит в ответ на нормальное напряжение (т.
Механическое поведение материалове. перпендикулярно поверхности), и обозначается греческой буквой эпсилон. Положительное значение соответствует растяжению деформации, а отрицательное сжатию .Деформация сдвига возникает, когда деформация объекта является реакцией на напряжение сдвига (т. Е. Параллельно поверхности), и обозначается греческой буквой gamma .
Очевидно, что стресс и напряжение связаны. Напряжение и деформация связаны конститутивным законом , и мы можем определить их взаимосвязь экспериментально, измерив, какое усилие требуется для растяжения материала. Это измерение можно выполнить с помощью теста на растяжение . В простейшем случае, чем больше вы тянете за объект, тем больше он деформируется, и при малых значениях деформации эта зависимость является линейной. Эта линейная эластичная зависимость между напряжением и деформацией известна как закон Гука .
Если построить график зависимости напряжения от деформации, для небольших деформаций этот график будет линейным, а наклон линии будет свойством материала, известным как модуль упругости Юнга . Это значение может сильно варьироваться от 1 кПа для желе до 100 ГПа для стали.Для большинства технических материалов линейная область диаграммы напряжения-деформации возникает только при очень малых деформациях (<0,1%). В этом курсе мы сосредоточимся только на материалах, которые являются линейно-эластичными (т. е. подчиняются закону Гука) и изотропными (они ведут себя одинаково независимо от того, в каком направлении вы их тянете).
Из закона Гука и наших определений напряжения и деформации мы можем легко получить простое соотношение для деформации материала.
Интуитивно этот экзамен имеет смысл: приложите больше нагрузки, получите большую деформацию; приложите ту же нагрузку к более жесткому или толстому материалу, получите меньшую деформацию.
Если конструкция меняет форму или материал или по-разному нагружена в разных точках, то мы можем разделить эти множественные нагрузки, используя принцип суперпозиции .
Обобщенный закон Гука
На прошлом уроке мы начали узнавать о том, как связаны стресс и напряжение – через закон Гука. Но до этого момента мы рассматривали только очень упрощенную версию закона Гука: мы говорили только о напряжении или напряжении в одном направлении.В этом уроке мы рассмотрим обобщенный закон Гука для однородных, изотропных и упругих материалов, на которые действуют силы более чем по одной оси.
Прежде всего, даже простое вытягивание (или толкание) большинства материалов в одном направлении на самом деле вызывает деформацию во всех трех ортогональных направлениях .
Вернемся к первой иллюстрации напряжения. На этот раз мы учтем тот факт, что вытягивание объекта в осевом направлении вызывает его сжатие в поперечном направлении в поперечном направлении:
Таким образом, потянув за него в направлении x , он сожмется в направлениях y и z .Это свойство материала известно как коэффициент Пуассона , обозначается греческой буквой nu и определяется как:
Или, более математически, используя осевую нагрузку, показанную на изображении выше, мы можем записать это как уравнение:
Поскольку коэффициент Пуассона представляет собой отношение двух деформаций, а деформация безразмерна, коэффициент Пуассона также безразмерен. Коэффициент Пуассона является материальным свойством . Коэффициент Пуассона может принимать значения от -1 до 0.5. Для большинства технических материалов, например стали или алюминия, коэффициент Пуассона составляет около 0,3, а для каучуков коэффициент Пуассона составляет около 0,5, которые называются «несжимаемыми».
Несжимаемость просто означает, что на любую величину, которую вы сожмете в одном направлении, она расширится на такую же величину в других направлениях — следовательно, ее объем не изменится.
В последнее десятилетие было проведено очень интересное исследование по созданию структурированных материалов , в которых используются геометрия и упругая нестабильность (тема, которую мы кратко рассмотрим в следующей лекции) для создания ауксетических материалов — материалов с отрицательным коэффициентом Пуассона.Физически это означает, что когда вы тянете материал в одном направлении, он расширяется во всех направлениях (и наоборот):
Этот принцип можно применить и в 3D для создания расширяемых/складных оболочек:
Благодаря коэффициенту Пуассона у нас теперь есть уравнение, связывающее деформацию в направлении y или z с деформацией в направлении z.
Мы можем, в свою очередь, связать это обратно со стрессом с помощью закона Гука.Это важное замечание: натяжение объекта в одном направлении вызывает напряжение только в этом направлении , а вызывает напряжение во всех трех направлениях . Итак, sigma y = sigma z = 0. Выпишем деформации в направлениях y и z через напряжение в направлении x .
Помните, до этого момента мы рассматривали только одноосную деформацию . В действительности конструкции могут быть одновременно нагружены в нескольких направлениях, вызывая напряжение в этих направлениях.Полезный способ понять это — представить очень крошечный «кубик» материала внутри объекта. Этот куб может иметь напряжения , которые нормали к каждой поверхности , например:
Таким образом, приложение нагрузки в направлении x вызывает нормальное напряжение в этом направлении, и то же самое верно для нормальных напряжений в направлениях y и z .
И, как мы теперь знаем, напряжения в одном направлении вызывают деформации во всех трех направлениях .Итак, теперь мы включим эту идею в закон Гука и запишем уравнения для деформации в каждом направлении как:
Эти уравнения выглядят сложнее, чем они есть на самом деле: деформация в каждом направлении (или каждый компонент деформации) зависит от нормального напряжения в этом направлении, а коэффициент Пуассона умножается на деформацию в двух других направлениях. Теперь у нас есть уравнения того, как объект изменит форму в трех ортогональных направлениях. Ну, если объект меняет форму во всех трех направлениях, значит, он изменит свой объем на .Простую меру этого изменения объема можно найти, сложив три нормальных компонента деформации:
Теперь, когда у нас есть уравнение для изменения объема, или расширения , в терминах нормальных деформаций, мы можем переписать его в терминах нормальных напряжений.
Очень распространенный тип стресса, который вызывает дилатацию, известен как гидростатический стресс.
Это просто давление, которое одинаково действует на весь материал. Поскольку он действует одинаково, это означает:
Итак, в случае гидростатического давления мы можем сократить наше окончательное уравнение для расширения до следующего:
Это окончательное соотношение важно, потому что оно определяет, как объем материала изменяется под действием гидростатического давления.Предварительный коэффициент для p можно переписать как объемный модуль материала , K .
Наконец, вернемся к идее «несжимаемых» материалов. Что происходит с K — мерой того, как материал изменяет объем при заданном давлении, — если коэффициент Пуассона для материала равен 0,5?
Закон Гука при сдвигеВ предыдущем разделе мы разработали отношения между нормальным напряжением и нормальной деформацией.Теперь нам нужно поговорить о сдвиге. Вернемся к этому воображаемому кубу материала.
В дополнение к внешним силам, вызывающим напряжения, перпендикулярные каждой поверхности куба, силы могут вызывать напряжения, параллельные каждой грани куба. А, как известно, параллельные поперечному сечению напряжения равны касательных напряжений
Теперь этот куб материала выглядит намного сложнее, но на самом деле это не так уж и плохо. На каждой поверхности есть два напряжения сдвига, и нижние индексы говорят вам, в каком направлении они указывают и какой поверхности они параллельны.Например, возьмем правую грань куба. Напряжения, перпендикулярные этой поверхности, являются нормальными напряжениями в направлении x . Есть два напряжения, параллельных этой поверхности, одно указывает в направлении y (обозначается тау xy ), а другое указывает в направлении z (обозначается тау xz ). Чтобы куб находился в равновесии, тау х у = тау у х (иначе куб вращался бы). Таким образом, теперь имеется шести напряжений (сигма x , сигма, сигма, тау xy, тау yz, тау xz ), которые характеризуют напряженное состояние в однородном, изотропном, упругом материале.
Итак, как эти напряжения сдвига связаны с деформациями сдвига? Закон Гука при сдвиге очень похож на уравнение, которое мы видели для нормального напряжения и деформации:
В этом уравнении пропорция между напряжением сдвига и деформацией сдвига известна как модуль сдвига материала. Это уравнение в его общей форме, но мы можем переписать его более явно с точки зрения компонентов x, y и z . Это даст нам обобщенный закон Гука для однородных, изотропных, эластичных материалов.
В нашем обобщенном законе Гука у нас есть шесть компонентов напряжения и деформации и три свойства материала. Возникает естественный вопрос: как эти три свойства материала соотносятся друг с другом? Это отношение задается следующим уравнением:
СводкаВ этой лекции мы ввели понятие деформации. Деформация – это деформация материала от напряжения. Это просто отношение изменения длины к первоначальной длине.
Деформации, прикладываемые перпендикулярно поперечному сечению, представляют собой нормальных деформаций , а деформации, приложенные параллельно поперечному сечению, представляют собой деформации сдвига . Для линейных эластичных материалов напряжение линейно связано с деформацией по закону Гука. Пропорциональность этого отношения известна как модуль упругости материала . Используя закон Гука, мы можем записать простое уравнение, которое описывает, как материал деформируется под действием внешней нагрузки.
Кроме того, в этом разделе мы узнали о многоосевой нагрузке .В частности, мы узнали, что напряжение в одном направлении вызывает деформацию в трех направлениях . Это происходит из-за свойства материала, известного как коэффициент Пуассона – отношение между поперечной и осевой деформациями. Деформации, происходящие в трех ортогональных направлениях, могут дать нам меру расширения материала в ответ на многоосную нагрузку.
В частности, материал обычно может изменять объем в ответ на изменения внешнего давления или гидростатического напряжения .Это привело к определению устойчивости материалов к изменению объема под действием гидростатического напряжения – модуль объемного сжатия . Исследуя воображаемый кубический элемент в произвольном материале, мы смогли представить напряжения, возникающие перпендикулярно и параллельно каждой грани куба. Это дало нам шесть напряжений и шесть деформаций (три нормальных и три сдвиговых), которые мы соотнесли друг с другом с помощью обобщенного закона Гука для однородных , изотропных и упругих материалов.Эти компоненты многоосного напряжения и деформации связаны тремя свойствами материала: модулем упругости Юнга , модулем сдвига и коэффициентом Пуассона .
Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153.
Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального Научный фонд.
12.4: Напряжение, деформация и модуль упругости (часть 1)
Цели обучения
- Объяснять понятия напряжения и деформации при описании упругих деформаций материалов
- Описывать виды упругой деформации предметов и материалов
Модель твердого тела представляет собой идеализированный пример объекта, не деформирующегося под действием внешних сил. Это очень полезно при анализе механических систем, ведь многие физические объекты действительно в значительной степени жесткие.Степень, в которой объект может восприниматься как жесткий, зависит от физических свойств материала, из которого он сделан. Например, шарик для пинг-понга, сделанный из пластмассы, является хрупким, а теннисный мячик, сделанный из резины, упругим при воздействии сжимающих сил.
Однако при других обстоятельствах и мячик для пинг-понга, и мячик для тенниса могут хорошо отскакивать как твердые тела. Точно так же тот, кто проектирует протезы конечностей, может приблизиться к механике человеческих конечностей, моделируя их как твердые тела; однако фактическое сочетание костей и тканей представляет собой эластичную среду.
В оставшейся части этого раздела мы переходим от рассмотрения сил, влияющих на движение объекта, к тем, которые влияют на форму объекта. Изменение формы из-за приложения силы известно как деформация. Известно, что даже очень малые силы вызывают некоторую деформацию. Деформации подвергаются объекты или физические среды под действием внешних сил, например, это может быть раздавливание, сдавливание, разрывание, скручивание, разрезание или растяжение объектов. На языке физики два термина описывают силы, действующие на объекты, подвергающиеся деформации: напряжение и деформация .
Напряжение — это величина, описывающая величину сил, вызывающих деформацию.
Напряжение обычно определяется как силы на единицу площади . Когда силы притягивают объект и вызывают его удлинение, как растяжение эластичной ленты, мы называем такое напряжение растягивающим напряжением . Когда силы вызывают сжатие объекта, мы называем это сжимающим напряжением . Когда объект сдавливается со всех сторон, как подводная лодка в глубинах океана, мы называем этот вид напряжения объемным напряжением (или объемным напряжением ).В других ситуациях действующие силы могут быть ни растягивающими, ни сжимающими, но при этом вызывать заметную деформацию. Например, предположим, что вы крепко держите книгу между ладонями, затем одной рукой вы нажимаете и тянете переднюю обложку от себя, а другой рукой нажимаете и тянете заднюю обложку к себе. ты. В таком случае, когда деформирующие силы действуют по касательной к поверхности объекта, мы называем их «сдвиговыми» силами, а напряжение, которое они вызывают, называется напряжением сдвига .
{5}\; Па = 14,7\; psi \ldotp\]
Объект или среда под напряжением деформируются. Величина, описывающая эту деформацию, называется деформация . Деформация задается как частичное изменение либо длины (при растягивающем напряжении), либо объема (при объемном напряжении), либо геометрии (при сдвиговом напряжении). Следовательно, деформация является безразмерным числом. Деформация при растягивающем напряжении называется деформация растяжения , деформация при объемном напряжении называется объемная деформация (или объемная деформация ), а деформация, вызванная напряжением сдвига, называется деформация сдвига .
Чем больше напряжение, тем больше деформация; однако связь между деформацией и напряжением не обязательно должна быть линейной. Только когда напряжение достаточно низкое, вызываемая им деформация прямо пропорциональна величине напряжения. Константа пропорциональности в этом отношении называется модулем упругости .
.В линейном пределе низких значений напряжения общее отношение между напряжением и деформацией составляет
\[напряжение = (упругость\; модуль) \умножить на деформацию \ldotp \label{12.33}\]
Как видно из размерного анализа этого отношения, модуль упругости имеет ту же физическую единицу, что и напряжение, поскольку деформация безразмерна.
Мы также можем видеть из уравнения \ref{12.33}, что когда объект характеризуется большим значением модуля упругости, влияние напряжения невелико. С другой стороны, небольшой модуль упругости означает, что напряжение вызывает большую деформацию и заметную деформацию. Например, нагрузка на резиновую ленту вызывает большую деформацию (деформацию), чем такая же нагрузка на стальную ленту тех же размеров, поскольку модуль упругости резины на два порядка меньше модуля упругости стали.
Модуль упругости при растягивающем напряжении называется модулем Юнга ; объемное напряжение называется объемным модулем ; а то, что касается напряжения сдвига, называется модулем сдвига .
Обратите внимание, что связь между напряжением и деформацией является наблюдаемой связью, измеренной в лаборатории. Модули упругости для различных материалов измеряются в различных физических условиях, таких как переменная температура, и собираются в таблицах технических данных для справки (Таблица \(\PageIndex{1}\)).Эти таблицы являются ценным справочным материалом для промышленности и всех, кто занимается проектированием или строительством. В следующем разделе мы обсудим отношения деформация-напряжение за линейным пределом, представленным уравнением \ref{12.33}, во всем диапазоне значений напряжения до точки разрушения. В оставшейся части этого раздела мы изучаем линейный предел, выраженный уравнением \ref{12.33}.
Таблица \(\PageIndex{1}\): приблизительные модули упругости для выбранных материалов Материал Модуль Юнга × 10 10 Па Объемный модуль × 10 10 Па Модуль сдвига × 10 10 Па Алюминий 7. 0
7,5 2,5 Кость (растяжение) 1,6 0,8 8,0 Кость (компрессия) 0,9 Латунь 9,0 6,0 3,5 Кирпич 1. 5
Бетон 2,0 Медь 11,0 14,0 4,4 Краун 6,0 5,0 2,5 Гранит 4. 5
4,5 2,0 Волосы (человеческие) 1,0 Твердая древесина 1,5 1,0 Железо 21,0 16,0 7,7 Свинец 1. 6
4.1 0,6 Мрамор 6,0 7,0 2,0 Никель 21,0 17,0 7,8 Полистирол 3,0 Шелк 6. 0
Паутинная резьба 3,0 Сталь 20,0 16,0 7,5 Ацетон 0,07 Этанол 0. 09
Глицерин 0,45 Меркурий 2,5 Вода 0,22 Напряжение растяжения или сжатия, деформация и модуль Юнга
Растяжение или сжатие возникает, когда две антипараллельные силы одинаковой величины действуют на объект только в одном из его измерений таким образом, что объект не движется.
Один из способов представить такую ситуацию показан на рисунке \(\PageIndex{1}\). Отрезок стержня либо растягивается, либо сжимается парой сил, действующих по его длине и перпендикулярно поперечному сечению. Суммарное действие таких сил состоит в том, что стержень изменяет свою длину от первоначальной длины L 0 , которую он имел до появления сил, на новую длину L, которую он имеет под действием сил. Это изменение длины \(\Delta\)L = L − L 0 может быть либо удлинением (когда \(L\) больше исходной длины \(L_o\)) либо сокращением (когда L меньше исходная длина L 0 ).Растягивающее напряжение и деформация возникают, когда силы растягивают объект, вызывая его удлинение, а изменение длины \(\Delta L\) является положительным. Сжимающее напряжение и деформация возникают, когда силы сжимают объект, вызывая его укорочение, а изменение длины \(\Delta L\) отрицательно.
В любой из этих ситуаций мы определяем напряжение как отношение деформирующей силы \(F_{\perp}\) к площади поперечного сечения A деформируемого объекта.
Символ F \(\perp\) , который мы оставляем за деформирующей силой, означает, что эта сила действует перпендикулярно поперечному сечению объекта.Силы, действующие параллельно поперечному сечению, не изменяют длину объекта. Определение растягивающего напряжения
\[растяжение\; напряжение = \frac{F_{\perp}}{A} \ldotp \label{12.34}\]
Деформация при растяжении является мерой деформации объекта под действием растягивающего напряжения и определяется как частичное изменение длины объекта, когда объект подвергается растягивающему напряжению
\[растяжение\; деформация = \frac{\Delta L}{L_{0}} \ldotp \label{12.35}\]
Напряжение и деформация сжатия определяются по одним и тем же формулам, уравнения \ref{12.34} и \ref{12.35} соответственно. Единственное отличие от ситуации растяжения заключается в том, что для сжимающего напряжения и деформации мы берем абсолютные значения правых частей в уравнении \ref{12.34} и \ref{12.35}.
Рисунок \(\PageIndex{1}\): когда объект находится в состоянии растяжения или сжатия, результирующая сила, действующая на него, равна нулю, но объект деформируется, изменяя свою первоначальную длину L 0 .(a) Натяжение: стержень удлиняется на \(\Delta\)L. (b) Сжатие: стержень сжимается на \(\Delta\)L.В обоих случаях деформирующая сила действует по длине стержня и перпендикулярно его поперечному сечению. В линейном диапазоне малых напряжений площадь поперечного сечения стержня не изменяется.
Модуль Юнга \(Y\) — это модуль упругости, когда деформация вызвана напряжением растяжения или сжатия, и определяется уравнением \ref{12.33}. Разделив это уравнение на деформацию растяжения, получим выражение для модуля Юнга:
\[Y = \frac{растяжение\; стресс {растяжение \; деформация} = \ frac {\ frac {F _ {\ perp}} {A}} {\ frac {\ Delta L} {L_ {0}}} = \ frac {F _ {\ perp}} {A} = \ frac {L_{0}}{\Delta L} \ldotp \label{12.36}\]
Пример \(\PageIndex{1}\): напряжение сжатия в колонне
Скульптура весом 10 000 Н опирается на горизонтальную поверхность на вершине вертикальной колонны высотой 6,0 м. Рисунок \(\PageIndex{1}\). Площадь поперечного сечения столба 0,20 м 2 , он изготовлен из гранита с массовой плотностью 2700 кг/м 3 .
Рисунок \(\PageIndex{2}\): Колонна Нельсона на Трафальгарской площади, Лондон, Англия. (кредит: модификация работы Кристиана Бортеса)Найти напряжение сжатия в поперечном сечении, расположенном на 3,0 м ниже вершины целика, и величину деформации сжатия вершины 3.0-м сегмент целика.
Стратегия
Сначала находим вес верхней части стойки длиной 3,0 м. Нормальная сила, действующая на поперечное сечение, расположенное на расстоянии 3,0 м от вершины, представляет собой сумму веса столба и веса скульптуры. Получив нормальную силу, мы используем уравнение 12.34, чтобы найти напряжение. Чтобы найти деформацию сжатия, мы находим значение модуля Юнга для гранита в таблице \(\PageIndex{1}\) и инвертируем уравнение \ref{12.{-6} \ldotp\]
Значение
Обратите внимание, что нормальная сила, действующая на площадь поперечного сечения стойки, не постоянна по ее длине, а изменяется от наименьшего значения вверху до наибольшего значения внизу стойки.
Таким образом, если столб имеет одинаковую площадь поперечного сечения по всей длине, наибольшее напряжение приходится на его основание.
Упражнение \(\PageIndex{2}\)
Найдите сжимающее напряжение и деформацию в основании колонны Нельсона.
Пример \(\PageIndex{2}\): растягивание стержня
Стальной стержень длиной 2,0 м и площадью поперечного сечения 0,30 см 2 . Штанга представляет собой часть вертикальной опоры, удерживающей тяжелую 550-килограммовую платформу, прикрепленную к нижнему концу штанги. Чему равно растягивающее напряжение в стержне и удлинение стержня под действием напряжения без учета веса стержня?
Стратегия
Сначала мы вычисляем растягивающее напряжение в стержне под весом платформы в соответствии с уравнением 12.{-3}\; т = 1,8\; мм \ldotp\end{split}\]
Значение
Так же, как и в примере с колонной, растягивающее напряжение в этом примере неравномерно по длине стержня.
Однако, в отличие от предыдущего примера, если принять во внимание вес стержня, напряжение в стержне наибольшее в верхней части и наименьшее в нижней части стержня, к которому прикреплено оборудование.
Упражнение \(\PageIndex{2}\)
Проволока длиной 2,0 м тянется 1.0 мм под нагрузкой. Чему равна деформация растяжения в проволоке?
Объекты часто могут одновременно подвергаться как сжимающему, так и растягивающему напряжению. Рисунок \(\PageIndex{3}\). Одним из примеров является длинная полка, загруженная тяжелыми книгами, которая провисает между торцевыми опорами под весом книг. Верхняя поверхность полки находится в сжимающем напряжении, а нижняя поверхность полки в растягивающем напряжении. Точно так же длинные и тяжелые балки прогибаются под собственным весом. В современном строительстве такие деформации изгиба могут быть практически устранены при использовании двутавровых балок. Рисунок \(\PageIndex{4}\).
Рисунок \(\PageIndex{3}\): (a) Объект, изгибающийся вниз, испытывает растягивающее напряжение (растяжение) в верхней части и сжимающее напряжение (сжатие) в нижней части.(b) Элитные тяжелоатлеты часто временно сгибают железные стержни во время подъема, как, например, на Олимпийских играх 2012 года. (кредит b: модификация работы Александра Кочерженко) Рисунок \(\PageIndex{4}\): Стальные двутавровые балки используются в строительстве для уменьшения деформации изгиба. (кредит: модификация работы «Европейского округа инженерного корпуса армии США»/Flickr)
Моделирование
Тяжелый ящик стоит на столе, поддерживаемом тремя колоннами.Просмотрите эту демонстрацию, чтобы переместить блок, чтобы увидеть, как влияет сжатие (или растяжение) в столбцах, когда блок меняет свое положение.
Авторы и авторство
Сэмюэля Дж. Линга (Государственный университет Трумэна), Джеффа Санни (Университет Лойолы Мэримаунт) и Билла Мёбса с многими соавторами. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Разница между напряжением и деформацией в физике
Опубликовано Madhu
Ключевое различие между напряжением и деформацией в физике заключается в том, что напряжение — это сила, испытываемая объектом, которая вызывает изменение объекта, тогда как деформация — это изменение формы. объекта при приложении напряжения .
Напряжение и деформация в физике связаны друг с другом, и они прямо пропорциональны друг другу вплоть до предела упругости объекта. Связь между напряжением и деформацией можно определить с помощью закона Гука.
СОДЕРЖАНИЕ
1. Обзор и ключевые отличия
2. Что такое напряжение в физике
3. Что такое деформация в физике
4. Напряжение и деформация в табличной форме
5. Резюме сравненияЧто такое напряжение в физике?
Напряжение — это сила, испытываемая объектом, которая может вызвать изменение объекта.Это сила, приложенная к единице площади объекта. Мы можем дать ударение в физике следующим образом:
σ= F/A
Когда σ представляет собой напряжение, F представляет собой приложенную силу, а A представляет собой площадь приложения силы.
Единицей измерения напряжения является Н/м 2 . Существует два типа напряжения: это растягивающее напряжение и сжимающее напряжение. Растягивающее напряжение — это сила, действующая на единицу площади материала, которая может привести к увеличению длины объекта. Поэтому объекты, находящиеся под растягивающим напряжением, могут становиться тоньше и длиннее.
Напряжение в зависимости от деформации пластичного материала
Напряжение сжатия — это сила, действующая на единицу площади, которая может привести к уменьшению длины объекта. Поэтому объекты, находящиеся под этим напряжением, могут становиться толще и короче.
Что такое деформация в физике?
Деформация — это изменение формы объекта при приложении нагрузки. Следовательно, мы можем определить его как величину деформации, которую испытывает объект в соответствии с направлением приложенной силы, деленную на начальные размеры тела.Соотношение между этими терминами можно представить следующим образом:
ε= δл/л
ε — деформация, возникающая из-за напряжения, l — изменение длины, а L — первоначальная длина этого объекта.
Деформация объекта является безразмерным свойством (длина делится на другую длину). Мы можем придать ему относительное изменение формы.
Существует два типа деформации: деформация растяжения и деформация сжатия. Деформация растяжения возникает из-за напряжения растяжения, а деформация сжатия возникает из-за напряжения сжатия.
В чем разница между напряжением и деформацией в физике?
Напряжение и деформация в физике связаны друг с другом, и они прямо пропорциональны друг другу вплоть до предела упругости объекта. Связь между напряжением и деформацией можно определить с помощью закона Гука. Ключевое различие между напряжением и деформацией в физике заключается в том, что напряжение — это сила, испытываемая объектом, которая вызывает изменение объекта, тогда как деформация — это изменение формы объекта при приложении напряжения.При этом напряжение измеримо и имеет единицу измерения, а деформация — безразмерная величина и не имеет единицы измерения.
Ниже приведена сводка различий между напряжением и деформацией в табличной форме.
Сводка сравнения – напряжение и деформация в физике
Напряжение и деформация в физике связаны друг с другом, и они прямо пропорциональны друг другу вплоть до предела упругости объекта. Связь между этими двумя терминами можно определить с помощью закона Гука.Ключевое различие между напряжением и деформацией в физике заключается в том, что напряжение — это сила, испытываемая объектом, которая вызывает изменение объекта, тогда как деформация — это изменение формы объекта при приложении напряжения.
Артикул:
1. «Напряжение и деформация — определение, кривая напряжения-деформации, закон Гука, единицы СИ». BYJUS , BYJU’S, 24 февраля 2021 г., доступно здесь.
Изображение предоставлено:
1. «Стремительно-деформативный пластичный материал» по разбивке (CC BY-SA 3.0) через Commons Wikimedia
Что такое деформация, напряжение и коэффициент Пуассона?
- Тензодатчик
- Типы тензорезисторов
- Как выбрать тензодатчики
- Деформация, напряжение и коэффициент Пуассона
- Принципы тензодатчиков
- Принципы измерения деформации
- Система подключения тензодатчиков
- Датчики с автоматической температурной компенсацией
- Система кодирования названия модели тензорезистора
- Основные свойства тензодатчиков KYOWA
- Тензодатчики с предварительно прикрепленными токопроводящими кабелями
Когда на материал действует растягивающая сила P, в нем возникает напряжение, соответствующее приложенной силе.
Пропорционально напряжению поперечное сечение сжимается, а длина удлиняется на ΔL по сравнению с длиной L, которую материал имел до приложения растягивающей силы (см. иллюстрацию на рис. 1) ниже.
Отношение удлинения к первоначальной длине называется деформацией растяжения и выражается следующим образом:
См. нижний рисунок на рис. 1. Если на материал действует сжимающая сила, он испытывает сжимающую деформацию, выраженную следующим образом:Например, если сила растяжения заставляет материал длиной 100 мм удлиниться на 0.01 мм инициированная в материале деформация:
Таким образом, штамм является абсолютным числом и выражается числовым значением с x10 -6 штаммом, с суффиксом με или мкм/м.
На основании закона Гука соотношение между напряжением и деформацией, вызываемой в материале приложенной силой, выражается следующим образом:
Таким образом, напряжение получается путем умножения деформации на модуль Юнга. Когда на материал действует растягивающая сила P, он удлиняется в осевом направлении и сжимается в поперечном направлении.Удлинение в осевом направлении называется продольной деформацией, а сужение в поперечном направлении — поперечной деформацией. Абсолютное значение отношения между продольной деформацией и поперечной деформацией называется коэффициентом Пуассона, который выражается следующим образом:
Коэффициент Пуассона различается в зависимости от материала.Продукты, которые вы недавно проверяли
Инженерное напряжение/деформация против истинного напряжения/деформации – Yasin ÇAPAR
В машиностроении и материаловедении кривая напряжение-деформация для материала дает взаимосвязь между напряжением и деформацией.Это достигается путем постепенного приложения нагрузки к испытательному образцу и измерения деформации при испытаниях на растяжение, при которых можно определить напряжение и деформацию. Эти кривые показывают многие свойства материалов, такие как модуль Юнга, предел текучести, предел прочности при растяжении и так далее.
График напряжения/деформации эксперимента по испытанию на растяжение.Кривая напряжения-деформации для материала строится путем удлинения образца и записи изменения напряжения в зависимости от деформации до разрушения образца.Деформация отложена по горизонтальной оси, а напряжение отложена по вертикальной оси. Часто предполагается, что площадь поперечного сечения материала не изменяется в течение всего процесса деформации. Это неверно, так как фактическая площадь будет уменьшаться при деформации из-за упругой и пластической деформации. Кривая, основанная на исходном поперечном сечении и расчетной длине, называется инженерной кривой напряжения-деформации , а кривая, основанная на мгновенной площади поперечного сечения и длине, называется истинной кривой напряжения-деформации .
Для технических напряжений предполагается, что длина и диаметр образца остаются постоянными на протяжении всего эксперимента.
Инженерное напряжение рассчитывается по:
Инженерная деформация рассчитывается по:
Истинное напряжение – это приложенная нагрузка, деленная на фактическую площадь поперечного сечения (изменяющуюся во времени площадь) материала.
Инженерное напряжение — это приложенная нагрузка, деленная на исходную площадь поперечного сечения материала. Также известен как номинальное напряжение.
Это показывает, что поперечное сечение образца изменилось в процессе эксперимента.
Сечение не сохраняется постоянно и будет отличаться от заданного значения диаметра. Этот стресс называется истинным стрессом. Приложенная сила делится на площадь сечения в этот момент.
Прежде чем подробно рассмотреть истинное напряжение и деформацию, давайте вспомним об испытаниях на растяжение (испытание на растяжение).
Испытание на растяжениеИспытание на растяжение, также известное как испытание на растяжение, представляет собой фундаментальное материаловедение и техническое испытание, в ходе которого образец подвергается контролируемому натяжению до разрушения.
Свойства, которые непосредственно измеряются с помощью испытания на растяжение, включают предел прочности при растяжении, прочность на разрыв, максимальное удлинение и уменьшение площади.
Поведение при разрушенииИз этих измерений также можно определить некоторые свойства: модуль Юнга, коэффициент Пуассона, предел текучести и характеристики деформационного упрочнения. Испытание на одноосное растяжение наиболее часто используется для получения механических характеристик изотропных материалов. Для некоторых материалов используются двухосные испытания на растяжение. Основное различие между этими испытательными машинами заключается в том, как нагрузка прикладывается к материалам.
Поведение при разрушении рассматривается в рамках двух основных свойств материалов, которые называются пластичными и хрупкими материалами.
Пластичный материал:
Значительная пластическая деформация и поглощение энергии (вязкость) проявляются перед разрушением. Характерной особенностью пластичного материала является образование шейки перед разрушением материала.Хрупкий материал :
Перед разрушением проявляется небольшая пластическая деформация или поглощение энергии.Характеристика хрупких материалов отличается от пластичных материалов. Хрупкие материалы разрушаются без образования шейки.
Разные материалы демонстрируют разные поведения/тренды при одинаковых условиях нагрузки.
Более традиционные конструкционные материалы, такие как бетон под напряжением, стекло, металлы и сплавы, демонстрируют адекватную линейную зависимость между напряжением и деформацией до наступления предела текучести.Испытание на осевое растяжение и испытание на изгиб двух разных материалов:
А — пластичный материал, В — хрупкий материал.Истинное напряжение ( σ t ) и истинная деформация ( ε t ) используются для точного определения пластического поведения пластичных материалов с учетом фактических размеров.
Хрупкие материалы обычно разрушаются вскоре после текучести или даже в пределе текучести, в то время как сплавы и многие стали могут сильно пластически деформироваться перед разрушением.
Истинное напряжение и деформацияХарактеристики каждого материала следует выбирать на основе требований к применению и конструкции.
Истинные напряжения и деформации отличаются от инженерных напряжений и деформаций.
При испытании на растяжение истинное напряжение больше инженерного напряжения, а истинное напряжение меньше инженерного напряжения. Разница между истинными и инженерными напряжениями и деформациями будет увеличиваться при пластической деформации. При низких деформациях (в упругой области) различия между ними незначительны.
Истинное напряжение ( σ t ):
Истинное напряжение – это напряжение, определяемое мгновенной нагрузкой, действующей на мгновенную площадь поперечного сечения.
Истинная деформация ( ε t ):
Истинная деформация логарифмическая, инженерная деформация линейная. Однако это оказывается почти таким же для малой деформации из-за малых значений в разложении Тейлора.
Истинное напряжение и деформация могут быть выражены инженерным напряжением и деформацией.
Для истинного напряжения:Для истинной деформации:
Интегрировать обе стороны и применить граничное условие,
Напряжение и деформация в месте сужения могут быть выражены как:
В заключение
Инженерное напряжение — это приложенная нагрузка, деленная на исходную площадь поперечного сечения материала.Также известен как номинальное напряжение.
Истинное напряжение — это приложенная нагрузка, деленная на фактическую площадь поперечного сечения (изменяющуюся во времени площадь) образца при этой нагрузке
Инженерная деформация — это величина деформации материала на единицу длины при растяжении. контрольная работа. Также известна как номинальная деформация.
Истинная деформация равна натуральному логарифму отношения текущей длины к исходной длине.Во время фазы образования шейки истинное напряжение не уменьшается.Кроме того, результаты, полученные в результате испытаний на растяжение и сжатие, будут давать по существу один и тот же график при использовании истинного напряжения и истинной деформации. Инженеры создадут допустимое напряжение и допустимую деформацию в данном элементе, и они хотят использовать диаграмму, основанную на инженерном напряжении и инженерной деформации с площадью поперечного сечения A 0 и длиной L 0 члена в недеформированном состоянии.
Инженерное напряжение: σ = F/A 0
Инженерное напряжение получается путем деления F на площадь поперечного сечения A 0 деформированного образца.Инженерное напряжение становится очевидным в пластичных материалах после начала текучести, прямо пропорционально уменьшению силы ( F) во время фазы образования шейки.
Истинное напряжение: σ t = F/A
Наблюдается, что истинное напряжение ( σ t) , пропорциональное F и обратно пропорциональное A , продолжает увеличиваться до тех пор, пока не произойдет разрыв образца.
Инженерная деформация: ε = δ/L 0
Истинная деформация: ε t = ln (L/L10
10 20 9 9
Разделив каждое приращение Δ L расстояния между калибровочными метками на соответствующее значение L , получим элементарную деформацию:
Δ ε = Δ L /L 0
Суммируя значения Δ ε
ε t = ∑ Δ ε = ∑ Δ L /L
Σ = F / A 0 Инжиниринг напряжения Σ T = F / A True Riss ε = δ / L 0 9 Инженерные штамм ε T = LN (L / L 0 ) True Desim
F Fнагрузка A 0 0 0площадь поперечного сечения образец до деформации произошла A площадь поперечного сечения Нагрузка на нагрузку δ δобщее удлинение L 0 L 0 0Оригинальная ценность длины набора L последовательные значения длины, как это меняется Источники:
упрм.


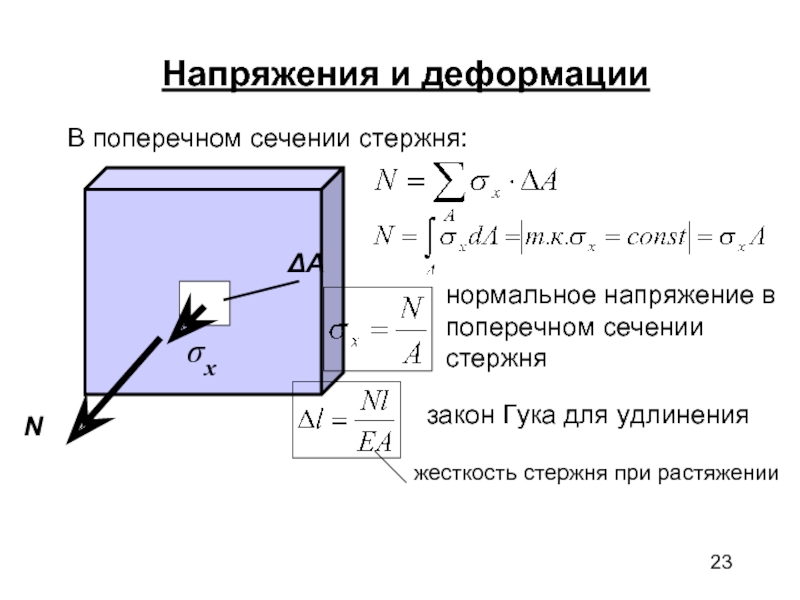 При этом в поперечном сечении стержней из шести коэффициентов внутренней силы имеется только один-продольная (осевая) сила N. простейший случай растяжения стержня и график продольной силы показаны
При этом в поперечном сечении стержней из шести коэффициентов внутренней силы имеется только один-продольная (осевая) сила N. простейший случай растяжения стержня и график продольной силы показаны Модуль упругости является одной из физических констант материала. Модуль упругости измеряется в единицах напряжения. 86 инвариантность модуля
Модуль упругости является одной из физических констант материала. Модуль упругости измеряется в единицах напряжения. 86 инвариантность модуля Чем больше металла было разогрето, тем наибольшие изменения происходят.
Чем больше металла было разогрето, тем наибольшие изменения происходят.
 2216 ньютонов (Н) = 4,4482216 килоньютонов (кН)
2216 ньютонов (Н) = 4,4482216 килоньютонов (кН)  Объемный модуль упругости представляет собой отношение напряжения к изменению объема материала, подвергающегося осевой нагрузке.
Объемный модуль упругости представляет собой отношение напряжения к изменению объема материала, подвергающегося осевой нагрузке. 6
6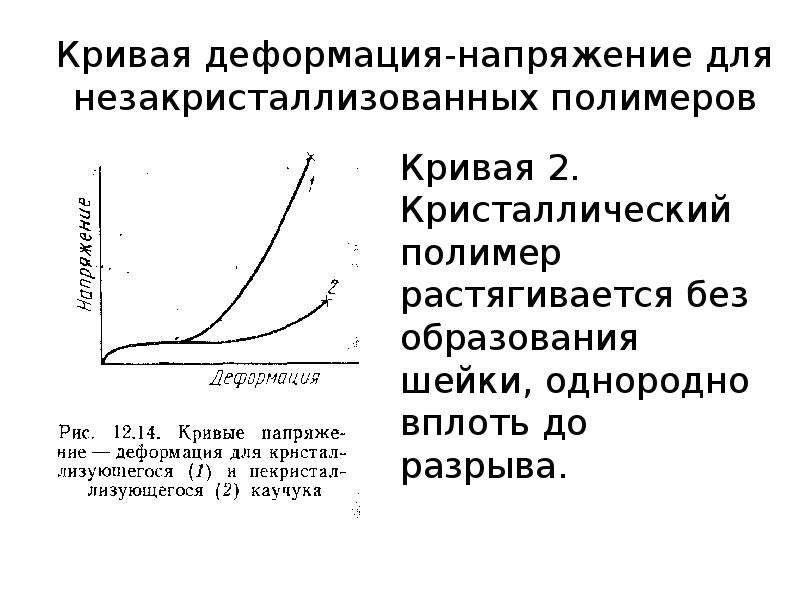 В следующей главе будет рассмотрено влияние тепловых нагрузок (тепловое расширение).
В следующей главе будет рассмотрено влияние тепловых нагрузок (тепловое расширение).
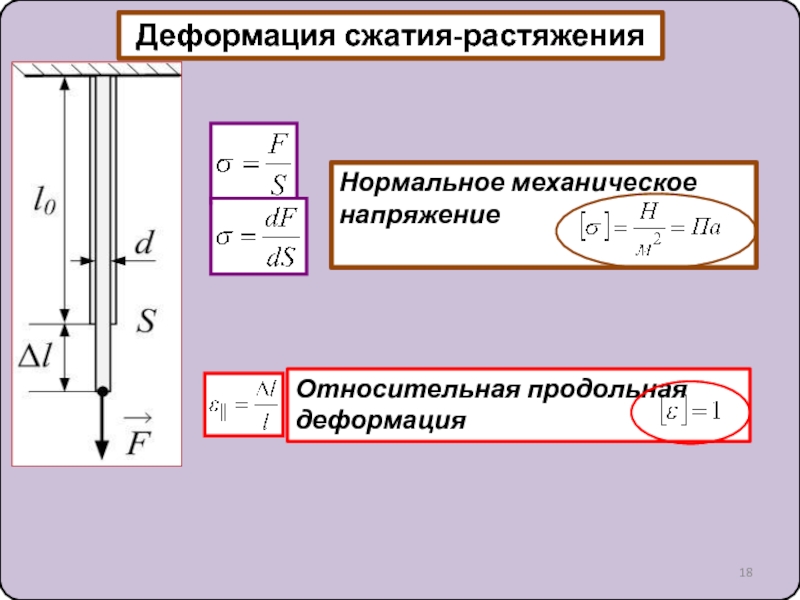
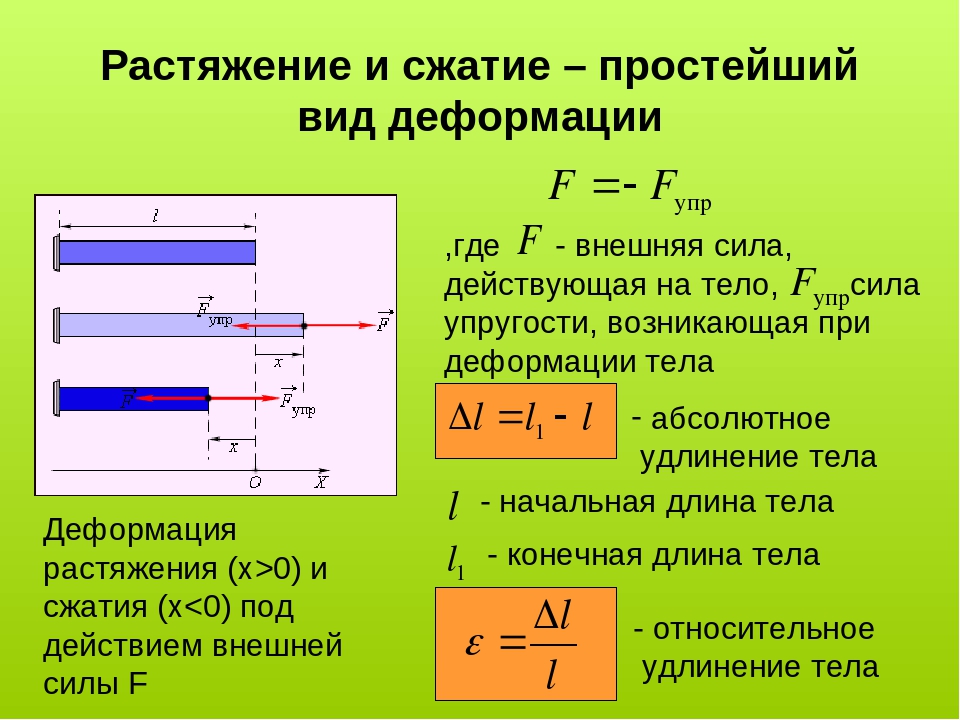
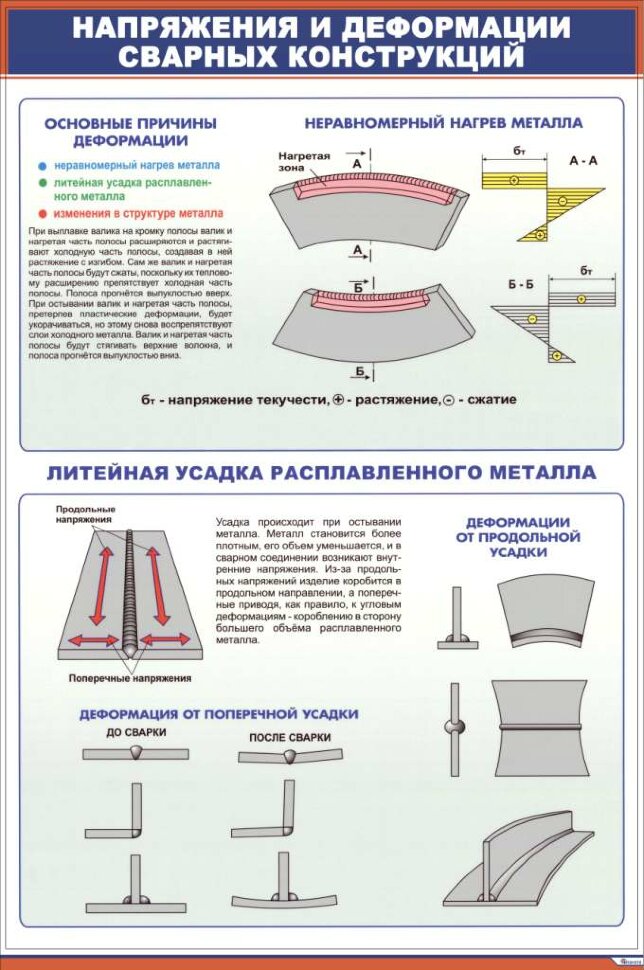 Стандарты постоянно развиваются, отражая новую и улучшенную философию дизайна. Пример:
Стандарты постоянно развиваются, отражая новую и улучшенную философию дизайна. Пример:

 Они являются ценными справочниками по свойствам материалов, геометрическим размерам и т. д.
Они являются ценными справочниками по свойствам материалов, геометрическим размерам и т. д.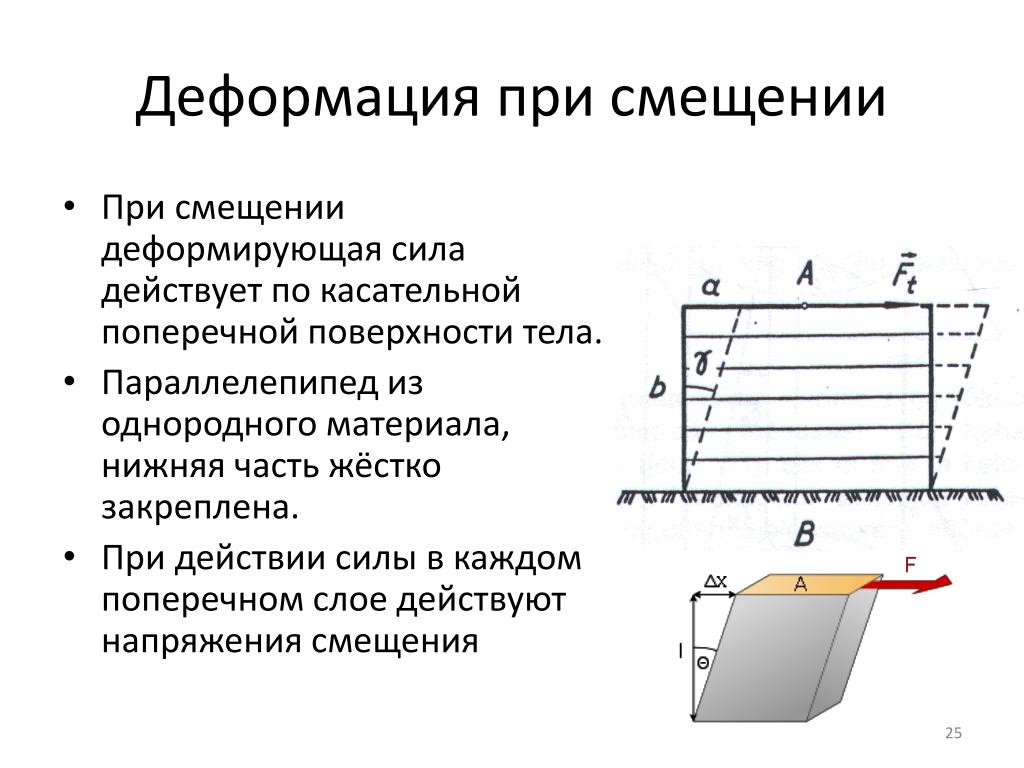 Надежны ли колонны?
Надежны ли колонны?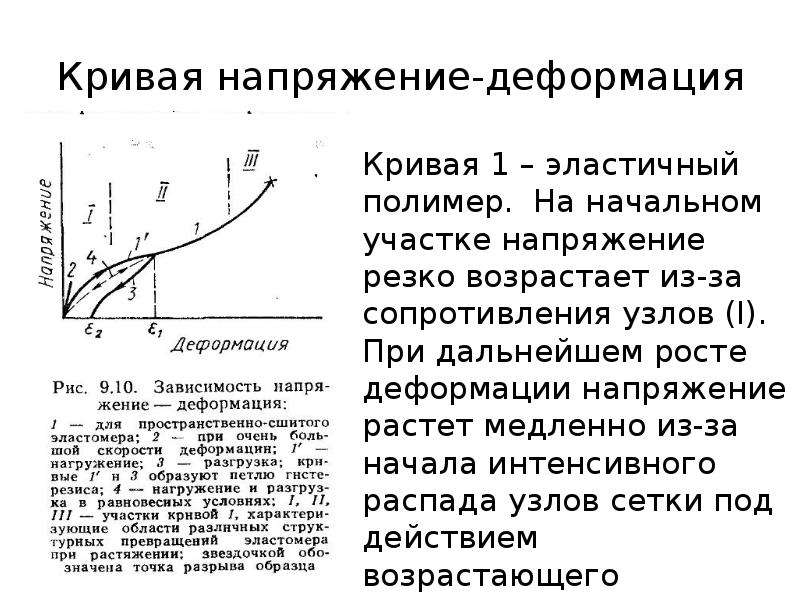 Также рассчитайте деформацию каждого компонента, используя модуль упругости E ss = 28×10 6 фунтов на квадратный дюйм и E стержень = 30×10 6 фунтов на квадратный дюйм.
Также рассчитайте деформацию каждого компонента, используя модуль упругости E ss = 28×10 6 фунтов на квадратный дюйм и E стержень = 30×10 6 фунтов на квадратный дюйм. Думайте о деформации как о 90 033 процентах удлинения 90 034 — насколько больше (или меньше) становится объект после его загрузки.
Думайте о деформации как о 90 033 процентах удлинения 90 034 — насколько больше (или меньше) становится объект после его загрузки. е. перпендикулярно поверхности), и обозначается греческой буквой эпсилон. Положительное значение соответствует растяжению деформации, а отрицательное сжатию .Деформация сдвига возникает, когда деформация объекта является реакцией на напряжение сдвига (т. Е. Параллельно поверхности), и обозначается греческой буквой gamma .
е. перпендикулярно поверхности), и обозначается греческой буквой эпсилон. Положительное значение соответствует растяжению деформации, а отрицательное сжатию .Деформация сдвига возникает, когда деформация объекта является реакцией на напряжение сдвига (т. Е. Параллельно поверхности), и обозначается греческой буквой gamma . Если построить график зависимости напряжения от деформации, для небольших деформаций этот график будет линейным, а наклон линии будет свойством материала, известным как модуль упругости Юнга . Это значение может сильно варьироваться от 1 кПа для желе до 100 ГПа для стали.Для большинства технических материалов линейная область диаграммы напряжения-деформации возникает только при очень малых деформациях (<0,1%). В этом курсе мы сосредоточимся только на материалах, которые являются линейно-эластичными (т. е. подчиняются закону Гука) и изотропными (они ведут себя одинаково независимо от того, в каком направлении вы их тянете).
Если построить график зависимости напряжения от деформации, для небольших деформаций этот график будет линейным, а наклон линии будет свойством материала, известным как модуль упругости Юнга . Это значение может сильно варьироваться от 1 кПа для желе до 100 ГПа для стали.Для большинства технических материалов линейная область диаграммы напряжения-деформации возникает только при очень малых деформациях (<0,1%). В этом курсе мы сосредоточимся только на материалах, которые являются линейно-эластичными (т. е. подчиняются закону Гука) и изотропными (они ведут себя одинаково независимо от того, в каком направлении вы их тянете). Если конструкция меняет форму или материал или по-разному нагружена в разных точках, то мы можем разделить эти множественные нагрузки, используя принцип суперпозиции .
Если конструкция меняет форму или материал или по-разному нагружена в разных точках, то мы можем разделить эти множественные нагрузки, используя принцип суперпозиции . Вернемся к первой иллюстрации напряжения. На этот раз мы учтем тот факт, что вытягивание объекта в осевом направлении вызывает его сжатие в поперечном направлении в поперечном направлении:
Вернемся к первой иллюстрации напряжения. На этот раз мы учтем тот факт, что вытягивание объекта в осевом направлении вызывает его сжатие в поперечном направлении в поперечном направлении: Несжимаемость просто означает, что на любую величину, которую вы сожмете в одном направлении, она расширится на такую же величину в других направлениях — следовательно, ее объем не изменится.
Несжимаемость просто означает, что на любую величину, которую вы сожмете в одном направлении, она расширится на такую же величину в других направлениях — следовательно, ее объем не изменится. Мы можем, в свою очередь, связать это обратно со стрессом с помощью закона Гука.Это важное замечание: натяжение объекта в одном направлении вызывает напряжение только в этом направлении , а вызывает напряжение во всех трех направлениях . Итак, sigma y = sigma z = 0. Выпишем деформации в направлениях y и z через напряжение в направлении x .
Мы можем, в свою очередь, связать это обратно со стрессом с помощью закона Гука.Это важное замечание: натяжение объекта в одном направлении вызывает напряжение только в этом направлении , а вызывает напряжение во всех трех направлениях . Итак, sigma y = sigma z = 0. Выпишем деформации в направлениях y и z через напряжение в направлении x . И, как мы теперь знаем, напряжения в одном направлении вызывают деформации во всех трех направлениях .Итак, теперь мы включим эту идею в закон Гука и запишем уравнения для деформации в каждом направлении как:
И, как мы теперь знаем, напряжения в одном направлении вызывают деформации во всех трех направлениях .Итак, теперь мы включим эту идею в закон Гука и запишем уравнения для деформации в каждом направлении как: Это просто давление, которое одинаково действует на весь материал. Поскольку он действует одинаково, это означает:
Это просто давление, которое одинаково действует на весь материал. Поскольку он действует одинаково, это означает: В дополнение к внешним силам, вызывающим напряжения, перпендикулярные каждой поверхности куба, силы могут вызывать напряжения, параллельные каждой грани куба. А, как известно, параллельные поперечному сечению напряжения равны касательных напряжений
В дополнение к внешним силам, вызывающим напряжения, перпендикулярные каждой поверхности куба, силы могут вызывать напряжения, параллельные каждой грани куба. А, как известно, параллельные поперечному сечению напряжения равны касательных напряжений 
 Деформации, прикладываемые перпендикулярно поперечному сечению, представляют собой нормальных деформаций , а деформации, приложенные параллельно поперечному сечению, представляют собой деформации сдвига . Для линейных эластичных материалов напряжение линейно связано с деформацией по закону Гука. Пропорциональность этого отношения известна как модуль упругости материала . Используя закон Гука, мы можем записать простое уравнение, которое описывает, как материал деформируется под действием внешней нагрузки.
Деформации, прикладываемые перпендикулярно поперечному сечению, представляют собой нормальных деформаций , а деформации, приложенные параллельно поперечному сечению, представляют собой деформации сдвига . Для линейных эластичных материалов напряжение линейно связано с деформацией по закону Гука. Пропорциональность этого отношения известна как модуль упругости материала . Используя закон Гука, мы можем записать простое уравнение, которое описывает, как материал деформируется под действием внешней нагрузки. В частности, материал обычно может изменять объем в ответ на изменения внешнего давления или гидростатического напряжения .Это привело к определению устойчивости материалов к изменению объема под действием гидростатического напряжения – модуль объемного сжатия . Исследуя воображаемый кубический элемент в произвольном материале, мы смогли представить напряжения, возникающие перпендикулярно и параллельно каждой грани куба. Это дало нам шесть напряжений и шесть деформаций (три нормальных и три сдвиговых), которые мы соотнесли друг с другом с помощью обобщенного закона Гука для однородных , изотропных и упругих материалов.Эти компоненты многоосного напряжения и деформации связаны тремя свойствами материала: модулем упругости Юнга , модулем сдвига и коэффициентом Пуассона .
В частности, материал обычно может изменять объем в ответ на изменения внешнего давления или гидростатического напряжения .Это привело к определению устойчивости материалов к изменению объема под действием гидростатического напряжения – модуль объемного сжатия . Исследуя воображаемый кубический элемент в произвольном материале, мы смогли представить напряжения, возникающие перпендикулярно и параллельно каждой грани куба. Это дало нам шесть напряжений и шесть деформаций (три нормальных и три сдвиговых), которые мы соотнесли друг с другом с помощью обобщенного закона Гука для однородных , изотропных и упругих материалов.Эти компоненты многоосного напряжения и деформации связаны тремя свойствами материала: модулем упругости Юнга , модулем сдвига и коэффициентом Пуассона .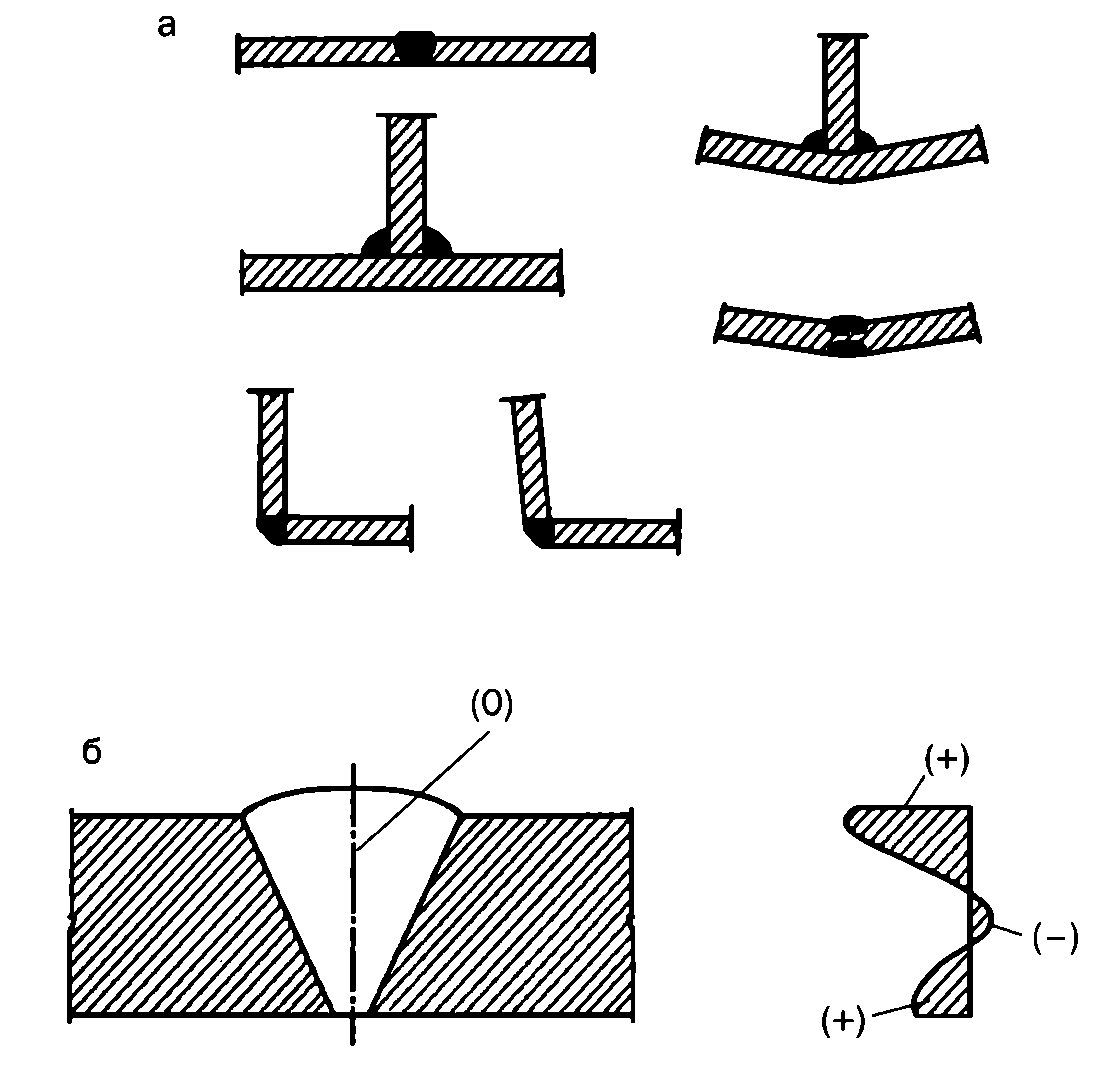 Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального Научный фонд.
Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального Научный фонд. Однако при других обстоятельствах и мячик для пинг-понга, и мячик для тенниса могут хорошо отскакивать как твердые тела. Точно так же тот, кто проектирует протезы конечностей, может приблизиться к механике человеческих конечностей, моделируя их как твердые тела; однако фактическое сочетание костей и тканей представляет собой эластичную среду.
Однако при других обстоятельствах и мячик для пинг-понга, и мячик для тенниса могут хорошо отскакивать как твердые тела. Точно так же тот, кто проектирует протезы конечностей, может приблизиться к механике человеческих конечностей, моделируя их как твердые тела; однако фактическое сочетание костей и тканей представляет собой эластичную среду. Напряжение обычно определяется как силы на единицу площади . Когда силы притягивают объект и вызывают его удлинение, как растяжение эластичной ленты, мы называем такое напряжение растягивающим напряжением . Когда силы вызывают сжатие объекта, мы называем это сжимающим напряжением . Когда объект сдавливается со всех сторон, как подводная лодка в глубинах океана, мы называем этот вид напряжения объемным напряжением (или объемным напряжением ).В других ситуациях действующие силы могут быть ни растягивающими, ни сжимающими, но при этом вызывать заметную деформацию. Например, предположим, что вы крепко держите книгу между ладонями, затем одной рукой вы нажимаете и тянете переднюю обложку от себя, а другой рукой нажимаете и тянете заднюю обложку к себе. ты. В таком случае, когда деформирующие силы действуют по касательной к поверхности объекта, мы называем их «сдвиговыми» силами, а напряжение, которое они вызывают, называется напряжением сдвига .
Напряжение обычно определяется как силы на единицу площади . Когда силы притягивают объект и вызывают его удлинение, как растяжение эластичной ленты, мы называем такое напряжение растягивающим напряжением . Когда силы вызывают сжатие объекта, мы называем это сжимающим напряжением . Когда объект сдавливается со всех сторон, как подводная лодка в глубинах океана, мы называем этот вид напряжения объемным напряжением (или объемным напряжением ).В других ситуациях действующие силы могут быть ни растягивающими, ни сжимающими, но при этом вызывать заметную деформацию. Например, предположим, что вы крепко держите книгу между ладонями, затем одной рукой вы нажимаете и тянете переднюю обложку от себя, а другой рукой нажимаете и тянете заднюю обложку к себе. ты. В таком случае, когда деформирующие силы действуют по касательной к поверхности объекта, мы называем их «сдвиговыми» силами, а напряжение, которое они вызывают, называется напряжением сдвига . {5}\; Па = 14,7\; psi \ldotp\]
{5}\; Па = 14,7\; psi \ldotp\] В линейном пределе низких значений напряжения общее отношение между напряжением и деформацией составляет
В линейном пределе низких значений напряжения общее отношение между напряжением и деформацией составляет Обратите внимание, что связь между напряжением и деформацией является наблюдаемой связью, измеренной в лаборатории. Модули упругости для различных материалов измеряются в различных физических условиях, таких как переменная температура, и собираются в таблицах технических данных для справки (Таблица \(\PageIndex{1}\)).Эти таблицы являются ценным справочным материалом для промышленности и всех, кто занимается проектированием или строительством. В следующем разделе мы обсудим отношения деформация-напряжение за линейным пределом, представленным уравнением \ref{12.33}, во всем диапазоне значений напряжения до точки разрушения. В оставшейся части этого раздела мы изучаем линейный предел, выраженный уравнением \ref{12.33}.
Обратите внимание, что связь между напряжением и деформацией является наблюдаемой связью, измеренной в лаборатории. Модули упругости для различных материалов измеряются в различных физических условиях, таких как переменная температура, и собираются в таблицах технических данных для справки (Таблица \(\PageIndex{1}\)).Эти таблицы являются ценным справочным материалом для промышленности и всех, кто занимается проектированием или строительством. В следующем разделе мы обсудим отношения деформация-напряжение за линейным пределом, представленным уравнением \ref{12.33}, во всем диапазоне значений напряжения до точки разрушения. В оставшейся части этого раздела мы изучаем линейный предел, выраженный уравнением \ref{12.33}. 0
0 5
5 5
5 6
6 0
0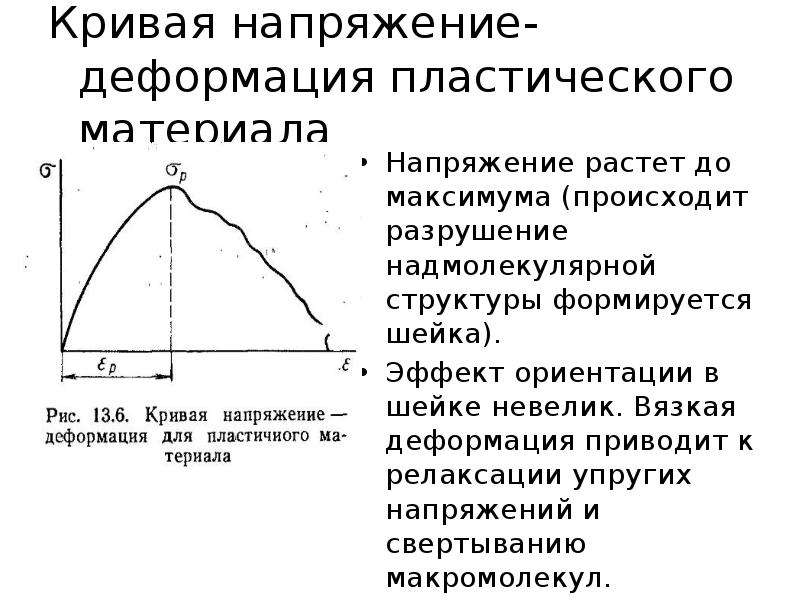 09
09 Один из способов представить такую ситуацию показан на рисунке \(\PageIndex{1}\). Отрезок стержня либо растягивается, либо сжимается парой сил, действующих по его длине и перпендикулярно поперечному сечению. Суммарное действие таких сил состоит в том, что стержень изменяет свою длину от первоначальной длины L 0 , которую он имел до появления сил, на новую длину L, которую он имеет под действием сил. Это изменение длины \(\Delta\)L = L − L 0 может быть либо удлинением (когда \(L\) больше исходной длины \(L_o\)) либо сокращением (когда L меньше исходная длина L 0 ).Растягивающее напряжение и деформация возникают, когда силы растягивают объект, вызывая его удлинение, а изменение длины \(\Delta L\) является положительным. Сжимающее напряжение и деформация возникают, когда силы сжимают объект, вызывая его укорочение, а изменение длины \(\Delta L\) отрицательно.
Один из способов представить такую ситуацию показан на рисунке \(\PageIndex{1}\). Отрезок стержня либо растягивается, либо сжимается парой сил, действующих по его длине и перпендикулярно поперечному сечению. Суммарное действие таких сил состоит в том, что стержень изменяет свою длину от первоначальной длины L 0 , которую он имел до появления сил, на новую длину L, которую он имеет под действием сил. Это изменение длины \(\Delta\)L = L − L 0 может быть либо удлинением (когда \(L\) больше исходной длины \(L_o\)) либо сокращением (когда L меньше исходная длина L 0 ).Растягивающее напряжение и деформация возникают, когда силы растягивают объект, вызывая его удлинение, а изменение длины \(\Delta L\) является положительным. Сжимающее напряжение и деформация возникают, когда силы сжимают объект, вызывая его укорочение, а изменение длины \(\Delta L\) отрицательно. Символ F \(\perp\) , который мы оставляем за деформирующей силой, означает, что эта сила действует перпендикулярно поперечному сечению объекта.Силы, действующие параллельно поперечному сечению, не изменяют длину объекта. Определение растягивающего напряжения
Символ F \(\perp\) , который мы оставляем за деформирующей силой, означает, что эта сила действует перпендикулярно поперечному сечению объекта.Силы, действующие параллельно поперечному сечению, не изменяют длину объекта. Определение растягивающего напряжения (a) Натяжение: стержень удлиняется на \(\Delta\)L. (b) Сжатие: стержень сжимается на \(\Delta\)L.В обоих случаях деформирующая сила действует по длине стержня и перпендикулярно его поперечному сечению. В линейном диапазоне малых напряжений площадь поперечного сечения стержня не изменяется.
(a) Натяжение: стержень удлиняется на \(\Delta\)L. (b) Сжатие: стержень сжимается на \(\Delta\)L.В обоих случаях деформирующая сила действует по длине стержня и перпендикулярно его поперечному сечению. В линейном диапазоне малых напряжений площадь поперечного сечения стержня не изменяется. Найти напряжение сжатия в поперечном сечении, расположенном на 3,0 м ниже вершины целика, и величину деформации сжатия вершины 3.0-м сегмент целика.
Найти напряжение сжатия в поперечном сечении, расположенном на 3,0 м ниже вершины целика, и величину деформации сжатия вершины 3.0-м сегмент целика. Таким образом, если столб имеет одинаковую площадь поперечного сечения по всей длине, наибольшее напряжение приходится на его основание.
Таким образом, если столб имеет одинаковую площадь поперечного сечения по всей длине, наибольшее напряжение приходится на его основание. Однако, в отличие от предыдущего примера, если принять во внимание вес стержня, напряжение в стержне наибольшее в верхней части и наименьшее в нижней части стержня, к которому прикреплено оборудование.
Однако, в отличие от предыдущего примера, если принять во внимание вес стержня, напряжение в стержне наибольшее в верхней части и наименьшее в нижней части стержня, к которому прикреплено оборудование.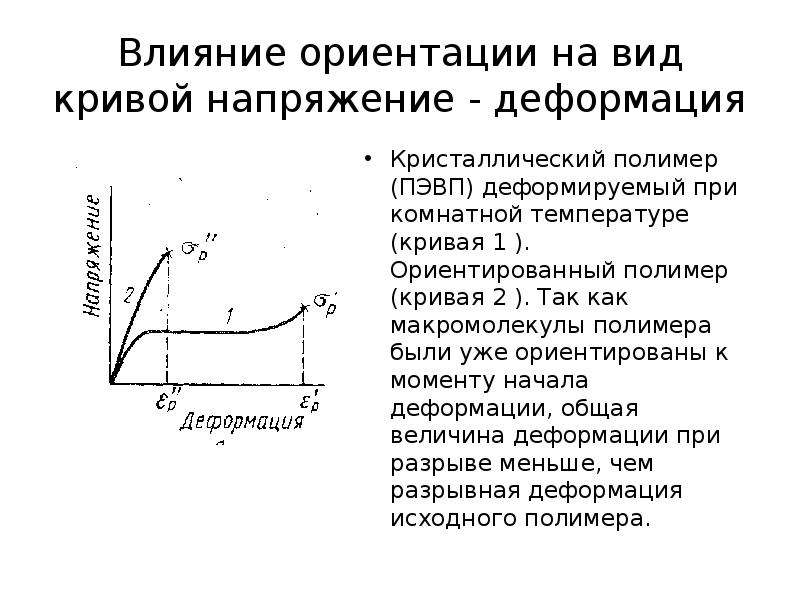 (b) Элитные тяжелоатлеты часто временно сгибают железные стержни во время подъема, как, например, на Олимпийских играх 2012 года. (кредит b: модификация работы Александра Кочерженко) Рисунок \(\PageIndex{4}\): Стальные двутавровые балки используются в строительстве для уменьшения деформации изгиба. (кредит: модификация работы «Европейского округа инженерного корпуса армии США»/Flickr)
(b) Элитные тяжелоатлеты часто временно сгибают железные стержни во время подъема, как, например, на Олимпийских играх 2012 года. (кредит b: модификация работы Александра Кочерженко) Рисунок \(\PageIndex{4}\): Стальные двутавровые балки используются в строительстве для уменьшения деформации изгиба. (кредит: модификация работы «Европейского округа инженерного корпуса армии США»/Flickr) Единицей измерения напряжения является Н/м 2 . Существует два типа напряжения: это растягивающее напряжение и сжимающее напряжение. Растягивающее напряжение — это сила, действующая на единицу площади материала, которая может привести к увеличению длины объекта. Поэтому объекты, находящиеся под растягивающим напряжением, могут становиться тоньше и длиннее.
Единицей измерения напряжения является Н/м 2 . Существует два типа напряжения: это растягивающее напряжение и сжимающее напряжение. Растягивающее напряжение — это сила, действующая на единицу площади материала, которая может привести к увеличению длины объекта. Поэтому объекты, находящиеся под растягивающим напряжением, могут становиться тоньше и длиннее. Деформация объекта является безразмерным свойством (длина делится на другую длину). Мы можем придать ему относительное изменение формы.
Деформация объекта является безразмерным свойством (длина делится на другую длину). Мы можем придать ему относительное изменение формы.
 Пропорционально напряжению поперечное сечение сжимается, а длина удлиняется на ΔL по сравнению с длиной L, которую материал имел до приложения растягивающей силы (см. иллюстрацию на рис. 1) ниже.
Пропорционально напряжению поперечное сечение сжимается, а длина удлиняется на ΔL по сравнению с длиной L, которую материал имел до приложения растягивающей силы (см. иллюстрацию на рис. 1) ниже.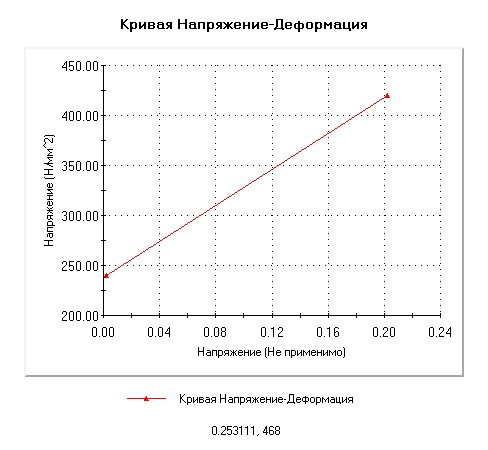 Удлинение в осевом направлении называется продольной деформацией, а сужение в поперечном направлении — поперечной деформацией. Абсолютное значение отношения между продольной деформацией и поперечной деформацией называется коэффициентом Пуассона, который выражается следующим образом:
Удлинение в осевом направлении называется продольной деформацией, а сужение в поперечном направлении — поперечной деформацией. Абсолютное значение отношения между продольной деформацией и поперечной деформацией называется коэффициентом Пуассона, который выражается следующим образом: 
 Инженерное напряжение — это приложенная нагрузка, деленная на исходную площадь поперечного сечения материала. Также известен как номинальное напряжение.
Инженерное напряжение — это приложенная нагрузка, деленная на исходную площадь поперечного сечения материала. Также известен как номинальное напряжение.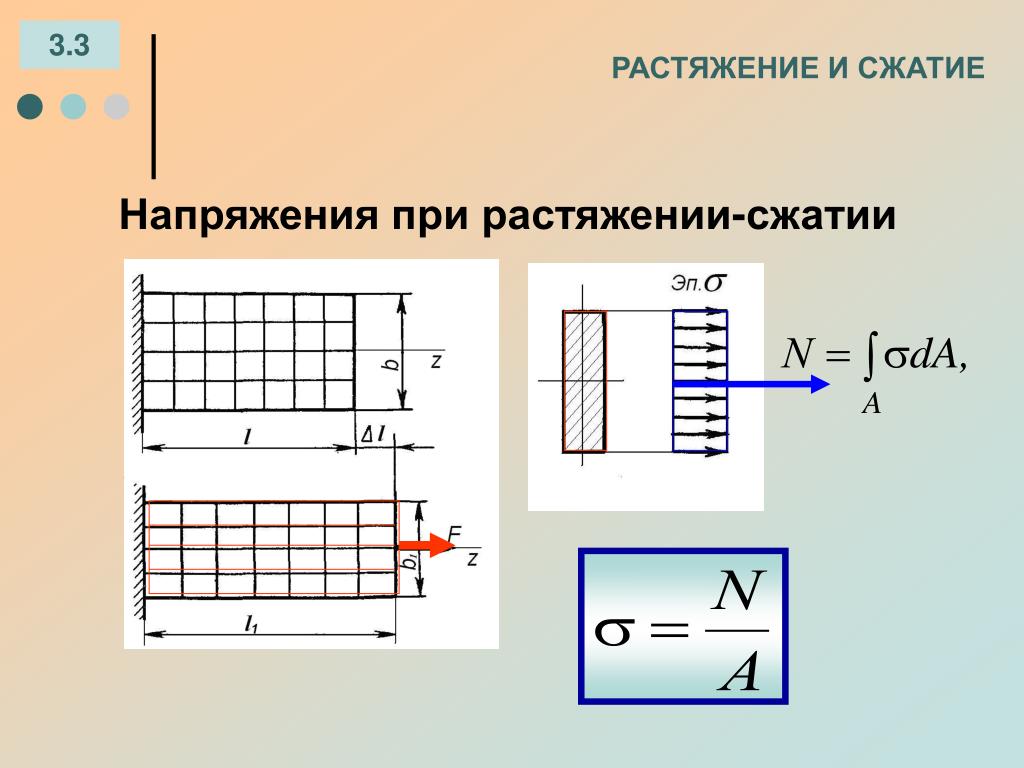 Из этих измерений также можно определить некоторые свойства: модуль Юнга, коэффициент Пуассона, предел текучести и характеристики деформационного упрочнения. Испытание на одноосное растяжение наиболее часто используется для получения механических характеристик изотропных материалов. Для некоторых материалов используются двухосные испытания на растяжение. Основное различие между этими испытательными машинами заключается в том, как нагрузка прикладывается к материалам.
Из этих измерений также можно определить некоторые свойства: модуль Юнга, коэффициент Пуассона, предел текучести и характеристики деформационного упрочнения. Испытание на одноосное растяжение наиболее часто используется для получения механических характеристик изотропных материалов. Для некоторых материалов используются двухосные испытания на растяжение. Основное различие между этими испытательными машинами заключается в том, как нагрузка прикладывается к материалам. Характеристика хрупких материалов отличается от пластичных материалов. Хрупкие материалы разрушаются без образования шейки.
Характеристика хрупких материалов отличается от пластичных материалов. Хрупкие материалы разрушаются без образования шейки. Характеристики каждого материала следует выбирать на основе требований к применению и конструкции.
Характеристики каждого материала следует выбирать на основе требований к применению и конструкции.


