Прямая и обратная пропорциональность. Формулы, обозначение, примеры
Чем старше дерево, тем оно выше. Чем медленнее темп, тем дольше идти до школы. Эти и другие процессы можно описать математическим языком в виде прямой и обратной пропорциональной зависимости. Как это делать — расскажем в этой статье.
Записывайтесь на онлайн-фестиваль для родителей SmartFest!
Ждём вас 8 октября в 13:00. Вместе с педагогами, психологами и другими экспертами в образовании и воспитании ответим на главные вопросы мам и пап.
Бесплатный урок по математике
Записаться
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
Виды зависимостей:
Прямая зависимость. Чем больше одна величина, тем больше вторая. Чем меньше одна величина, тем меньше вторая величина.

Обратная зависимость. Чем больше одна величина, тем меньше вторая. Чем меньше одна величина, тем больше вторая.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
Прямая пропорциональность. Это зависимость, при которой увеличение одного числа ведет к увеличению другого во столько же раз. А уменьшение одного числа ведет к уменьшению другого во столько же раз.
Обратная пропорциональность. Это зависимость, при которой уменьшение одного числа ведет к увеличению другого во столько же раз.
 А увеличение числа наоборот ведет к уменьшению другого во столько же раз.
А увеличение числа наоборот ведет к уменьшению другого во столько же раз.
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
a и d называются крайними членами, b и c — средними.
Основное свойство пропорции
Произведение крайних членов равно произведению средних членов.
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
при постоянной скорости пройденный маршрут прямо-пропорционально зависит от времени;
периметр квадрата и его сторона — прямо-пропорциональные величины;
стоимость конфет, купленных по одной цене, прямо-пропорционально зависит от их количества.
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности y = kx, где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности. |
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Как решаем:
Вспомним формулу для определения пути через скорость и время:
Так как оба автомобиля проделали одинаковый путь, можно составить пропорцию из двух выражений:
Найдем скорость второго автомобиля:
Ответ: 20 км/ч.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней, если они пишут с такой же скоростью?
Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней, если они пишут с такой же скоростью?
Как рассуждаем:
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Составим пропорцию:
14 (постов) / 8 (дней) × х (блогеров) = 420 (постов) / 12 (дней)
Вспомним основное свойство пропорции, согласно которому:
14x × 12 = 420 × 8
х = (420 × 8) / (14 × 12)
х = 20
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины;
при одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи;
количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене.
Формула обратной пропорциональности где y и x — это переменные величины, k — постоянная величина, которую называют коэффициентом обратной пропорциональности. |
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
xy = k.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
Как рассуждаем:
В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.
Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:
Как решаем:
Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию:
30 : 24 = 5 : х
Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:
х = 24 * 5 : 30
х = 4
Значит, 30 человек раскрутят канал за 4 дня.

Ответ: за 4 дня.
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Как рассуждаем:
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Обозначим:
v1 = 75 км/ч
v2 = 52 км/ч
t1 = 13 ч
t2 = х
Как решаем:
Составим пропорцию:
Соотношения равны, но перевернуты относительно друг друга.
Подставим известные значения:
18 ч 45 мин
Ответ: 18 часов 45 минут.
Шпаргалки по математике родителей
Все формулы по математике под рукой
Прямая и обратная пропорциональность. Коэффициент и формулы
- Прямая пропорциональность
- Формула прямой пропорциональности
- Обратная пропорциональность
- Формула обратной пропорциональности
Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.
Пропорциональность величин может быть прямой и обратной.
Прямая пропорциональность
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Рассмотрим пример прямой пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
| Скорость v = 5 км/ч | |||||
|---|---|---|---|---|---|
| Время t (ч) | 1 | 2 | 4 | 8 | 16 |
| Путь s (км) | 5 | 10 | 20 | 40 | 80 |
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s.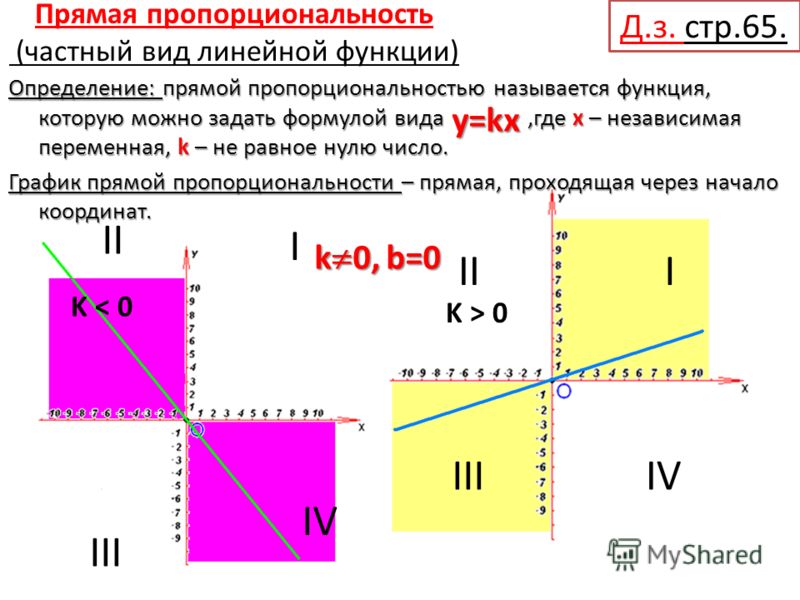 В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
| s | = v, |
| t |
следовательно,
| 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5. |
| 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
| Время t = 2 ч | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 5 | 15 | 45 | 90 |
| Расстояние s (км) | 10 | 30 | 90 | 180 |
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
| s | = t, |
| v |
следовательно,
| 10 | = | 30 | = | 90 | = | 180 | = 2. |
| 5 | 15 | 45 | 90 |
Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
Формула прямой пропорциональности
Формула прямой пропорциональности:
y = kx,
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
| y | = k. |
| x |
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
s = vt,
следовательно,
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Формула обратной пропорциональности
Формула обратной пропорциональности:
| y = | k | , |
| x |
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
xy = k.
Прямая и обратная пропорциональные зависимости / Отношения и пропорции / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Отношения и пропорции
- Прямая и обратная пропорциональные зависимости
Прямая пропорциональная зависимость
| Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз. |
Примеры:
1) — периметр квадрата, — его сторона.
= 4.
Если = 1 см, то = 41 = 4 (см).
Если = 2 см, то = 42 = 8 (см).
Если = 4 см, то = 44 = 16 (см).
Получаем, что каждый раз, увеличивая сторону квадрата в 2 раза, его периметр также будет увеличиваться в 2 раза. Аналогично, если сторону квадрата будем уменьшать в какое-то число раз, то и периметр квадрата будет уменьшаться в это же число раз. Следовательно, величины и прямо пропорциональны. Можно сказать еще и так: «величина прямо пропорциональна величине » или «зависимость между величинами и является прямой пропорциональностью«.
Аналогично, если сторону квадрата будем уменьшать в какое-то число раз, то и периметр квадрата будет уменьшаться в это же число раз. Следовательно, величины и прямо пропорциональны. Можно сказать еще и так: «величина прямо пропорциональна величине » или «зависимость между величинами и является прямой пропорциональностью«.
2) При движении с постоянной скоростью, пройденный путь и время движения прямо пропорциональны, т.к. пройденный путь равен произведению скорости и времени движения.
Пусть скорость движения пешехода 8 км/ч.
Если = 1 ч, то = 81 = 8 (км).
Если = 3 ч, то = 83 = 24 (км).
Если = 9 ч, то = 89 = 72 (км).
Получаем, что каждый раз, увеличивая время в пути в 3 раза, путь также будет увеличиваться в 3 раза, а это и говорит о том, что зависимость между величинами и является прямой пропорциональностью, при условии движения с постоянной скоростью.
Свойство прямо пропорциональных величин:
| Если две величины прямо пропорциональны, то отношение соответствующих значений этих величин равно одному и тому же, постоянному для данных величин, числу. |
В рассмотренных выше примерах для величин и это число равно 4, т.к. : = 4 : 1 = 8 : 2 = 16 : 4 = 4, а для величин и это число равно 8, т.к. : = 8 : 1 = 24 : 3 = 72 : 9 = 8.
Обратная пропорциональная зависимость
| Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз. |
Примеры:
1) Если расстояние является постоянной величиной, то скорость и время движения обратно пропорциональны, т.к. время движения равно частному от деления расстояния на скорость движения.
Пусть расстояние равно 80 км.
Если = 10 км/ч, то = 80 : 10 = 8 (ч).
Если = 20 км/ч, то = 80 : 20 = 4 (ч).
Если = 40 км/ч, то = 80 : 40 = 2 (ч).
Получаем, что каждый раз, увеличивая скорость движения в 2 раза, время движения будет уменьшаться в 2 раза, а это и говорит о том, что зависимость между величинами и является обратной пропорциональностью, при том условии, что расстояние нужно проехать одинаковое.
2) и — стороны прямоугольника, а его площадь 36 см2.
Если = 3 см, то = 36 : 3 = 12 (см).
Если = 6 см, то = 36 : 6 = 6 (см).
Получаем, что величины и обратно пропорциональны, т.к. увеличивая (уменьшая) одну сторону прямоугольника в 2 раза, чтобы его площадь не изменилась, вторую сторону нужно уменьшить (увеличить) в 2 раза.
Свойство обратно пропорциональных величин:
Если две величины обратно пропорциональны, то произведение соответствующих значений этих величин равно одному и тому же для данных величин числу. |
В рассмотренных выше примерах для величин и это число равно 80, т.к. = 108 = 204 = 402 = 80, а для величин и это число равно 12, т.к. = 312 = 66 = 36.
Не всякие величины являются прямо пропорциональными или обратно пропорциональными. Например, размер обуви человека увеличивается при увеличении его возраста, но эти величины не являются пропорциональными, т.к. при удвоении возраста размер обуви человека не удваивается.
Пусть нам дана задача:
Украшение состоит из белого и желтого золота массой 192 г. При этом масса белого золота относится к массе желтого золота как 5 : 7. Надо найти массу белого и желтого золота, из которых сделано украшение.
Решение:
Мы можем считать, что все украшение состоит из 5 + 7 = 12 частей одинаковой массы. По условию масса украшения равна 192 г, а значит, масса одной части украшения равна 192 : 12 = 16 г.
Белое золото соответствует 5 частям, то есть имеет массу 516 = 80 г, а желтое золото соответствует 7 частям, то есть имеет массу 716 = 112 г.
Итак мы получили, что украшение состоит из 80 г белого золота и 112 г желтого золота.
То есть мы число 192 (масса украшения) представить в виде суммы двух слагаемых — 80 и 112, отношение которых равно 5 : 7.
В этом случае говорят, что число 192 разделили в отношении 5 : 7, или по-другому, число 192 представили в виде суммы двух слагаемых, пропорциональных числам 5 и 7.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отношения
Пропорции
Длина окружности и площадь круга
Отношения и пропорции
Правило встречается в следующих упражнениях:
6 класс
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Номер 6, Мерзляк, Полонский, Якир, Учебник
Номер 673, Мерзляк, Полонский, Якир, Учебник
Номер 680, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Задание 786, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 793, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 836, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1495, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 846, Мерзляк, Полонский, Якир, Учебник
Номер 847, Мерзляк, Полонский, Якир, Учебник
6 класс.
 Математика. Прямая и обратная пропорциональные зависимости — Прямая и обратная пропорциональные зависимостиКомментарии преподавателя
Математика. Прямая и обратная пропорциональные зависимости — Прямая и обратная пропорциональные зависимостиКомментарии преподавателяЧастное двух чисел называют отношением этих чисел.
Пропорция – это равенство двух отношений.
Велосипедист за 3 часа проезжает 75 километров. За сколько времени он проедет 150 километров с той же скоростью?
Первым действием найдем скорость велосипедиста. Затем узнаем время, за которое он проедет 150 км.
Из решения видно, что при движении с одной и той же скоростью велосипедист за большее время пройдет большее расстояние. Во сколько раз больше пройденный путь, во столько раз больше затраченное на него время. Такие величины называют прямо пропорциональными.
Определение.
Две величины называют прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Мотоциклист проехал 3 часа со скоростью 60 км/ч. За сколько часов он проедет то же расстояние со скоростью 45 км/ч?
Первым действием найдем длину пройденного пути. Вторым действием – время движения со скоростью 45 км/ч.
Мотоциклист проехал одно и то же расстояние. Во сколько раз скорость мотоциклиста больше, во столько раз меньше затраченное на движение время. Такие величины называют обратно пропорциональными.
Определение.
Две величины называют обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Длина стороны квадрата и периметр связаны прямой пропорциональной зависимостью. Периметр квадрата – это сумма длин четырех его равных сторон. Если длину стороны увеличить в несколько раз, то периметр увеличится во столько же раз.
Длина и ширина прямоугольника (при заданной площади) связаны обратной пропорциональной зависимостью. Площадь прямоугольника – это произведение длины и ширины. Поэтому, чтобы площадь оставалась неизменной при увеличении длины в несколько раз, надо ширину уменьшить во столько же раз.
Площадь прямоугольника – это произведение длины и ширины. Поэтому, чтобы площадь оставалась неизменной при увеличении длины в несколько раз, надо ширину уменьшить во столько же раз.
Скорость автомобиля и путь, который он проедет за определенное время, связаны прямой пропорциональной зависимостью. Время в данном случае – величина постоянная, поэтому при большей скорости автомобиль пройдет больший путь.
Возраст дерева и его высота не связаны пропорциональной зависимостью. В этом случае зависимость между величинами есть. Действительно, высота дерева с возрастом увеличивается, но не во столько же раз.
Стоимость товара, купленного по одной цене, и его количество связаны прямой пропорциональной зависимостью. Чем большее количество товара купили, тем большее количество денег на него потратили.
Возраст человека и размер его обуви не связаны пропорциональной зависимостью. Зависимость между величинами есть. Размер обуви с возрастом увеличивается, но не во столько же раз.
Зависимость между величинами есть. Размер обуви с возрастом увеличивается, но не во столько же раз.
Дробь и ее знаменатель (при постоянном числителе) связаны обратной пропорциональной зависимостью. Чем больше знаменатель, тем меньше дробь при постоянном числителе.
Дробь и ее числитель (если знаменатель не изменяется) связаны прямой пропорциональной зависимостью.
Весной при проведении работ по озеленению города на улице посадили липы. Принялось 95% всех посаженных лип. Сколько посадили лип, если принялось 57 лип?
Величины, о которых говорится в задаче, связаны прямой пропорциональной зависимостью. Составим краткое условие задачи, запишем пропорцию и решим ее.
Стрелки в краткой записи направлены в одну сторону. Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то и вторая тоже возрастает (стрелка тоже вверх).
Для отопления здания школы заготовили угля на 180 дней при норме расхода 0,6 т в день. На сколько дней хватит запаса, если расход ежедневно составит 0,5 т?
Стрелки в краткой записи направлены в разные стороны. . Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то вторая убывает (стрелка вниз). Для каждого столбика таблицы составим отношение верхнего элемента к нижнему, т. к. стрелки направлены в разные стороны, одно из отношений переворачиваем и приравниваем то, что получилось.
Эту задачу и аналогичные ей можно решить, и не выписывая пропорцию в явном виде.
В железной руде на 7 частей железа приходится 3 части примесей. Сколько тонн примесей в руде, которая содержит 73,5 т железа?
Стрелки в краткой записи направлены в одну сторону. Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то и вторая тоже возрастает (стрелка тоже вверх). Для каждого столбика таблицы составим отношение верхнего элемента к нижнему, т. к. стрелки направлены в одну сторону, приравниваем полученные отношения. Составляем пропорцию. Решаем ее. Итак, ответ – 31,5 кг примесей.
Для каждого столбика таблицы составим отношение верхнего элемента к нижнему, т. к. стрелки направлены в одну сторону, приравниваем полученные отношения. Составляем пропорцию. Решаем ее. Итак, ответ – 31,5 кг примесей.
Если две величины прямо пропорциональны, то отношение соответствующих значений этих величин равны. Если две величины обратно пропорциональны, то их произведение постоянно и не равно нулю
Принтер распечатывает 27 страниц за 4,5 минуты. За какое время он распечатает 300 страниц?
Зависимость между количеством напечатанных страниц и временем прямо пропорциональная. Составим пропорцию и решим ее.
Автомобиль проехал 310 километров, истратив 25 литров бензина. Какое расстояние может проехать автомобиль с полным баком, вмещающим 40 литров бензина?
Чем большее расстояние проедет автомобиль, тем больше бензина он потратит. Соответственно, зависимость между величинами прямо пропорциональная.
Соответственно, зависимость между величинами прямо пропорциональная.
Пятнадцать рабочих выполняют заказ за 4 дня. Сколько нужно рабочих, чтобы выполнить тот же заказ за 3 дня?
Для того чтобы выполнить заказ быстрее, количество рабочих нужно увеличить. Соответственно, зависимость обратно пропорциональная.
источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/otnosheniya-i-proporcii/pryamaya-i-obratnaya-proportsionalnye-zavisimosti
источник видео — http://www.youtube.com/watch?v=ALSAtOueOSw
источник видео — http://www.youtube.com/watch?v=buKHM8w_l4M
источник видео — http://www.youtube.com/watch?v=FtTrBSJz0AY
источник видео — http://www.youtube.com/watch?v=YMuRx7h3Mus
источник видео — http://www.youtube.com/watch?v=6ADjiJrSAtQ
источник презентации — http://ppt4web.ru/matematika/prjamaja-i-obratnaja-proporcionalnye-zavisimosti.html
Бобкова С.
 Н. Прямая и обратная пропорциональные зависимости
Н. Прямая и обратная пропорциональные зависимостиАвтор: edu1
Методическая копилка — Математика
МБОУ «Букреевская основная общеобразовательная школа»
Рабочие материалы выступления
на школьном этапе конкурса
«Учитель года 2013»
План — конспект открытого урока
математики в 6 классе по теме:
«Прямая и обратная
пропорциональные зависимости»
учитель математики Бобкова С. Н.
Букреевка, 2013 г.
Цель урока:
Образовательная:Закрепить понятия: пропорция, основное свойство пропорции, прямо пропорциональные величины, обратно пропорциональные величины. Закрепить умение решать задачи с помощью пропорции, познакомить с золотым сечением.
Продолжить формирование обще-учебных умений и навыков:
— планирование ответа;
— навыки самоконтроля;
— устный счет.
Контроль степени усвоения основных знаний, умений и навыков по данной теме.
Развивающая: Развитие умений в применении знаний в конкретной ситуации.
Развитие логического мышления, умения выделять главное, проводить обобщение, делать верные логические выводы.
Развитие умений сравнивать, правильно формулировать задачи и излагать мысли.
Развитие самостоятельной деятельности учащихся.
Воспитательная: Формирование научного мировоззрения, интереса к предмету через содержание учебного материала.
Воспитание умения работать в коллективе, культуры общения, взаимопомощи.
Воспитание таких качеств характера как настойчивость в достижении цели, умение не растеряться в проблемных ситуациях.
Оборудование: карточки с заданиями для самостоятельной работы, презентация.
Ход урока:
1. Устная работа.
1. Что такое пропорция?
2. Как называются числа х и у в пропорции х : а = b : у?
3. Как называются числа т и п в пропорции а: т = n: b?
4. Сформулируйте основное свойство пропорции?
Сформулируйте основное свойство пропорции?
5. Какие ещё свойства пропорции вы знаете?
6. Какие величины называются прямо пропорциональными?
7. Какие величины называются обратно пропорциональными?
1) Верна ли пропорция:
а) 2 : 5 = 16 : 40; б) 7 : 2,1 = 2 : 0,6; в) 4 : 12 = 14 : 4,2
2) Какие числа надо вставить в «окошки», чтобы получить верную пропорцию
а) 33 : 6= : 2; б) 45 : = 15 : 3; в) : = 24 : 6; г) : = : 5.
3) Составьте верную пропорцию из чисел 10, 12, 6 и 5.
4) Повторим алгоритм решения задач на прямую
и обратную пропорциональные зависимости:
• неизвестное число обозначить буквой х
• записать условие задачи
• установить вид зависимости между величинами
• прямую пропорциональную зависимость
обозначить одинаково направленными
стрелками, а обратную пропорциональную
зависимость – противоположно направленными
стрелками.
• записать пропорцию
• найти её неизвестный член.
3. Проверка домашнего задания. Защита творческих работ (домашнее задание было составить задачу на прямую или обратно пропорциональные зависимости)
4. Решение задач
1. За 4м ткани заплатили 180р. Сколько стоят 14м этой ткани? (630 р)
2. Чтобы покрасить стены дома за 2 дня, требуется 20 маляров. За сколько дней эту работу выполнят 4 маляра? ( 10дн)
3. Пассажирский поезд, скорость которого 45км/ч, затратил на некоторый участок пути 4ч. За сколько часов пройдёт этот же участок пути товарный поезд, если его скорость 40 км/ч? ( 4,5 ч)
4. Для изготовления 18 одинаковых приборов потребовалось 27г платины. Сколько платины потребуется для изготовления28 таких приборов? ( 42г или 0,042кг)
5. В 1 кг морской воды содержится 40г соли. Сколько соли содержится в 650 г морской воды? (0,026кг)
5. Самостоятельная работа.
Составить пропорции для решения задач
I- вариант II- вариант
в) и г) а) и б)
а) На пошив 9 рубашек ушло 18,9 м ткани. Сколько метров уйдёт на пошив 12 таких рубашек?
Сколько метров уйдёт на пошив 12 таких рубашек?
б) 6 одинаковых труб заполняют бассейн за 24 минуты. За сколько минут заполнят бассейн 9 таких труб?
в) Бригада из 8 рабочих выполняет задание за 12 дней. Сколько рабочих сможет выполнить это задание за 8 дней, работая с той же производительностью?
г) Из 9,6 кг помидоров получают 4 л томатного соуса. Сколько литров соуса можно получить из 84 кг помидоров?
6. Знакомство с «Золотым сечением» (Демонстрация презентации).
Откройте учебник на странице 144, прочитайте исторический материал.
Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния.
Известно, что еще в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения.
Отношения частей человеческого тела связывались с формулой золотого сечения.
— Пропорции «золотого сечения» создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях.
Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении «золотого сечения».
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника (Прослушивание фрагмент оперы П. И. Чайковского).
И. Чайковского).
7. Рефлексия.
8. Домашнее задание: Самостоятельная работа (другой вариант)
Онлайн урок: Прямая и обратная пропорциональные зависимости по предмету Математика 6 класс
- Урок 23.Прямая и обратная пропорциональные зависимости
На этом уроке мы рассмотрим, что такое прямая и обратная пропорциональные зависимости, научимся оформлять и решать задачи с помощью пропорции, устанавливая пропорциональную зависимость между величинами в ней, рассмотрим примеры задач на прямую и обратную пропорциональную зависимость.
Давайте сначала разберемся, что такое пропорциональность.
Пропорциональность — это зависимость двух величин друг от друга таким образом, что значение отношения этих величин остается постоянным.
Зависимость величин друг от друга может быть прямой и обратной.
Отношение между величинами описываются прямой или обратной пропорциональностью.
Прямая пропорциональность выражается так: \(\mathbf{y = kx}\)
Обратная пропорциональность выражается так: \(\mathbf{y = \frac{k}{x}}\)
где k — это число, которое называют коэффициентом пропорциональности.
x и y величины, зависящие друг от друга.
Пример
Площадь прямоугольника равна \(\mathbf{S = a \cdot b}\), где S— это площадь прямоугольника, а — длина прямоугольника, b — ширина прямоугольника.
Если один из множителей произведения — постоянная величина, то произведение прямо пропорционально второму множителю.
Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.
По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.
Какова эта зависимость, сейчас и рассмотрим.
\(\mathbf{S = a \cdot b}\)
Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.
Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.
\(\mathbf{a = \frac {S}{b}}\) или \(\mathbf{b = \frac {S}{a}}\)
Пусть одна клетка равна 1 см. Рассмотрим рисунок:
Ширина прямоугольника b постоянная величина
b = 4 см
a1 = 6 см
Увеличим ширину прямоугольника — сторону a1 на 1 см, получим
a2 = 7 см
Найдем площади прямоугольников S1 и S2
\(\mathbf{S_{1} = a_{1} \cdot b = 6 \cdot 4 = 24}\) см2
\(\mathbf{S_{2} = a_{2} \cdot b = 7 \cdot 4 = 28}\) см2
Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.
Рассмотрим другой вариант зависимости
Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см
Площадь прямоугольника S постоянная величина
S = 24 см2
b1 = 4 см
\(\mathbf{a_{1} = \frac{S}{b_{1}} = 6}\) (см)
Увеличим высоту прямоугольника- сторону прямоугольника b1 на 2 см, получим
b2 = 6 см
Найдем ширину прямоугольника- сторону a2
\(\mathbf{a_{2} = \frac{S}{b_{2}} = 4}\) (см)
Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.
Таким образом, мы подошли к основным понятиям пропорциональной зависимости.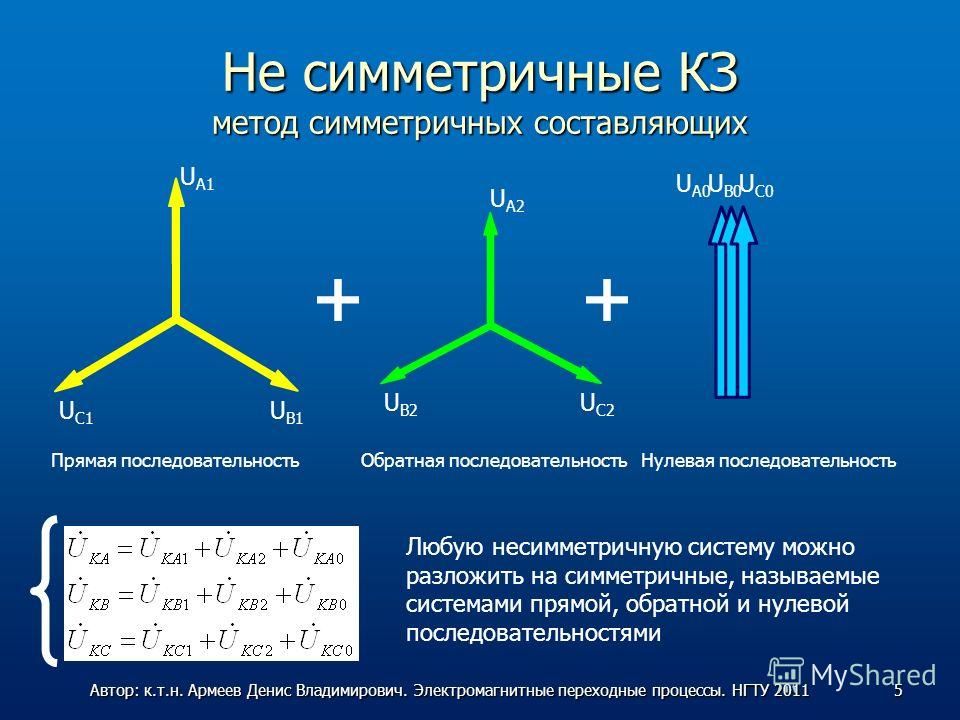 Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:
Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:
Итак:
1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.
2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.
Примеров прямой и обратной пропорциональности множество.
Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.
Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.
Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается
Пройти тест
Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации
Вход Регистрация
Алгоритм решения задач на пропорциональную зависимость состоит из нескольких основных пунктов:
- Обозначить буквой значение неизвестной величины (чаще всего для этого выбирают латинскую букву Х)
- Проанализировать задачу и кратко записать ее условия (краткую запись можно делать в виде таблицы или изображать в виде логической схемы)
- Установить зависимость между величинами
- В краткой записи задачи обозначить стрелками пропорциональную зависимость
— Стрелки, которые направлены в одну сторону, обозначают прямую пропорциональную зависимость величин
— Стрелки, которые направлены в разные стороны, обозначают обратную пропорциональную зависимость величин.
5. Записать пропорцию, учитывая характер пропорциональности величин
6. Составить уравнение
7. Найти неизвестный член уравнения (искомую величину)
8. Записать ответ задачи
Важно помнить, что при составлении краткой записи задачи величины с одинаковыми единицами измерения записывают друг под другом.
Если между величинами прямая пропорциональная зависимость, то пропорция составляется точно в соответствии с краткой записью задачи.
Если между величинами обратная пропорциональная зависимость, то при составлении пропорции одноименные величины меняются местами в одном любом из столбцов таблицы (логической схемы) краткой записи задачи.
Другими словами, при прямо пропорциональной зависимости отношение значений одной величины равно отношению соответствующих значений другой величины.
При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.
Пройти тест
Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации
Вход Регистрация
Рассмотрим некоторые варианты задач на пропорциональную зависимость, в которых величины зависят прямо пропорционально одна от другой.
Задача 1
Для приготовления из 3 кг черной смородины по рецепту требуется 3,3 кг сахара.
Сколько сахара потребуется для приготовления варенья из 5 кг черной смородины?
Решение:
Пусть х (кг) сахара потребуется для приготовления варенья из 5 кг ягод.
Составим краткую запись задачи в виде таблицы:
Определим, как зависят масса сахара и масса ягод.
Чем больше ягод, тем больше нужно сахара, следовательно, между величинами прямо пропорциональная зависимость.
В таблице вертикальными стрелками изображаем прямо пропорциональную зависимость величин.
Так как зависимость величин прямо пропорциональная, составим пропорцию в точном соответствии с таблицей.
Отношение значений одной величины равно отношению соответствующих значений другой величины.
Получим \(\mathbf{\frac{3,3}{x} = \frac{3}{5}}\)
Составим уравнение, используя основное свойство пропорции:
\(\mathbf{{3}\cdot{x} = {5}\cdot{3,3}}\)
\(\mathbf{ {x} = {(5}\cdot{3,3)}\div{3}}\)
\(\mathbf{ {x} = {5,5}}\) (кг) сахара потребуется для приготовления варенья из 5 кг ягод.
Ответ: \(\mathbf{ {x} = {5,5}}\) (кг)
Задача 2
Автомобиль, двигаясь с постоянной скоростью, проехал 400 км за 5 часов.
За какое время автомобиль проедет 600 км?
Решение:
Пусть х (ч) – время, за которое автомобиль проедет 600 км.
Составим краткую запись задачи в виде таблицы:
Определим, как зависят величины S от t, где S — это путь, а t — это время.
Так как движение происходит с постоянной скоростью, то \(\mathbf{ {S} = {V}\cdot{t}}\).
Чем больше расстояние, тем больше требуется времени для преодоления этого расстояния, значит, зависимость между величинами S и t прямо пропорциональная.
Изображаем в таблице краткой записи задачи вертикальными стрелками прямо пропорциональную зависимость величин.
Так как зависимость величин прямо пропорциональная, составим пропорцию в точном соответствии с таблицей.
Отношение значений одной величины равно отношению соответствующих значений другой величины.
Получим \(\mathbf{\frac{5}{x} = \frac{400}{600}}\)
Составим уравнение, используя основное свойство пропорции:
\(\mathbf{ {400}\cdot{x} = {5}\cdot{600}}\)
\(\mathbf{ {x} = {(5}\cdot{600)}\div{400}}\)
\(\mathbf{ {x} = {7,5}}\) (ч) время, за которое автомобиль проедет 600 км
Ответ: \(\mathbf{ {x} = {7,5}}\) (ч)
Примеры решения задач, в которых величины зависят обратно пропорционально одна от другой.
Задача 1
Для перевозки гравия потребовалось 42 машины грузоподъемностью 5 т.
Сколько нужно машин грузоподъемностью 7 т, чтобы перевезти тот же объем гравия?
Решение:
Пусть х (шт) — это количество машин грузоподъемностью 7 т, необходимых для перевозки груза.
Краткую запись задачи оформим в виде таблицы:
Определим, как зависят величины друг от друга.
Чем больше грузоподъемность машины, тем меньше машин потребуется для перевозки груза.
Получаем обратно пропорциональную зависимость.
Изображаем на краткой записи задачи вертикальными стрелками, направленными в разные стороны, обратно пропорциональную зависимость величин.
При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.
А это значит, что при составлении пропорции одно из отношений получится перевернутым.
Получим \(\mathbf{\frac{42}{x} = \frac{7}{5}}\)
Составим уравнение, используя основное свойство пропорции:
\(\mathbf{ {7}\cdot{x} = {42}\cdot{5}}\)
\(\mathbf{ {x} = {(42}\cdot{5)}\div{7}}\)
\(\mathbf{ {x} = {30}}\) (шт.) машин грузоподъёмностью 7 т понадобится для перевозки гравия.
Ответ: \(\mathbf{ {x} = {30}}\) (шт.)
Задача 2
Велосипедист проехал путь от дачи до дома за час со скоростью 10 км/ч. Сколько понадобится времени велосипедисту на преодоление этого пути со скоростью 20 км/ч?
Решение:
Пусть х (ч) время велосипедиста, если он будет двигаться со скоростью 20 км/ч. Составим краткую запись задачи в виде таблицы:
Определим, как зависят V и t, где V— скорость движения велосипедиста, t— время движения.
Чем больше скорость велосипедиста, тем меньше времени ему потребуется для преодоления пути.
Получаем обратно пропорциональную зависимость величин друг от друга.
Изображаем на краткой записи задачи вертикальными стрелками, направленными в разные стороны, обратно пропорциональную зависимость величин.
При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.
А это значит, при составлении пропорции одно из отношений получаем перевернутым.
Получим \(\mathbf{\frac{x}{1} = \frac{10}{20}}\)
Составим уравнение, используя основное свойство пропорции:
\(\mathbf{ {20}\cdot{x} = {10}\cdot{1}}\)
\(\mathbf{ {x} = {(10}\cdot{1)}\div{20}}\)
\(\mathbf{ {x} = {0,5}}\) (ч) время велосипедиста, если он будет двигаться со скоростью 20 км/ч.
Ответ: \(\mathbf{ {x} = {0,5}}\) (ч)
У меня есть дополнительная информация к этой части урока!
Закрыть
Рассмотрим некоторые, часто встречающиеся, варианты прямой и обратной пропорциональной зависимости величин в решении задач
Примеры задач, в которых величины зависят прямо пропорционально одна от другой. | |
Величины, зависящие друг от друга | Величина постоянная |
Величина дроби и ее числитель | Знаменатель дроби |
Объем выполненной работы и затраченное время | Производительность труда |
Производительность труда и объем выполненной работы | Время работы |
Длина пути и время прохождения этого пути | Скорость движения |
Пройденный путь и скорость движения | Время движения |
Количество товара и стоимость | Цена товара |
Длина (ширина) прямоугольника и его площадь | Ширина (длина) |
Примеры задач, в которых величины зависят обратно пропорционально одна от другой | |
Знаменатель дроби и значение дроби | Числитель дроби |
Число рабочих и время выполнения ими заданной работы | Производительность всех рабочих |
Производительность труда и время потраченное на работу | Объем работы |
Скорость движения и время | Путь |
Количество товара и его цена | Стоимость покупки |
Пройти тест
Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации
Вход Регистрация
Пройти тест
Контроллеры: управление прямого и обратного действия
Действие контроллера дистилляционной колонны
температура колонки постоянна, в то время как уровень в накопителе регулируется путем управления потоком флегмы.
Q: Насколько я понимаю, если выход контроллера увеличивается при увеличении значения измерения, то это регулятор прямого действия, а если выход контроллера уменьшается при увеличении измерения, это регулятор обратного действия. Кроме того, при минимальной мощности контроллера должно быть достигнуто желаемое безотказное действие. Например, если у нас есть два контроллера на дистилляционной колонне — рефлюкс и верхний погон, — где клапан управления обратным потоком открывается при отказе, а регулирующий клапан верхнего погона нетто — закрывается при отказе, контроллер обратного потока будет обратного действия, а чистый Накладной регулятор будет прямого действия. Правильно ли я понимаю? — Васант Варке / [email protected]
A: Положение отказа клапана и действия контроллера определяются независимо, поэтому поговорим о них отдельно.
Положение отказа клапана определяется соображениями безопасности. Если в случае неудачи вы хотите, чтобы ваша колонка работала с полным обратным холодильником, ваш выбор правильный (рис. 1). Предполагая, что приводы клапанов являются пневматическими с пружинным приводом (вы не сказали, какие они были), и предполагая, что вы определяете «отказ» как прекращение подачи воздуха, пружина будет действовать, открывая клапан с отказоустойчивым открытием (FO). и закрывать клапан с аварийным закрытием (FC), независимо от действий контроллера. (Я не упоминаю о роли позиционеров, потому что мне не нравится использовать их на клапанах управления потоком, потому что они могут быть медленнее, чем процесс потока, и, следовательно, они могут вызвать цикличность.)
1). Предполагая, что приводы клапанов являются пневматическими с пружинным приводом (вы не сказали, какие они были), и предполагая, что вы определяете «отказ» как прекращение подачи воздуха, пружина будет действовать, открывая клапан с отказоустойчивым открытием (FO). и закрывать клапан с аварийным закрытием (FC), независимо от действий контроллера. (Я не упоминаю о роли позиционеров, потому что мне не нравится использовать их на клапанах управления потоком, потому что они могут быть медленнее, чем процесс потока, и, следовательно, они могут вызвать цикличность.)
Теперь обратимся к теме действия контроллера. Если предположить, что ваша система такая, как показано на рисунке, повышение температуры колонки должно привести к усилению охлаждения, что достигается за счет возврата большего количества холодного орошения в колонку. Это означает, что регулятор температуры (ТС) должен уменьшить уставку потока флегмы, что, в свою очередь, повысит уровень в накопителе, и для преодоления этого регулятор уровня (LC) увеличит уставку регулятора потока флегмы (FC). . Таким образом, увеличение измерения требует, чтобы TC уменьшал свой выходной сигнал (обратное действие, R/A), в то время как LC увеличивает свой выходной сигнал при увеличении уровня (D/A). Реакцией подчиненных контроллеров FC является увеличение расхода через их клапаны по мере того, как ведущий повышает свою уставку, поэтому с клапаном FC это будет D/A, а с клапаном FO это будет R/A.
. Таким образом, увеличение измерения требует, чтобы TC уменьшал свой выходной сигнал (обратное действие, R/A), в то время как LC увеличивает свой выходной сигнал при увеличении уровня (D/A). Реакцией подчиненных контроллеров FC является увеличение расхода через их клапаны по мере того, как ведущий повышает свою уставку, поэтому с клапаном FC это будет D/A, а с клапаном FO это будет R/A.
Естественно, система управления, показанная на рисунке, очень проста (ничего не делает для взаимодействий и т. д.), но ее достаточно для объяснения рассматриваемого вопроса.
Бела Липтак
[email protected]
A: Прямое действие означает, что выход контроллера увеличивается, если измерение увеличивается. Косвенное (обратное) действие означает, что выход контроллера падает, когда измерение увеличивается.
Аль Павловски, ЧП
[email protected]
Ответ: Не совсем верно. Действие при отказе регулирующего клапана (а иногда и действие позиционера клапана) также имеет значение. Чтобы убедиться, что у вас есть общая отрицательная обратная связь, вам нужно проследить весь цикл от датчика (увеличение / уменьшение выходного сигнала при увеличении переменной) через контроллер (где вы можете изменить усиление) до позиционера (обычно прямое действие, но глупые люди иногда пытаются скрыть ошибки, меняя выход) на клапан (увеличение положения штока увеличивает или уменьшает измеряемую переменную?).
Чтобы убедиться, что у вас есть общая отрицательная обратная связь, вам нужно проследить весь цикл от датчика (увеличение / уменьшение выходного сигнала при увеличении переменной) через контроллер (где вы можете изменить усиление) до позиционера (обычно прямое действие, но глупые люди иногда пытаются скрыть ошибки, меняя выход) на клапан (увеличение положения штока увеличивает или уменьшает измеряемую переменную?).
Ян Х.Гибсон
[email protected]
A: Действие контроллера зависит от определения ошибки. Если ошибка = заданное значение – переменная процесса, то контроллер обратного действия приведет к уменьшению переменной процесса при увеличении выходного сигнала контроллера, и наоборот.
Положение отказа клапана — это не функция контроллера, а функция безопасности или нулевой энергии в случае сбоя подачи энергии на исполнительный элемент управления. РСУ имеют разные способы обработки положения отказа и действия контроллера, и конфигурация должна быть выполнена в соответствии с тем, что имеет смысл для работы.
Сигифредо Нино
[email protected]
A: Обычно мне нравится смотреть на показания ошибки в контроллере, то есть на разницу между уставкой и переменной процесса. Если увеличение ошибки увеличивает выходной сигнал контроллера, это контроллер прямого действия. Если увеличение ошибки приводит к уменьшению выходного сигнала контроллера, это контроллер обратного действия.
Хитен А. Далал, ИП, PMP
[email protected]
A: Вопрос, который я всегда задаю: когда измерение увеличивается, что должен сделать выход контроллера, чтобы вернуть его к заданному значению? Например, если контроллер обратного давления (где регулирующий клапан открывается для уменьшения давления, измеренного перед ним) обнаруживает повышение давления, он должен увеличить свой выходной сигнал. Увеличение измерения/увеличение выходного сигнала является «увеличением/увеличением» или прямым действием.
Напротив, почти все контроллеры потока, которые я видел, имеют «увеличение/уменьшение» или обратное действие. Рефлюксная петля мистера Уорка действовала бы в обратном направлении. Мы хотим, чтобы клапан был «закрыт», когда выход контроллера равен 0 %, и «открыт», когда он равен 100 %, независимо от положения отказа клапана. Это делает его последовательным для оператора. Поэтому, когда контроллер видит увеличение расхода, он должен уменьшить свой выход (закрыть клапан), чтобы вернуть его к заданному значению.
Не думаю, что можно обобщать с точки зрения применения. Несмотря на то, что контур прямого действия встречается редко, вы можете спроектировать его или столкнуться с ним. Если бы мы имели дело строго со старой пневматикой или автономными механическими контроллерами, то ваш пример с рефлюксом был бы «прямого действия». Пневматический контроллер должен был бы увеличить свой сигнал в ответ на увеличение расхода.
Регулятор уровня, выход которого управляет клапаном на входе в бак, имеет обратное действие, но если клапан находится на выходе, он становится прямым. Температурное приложение может контролировать подачу охлаждающей воды к теплообменнику (прямое) или байпас охлаждающей воды (обратное). то это» для прямого или обратного действия. Может я медлительный, но все равно приходится продумывать каждое приложение.
Температурное приложение может контролировать подачу охлаждающей воды к теплообменнику (прямое) или байпас охлаждающей воды (обратное). то это» для прямого или обратного действия. Может я медлительный, но все равно приходится продумывать каждое приложение.
Джон Резабек
[email protected]
A: Я полагаю, что у вас обратная причина и следствие. Думайте только о контроллере. Рассматривайте вход (переменную процесса) контроллера как причину, а выход контроллера как следствие. Если контроллер настроен на прямое действие, то увеличение PV приведет к увеличению выхода. Если контроллер настроен на обратное действие, увеличение PV приведет к уменьшению выходного сигнала.
Чтобы правильно настроить прямое/обратное действие, необходимо учитывать влияние процесса на всем пути от выхода контроллера до переменной процесса. Выход контроллера вызывает открытие или закрытие клапана? Некоторые клапаны открываются при отказе; некоторые закрываются при отказе. Приводит ли увеличение положения клапана к повышению или понижению PV? Открытие парового клапана теплообменника (HX) приведет к повышению температуры на выходе HX, тогда как открытие клапана охлаждающей воды вызовет снижение температуры на выходе HX.
Приводит ли увеличение положения клапана к повышению или понижению PV? Открытие парового клапана теплообменника (HX) приведет к повышению температуры на выходе HX, тогда как открытие клапана охлаждающей воды вызовет снижение температуры на выходе HX.
Таким образом, принимая во внимание все эффекты между выходным сигналом контроллера и PV, если увеличение выходного сигнала контроллера вызывает рост PV, или уменьшение выходного сигнала контроллера вызывает падение PV (т. е. PV движется в том же направлении). направление как выход регулятора), то процесс можно назвать прямодействующим, поэтому регулятор следует настроить на противоположное, обратнодействующее. Таким образом, если нарушение процесса приводит к увеличению PV, регулятор обратного действия уменьшит свой выходной сигнал. Следовательно, это уменьшение выходного сигнала контроллера приведет к уменьшению технологической переменной прямого действия, тем самым сдвинув ее в направлении, противоположном тому, которое вызвало возмущение.
Harold Wade
[email protected]
A: Я считаю, что ваше понимание прямого/обратного действия применительно к регулирующим клапанам правильное. Однако отказоустойчивое действие не имеет ничего общего с прямым/обратным действием. Действие при отказе определяется исключительно положением пружины, против которой действует пневматическая диафрагма в приводе регулирующего клапана. Они определяются независимо при задании регулирующего клапана (отказоустойчивое действие) и снова при настройке позиционера регулирующего клапана или контроллера, выходящего на регулирующий клапан (прямого/обратного действия).
Дик Каро
[email protected]
Что такое прямое и обратное действие?
УП150
Компактный программный регулятор температуры размером 1/16 DIN предлагает один шаблон программы с 16 сегментами. Он также имеет универсальный вход, два выхода событий, автонастройку и функцию подавления перерегулирования «SUPER» в стандартной комплектации.
Узнать больше Выход ретрансляции и связь RS485 являются дополнительными функциями.
Выход ретрансляции и связь RS485 являются дополнительными функциями.Программный контроллер UP350
Программный контроллер UP350
Узнать большеПрограммный контроллер UP351
Программный контроллер UP351
Узнать большеUP550
Усовершенствованный программный контроллер размером 1/4 DIN имеет 5 мощных режимов управления и 30 шаблонов программ. Он поставляется с большим дисплеем PV и ЖК-дисплеем для интерактивной настройки и программирования. Также представлены универсальные входы/выходы «SUPER» и «SUPER2». Также доступны позиционно-пропорциональные модели, модели с обогревом/охлаждением и опция связи RS-485.
Узнать большеUP750
Программный контроллер большой емкости размером 1/4 DIN поддерживает пользовательские вычисления, 300 программных шаблонов и 11 мощных режимов управления, включая двухконтурное управление. Он поставляется с хорошо видимым большим дисплеем PV и ЖК-дисплеем для интерактивной настройки и программирования.
Узнать больше Также представлены универсальные входы/выходы «SUPER» и «SUPER2». Два порта связи RS-485 являются опцией.
Также представлены универсальные входы/выходы «SUPER» и «SUPER2». Два порта связи RS-485 являются опцией.1000 долларов США
Цифровой контроллер-индикатор размером 72×144×100 мм имеет четкий гистограммный дисплей для PV, SV и MV. Он поставляется с 14 мощными режимами управления, включая дополнительные пользовательские вычисления и управление с двойным контуром. Универсальный вход, автонастройка, функции «СУПЕР» входят в стандартную комплектацию. Опционально доступны пропорциональное управление по положению и связь через RS485.
Узнать большеУТ130
Компактный и удобный для просмотра регулятор температуры размером 1/16 DIN с большим (высотой 17,5 мм) 3-разрядным дисплеем. Универсальный вход, функция подавления выброса «SUPER» и динамическая автонастройка входят в стандартную комплектацию. Управление обогревом/охлаждением и связь по RS485 являются дополнительными функциями.
Узнать большеУТ150
Компактный универсальный регулятор температуры общего назначения размером 1/16 DIN имеет универсальный вход, функцию подавления выброса «SUPER» и динамическую автонастройку в стандартной комплектации.
Узнать больше Управление обогревом/охлаждением, выход ретрансляции, функция таймера и связь RS485 являются дополнительными функциями.
Управление обогревом/охлаждением, выход ретрансляции, функция таймера и связь RS485 являются дополнительными функциями.Цифровой индикаторный контроллер UT320
Контроллер цифровой индикации UT320 снят с производства 01.01.2010. Контроллер температуры UT35A/UT32A является сменным продуктом.
Узнать большеЦифровой индикаторный контроллер UT321
Цифровой контроллер индикации UT321 снят с производства 01.01.2010. Контроллер температуры UT35A/UT32A является сменным продуктом.
Узнать большеЦифровой индикаторный контроллер UT350
Контроллер цифровой индикации UT350
Узнать большеЦифровой индикаторный контроллер UT351
Контроллер цифровой индикации UT351
Узнать большеUT420
Название модели: UT420
Узнать большеЦифровой индикаторный контроллер UT450
Контроллер цифровой индикации UT450
Узнать большеЦифровой индикаторный контроллер UT520
Контроллер цифровой индикации UT520 снят с производства 01.
Узнать больше 01.2010. UTAdvanced UT52A является сменным продуктом.
01.2010. UTAdvanced UT52A является сменным продуктом.Цифровой индикаторный контроллер UT550
Контроллер цифровой индикации UT550
Узнать большеUT750
Высокофункциональный контроллер размером 1/4 DIN поставляется с пользовательскими вычислениями и 12 мощными функциями управления, включая двухконтурное управление. Он также оснащен удобным для просмотра большим дисплеем PV и ЖК-дисплеем для интерактивной настройки и программирования. Универсальный ввод/вывод, автонастройка, функции «SUPER» и «SUPER2» входят в стандартную комплектацию. Два порта связи RS-485 являются опцией.
Узнать больше
Реле давления прямого и обратного действия
- Форум
- Общий форум
- Общее обсуждение
- Реле давления прямого и обратного действия
- Согласие на использование файлов cookie
Мы используем файлы cookie, чтобы улучшить работу вашего веб-сайта.
 Чтобы узнать об использовании нами файлов cookie и о том, как вы можете управлять своими настройками файлов cookie, ознакомьтесь с нашей Политикой использования файлов cookie. Продолжая использовать веб-сайт, вы соглашаетесь на использование нами файлов cookie.
Чтобы узнать об использовании нами файлов cookie и о том, как вы можете управлять своими настройками файлов cookie, ознакомьтесь с нашей Политикой использования файлов cookie. Продолжая использовать веб-сайт, вы соглашаетесь на использование нами файлов cookie. - Добро пожаловать на HVAC-Talk.com, сайт, не посвященный DIY, и главный источник информации и знаний в области HVAC для профессионалов отрасли! Здесь вы можете присоединиться к более чем 150 000 профессионалов и энтузиастов ОВКВ со всего мира, которые обсуждают все, что связано с ОВКВ/Х. В настоящее время вы просматриваете как НЕЗАРЕГИСТРИРОВАННЫЙ гость, что дает вам ограниченный доступ к просмотру обсуждений
Чтобы получить полный доступ к нашим форумам, вы должны зарегистрироваться; за бесплатно 9счет 0244. Как зарегистрированный гость вы сможете:
- Участвуйте в более чем 40 различных форумах и ищите/просматривайте почти 3 миллиона сообщений.
- Размещайте фотографии, отвечайте на опросы и получайте доступ к другим специальным функциям
- Получите доступ к нашему бесплатному разделу AOP (Спросите профессионала), чтобы получить реальные ответы на свои вопросы.

Мы не рекомендуем регистрироваться с использованием адреса электронной почты AT&T, BellSouth, AOL или Yahoo. Если у вас возникли проблемы с регистрацией или входом в аккаунт, обратитесь в службу поддержки.
13 апреля 2010 г., 17:58 #1
Мне сказали, что реле низкого давления газа имеют обратное действие в том смысле, что они размыкаются, если давление газа падает ниже уставки регулятора давления прибора, а реле высокого давления газа имеют прямое действие, поскольку они размыкаются, когда давление газа превышает выходное давление редуктора.
 регулятор давления прибора.
регулятор давления прибора.Мой вопрос заключается в том, как определить Обратное и Прямое действие, поскольку они относятся к приведенному выше объяснению?
Большое спасибо за любую помощь в этом.
Джастин
Ответить с цитатой
13 апреля 2010 г., 19:42 #2
Первоначально написал Justinw
Мне сказали, что реле низкого давления газа имеют обратное действие, поскольку они размыкаются, если давление газа падает ниже заданного значения регулятора давления прибора, и что реле высокого давления газа имеют прямое действие, поскольку они размыкаются.
 когда давление газа превышает выходное давление регулятора давления прибора.
когда давление газа превышает выходное давление регулятора давления прибора.Мой вопрос заключается в том, как определить Обратное и Прямое действие, поскольку они относятся к приведенному выше объяснению?
Большое спасибо за любую помощь.
Джастин
Забавно Я бы сказал наоборот.Выключатель обратного действия разрывает цепь при повышении давления. Реле прямого действия замыкает цепь при повышении давления.
Меня всегда учили, что если выход увеличивается с повышением входа, то это прямое действие. Таким образом, реле низкого давления …… увеличивает напряжение (замыкает контакты) с увеличением давления газа.
Ответить с цитатой
13 апреля 2010 г., 19:56 #3
Первоначально Послано ascj
Забавно я бы сказал наоборот.

Выключатель обратного действия разрывает цепь при повышении давления. Реле прямого действия замыкает цепь при повышении давления.
Меня всегда учили, что если выход увеличивается с повышением входа, то это прямое действие. Таким образом, реле низкого давления …… увеличивает напряжение (замыкает контакты) с увеличением давления газа.
Поправьте меня, если я ошибаюсь, но ни прямого, ни обратного действия нет….. обратное или прямое действие относится к выходному сигналу, который изменяется в зависимости от входного сигнала (т.е. пневматического или DDC-термостата). классифицируются как открытые или закрытые при повышении или понижении входного сигнала (в данном случае давления газа).Ответить с цитатой
13 апреля 2010 г., 20:02 #4
Первоначально написал C-Jac486
Поправьте меня, если я ошибаюсь, но ни прямое, ни обратное действие.
низкий выход? …. обратное или прямое действие относится к выходному сигналу, который изменяется из-за входного сигнала (т.е. пневматический или DDC-термостат.) Переключатели будут просто классифицироваться как разомкнутые или замкнутые в зависимости от повышения или понижения входного сигнала (в данном случае давления газа).
…. обратное или прямое действие относится к выходному сигналу, который изменяется из-за входного сигнала (т.е. пневматический или DDC-термостат.) Переключатели будут просто классифицироваться как разомкнутые или замкнутые в зависимости от повышения или понижения входного сигнала (в данном случае давления газа).Я согласен, что 99% выходных сигналов прямого или обратного действия основаны на модулирующем токе или напряжении.
Ответить с цитатой
13 апреля 2010 г., 20:47 #5
Первоначально написал C-Jac486
Поправьте меня, если я ошибаюсь, но ни прямое, ни обратное действие.
Я думаю, что у вас есть лучший ответ. …. обратное или прямое действие относится к выходному сигналу, который изменяется из-за входного сигнала (т.е. пневматический или DDC-термостат.) Переключатели будут просто классифицироваться как открытые или закрытые в зависимости от подъема или падения входного сигнала (в данном случае давления газа).
…. обратное или прямое действие относится к выходному сигналу, который изменяется из-за входного сигнала (т.е. пневматический или DDC-термостат.) Переключатели будут просто классифицироваться как открытые или закрытые в зависимости от подъема или падения входного сигнала (в данном случае давления газа).Ответить с цитатой
13 апреля 2010 г., 20:56 #6
Первоначально Послано ascj
Но разве закрытый переключатель не будет высоким выходом, а открытый переключатель будет низким выходом?
Я согласен с тем, что 99% выходных сигналов прямого или обратного действия основаны на модулирующем токе или напряжении.
Я понимаю, что вы имеете в виду, и технически вы можете классифицировать переключатель как обратного или прямого действия…. но я не собираюсь заниматься обратным или прямым, а скорее размыканием или замыканием на подъеме или понижении.
Ответить с цитатой
« Предыдущая тема | Следующая тема »
Разрешения на публикацию
Разработка количественной ПЦР с прямой обратной транскрипцией (dirRT-qPCR) для клинической диагностики вируса Зика
. 2019 авг; 85: 167-174.
дои: 10.1016/j.ijid.2019.06.007. Epub 2019 13 июня.
Лан Ли 1 , Цзянь-Ан Хэ 2 , Вэй Ван 3 , Юнь Ся 2 , Ли Сун 1 , Зе-Хан Чен 4 , Хан-Чжи Цзо 4 , Сюань-Пин Тан 5 , Аарон Хо-Пуи Хо 6 , Сиу-Кай Конг 7 , Джеки Фонг-Чуэн Лу 8 , Хуа-Вэнь Ли 9 , Дайонг Гу 10
Принадлежности
- 1 Школа общественного здравоохранения, Вторая школа клинической медицины, Гуандунский медицинский университет, Дунгуань, 523808, КНР; Шэньчжэньский международный медицинский центр для путешественников и Шэньчжэньская академия инспекции и карантина, Шэньчжэньский таможенный округ, Шэньчжэнь, 518033, КНР.

- 2 Шэньчжэньский международный медицинский центр для путешественников и Шэньчжэньская академия инспекции и карантина, Шэньчжэньский таможенный округ, Шэньчжэнь, 518033, КНР.
- 3 Отделение лабораторной медицины, Вторая народная больница Шэньчжэня, Первая дочерняя больница Шэньчжэньского университета, Центр медицинских наук, Шэньчжэнь, 518035, КНР.
- 4 Школа общественного здравоохранения, Вторая школа клинической медицины, Гуандунский медицинский университет, Дунгуань, 523808, КНР.
- 5 Shenzhen gene-one Biotechnology Co., Ltd., 518000, КНР.
- 6 Кафедра биомедицинской инженерии Китайского университета Гонконга, САР Гонконг, КНР.

- 7 Программа биохимии, Школа наук о жизни, Китайский университет Гонконга, САР Гонконг, КНР.
- 8 Кафедра биомедицинской инженерии Китайского университета Гонконга, САР Гонконг, КНР; Программа биохимии, Школа наук о жизни, Китайский университет Гонконга, САР Гонконг, КНР. Электронный адрес: [email protected].
- 9 Школа общественного здравоохранения, Вторая школа клинической медицины, Гуандунский медицинский университет, Дунгуань, 523808, КНР. Электронный адрес: [email protected].
- 10 Шэньчжэньский международный медицинский центр для путешественников и Шэньчжэньская академия инспекции и карантина, Шэньчжэньский таможенный округ, Шэньчжэнь, 518033, КНР; Отделение лабораторной медицины, Вторая народная больница Шэньчжэня, Первая дочерняя больница Шэньчжэньского университета, Центр медицинских наук, Шэньчжэнь, 518035, КНР.
 Электронный адрес: [email protected].
Электронный адрес: [email protected].
- PMID: 31202908
- DOI: 10.1016/j.ijid.2019.06.007
Бесплатная статья
Ланг Ли и др. Int J Infect Dis. 2019 авг.
Бесплатная статья
. 2019 авг; 85: 167-174.
doi: 10.1016/j.ijid.2019.06.007. Epub 2019 13 июня.
Авторы
Лан Ли 1 , Цзянь-Ан Хэ 2 , Вэй Ван 3 , Юнь Ся 2 , Ли Сун 1 , Зе-Хан Чен 4 , Хан-Чжи Цзо 4 , Сюань-Пин Тан 5 , Аарон Хо-Пуи Хо 6 , Сиу-Кай Конг 7 , Джеки Фонг-Чуэн Лу 8 , Хуа-Вэнь Ли 9 , Дайонг Гу 10
Принадлежности
- 1 Школа общественного здравоохранения, Вторая школа клинической медицины, Гуандунский медицинский университет, Дунгуань, 523808, КНР; Шэньчжэньский международный медицинский центр для путешественников и Шэньчжэньская академия инспекции и карантина, Шэньчжэньский таможенный округ, Шэньчжэнь, 518033, КНР.

- 2 Шэньчжэньский международный медицинский центр для путешественников и Шэньчжэньская академия инспекции и карантина, Шэньчжэньский таможенный округ, Шэньчжэнь, 518033, КНР.
- 3 Отделение лабораторной медицины, Вторая народная больница Шэньчжэня, Первая дочерняя больница Шэньчжэньского университета, Центр медицинских наук, Шэньчжэнь, 518035, КНР.
- 4 Школа общественного здравоохранения, Вторая школа клинической медицины, Гуандунский медицинский университет, Дунгуань, 523808, КНР.
- 5 Shenzhen gene-one Biotechnology Co., Ltd., 518000, КНР.
- 6 Кафедра биомедицинской инженерии Китайского университета Гонконга, САР Гонконг, КНР.

- 7 Программа биохимии, Школа наук о жизни, Китайский университет Гонконга, САР Гонконг, КНР.
- 8 Кафедра биомедицинской инженерии Китайского университета Гонконга, САР Гонконг, КНР; Программа биохимии, Школа наук о жизни, Китайский университет Гонконга, САР Гонконг, КНР. Электронный адрес: [email protected].
- 9 Школа общественного здравоохранения, Вторая школа клинической медицины, Гуандунский медицинский университет, Дунгуань, 523808, КНР. Электронный адрес: [email protected].
- 10 Шэньчжэньский международный медицинский центр для путешественников и Шэньчжэньская академия инспекции и карантина, Шэньчжэньский таможенный округ, Шэньчжэнь, 518033, КНР; Отделение лабораторной медицины, Вторая народная больница Шэньчжэня, Первая дочерняя больница Шэньчжэньского университета, Центр медицинских наук, Шэньчжэнь, 518035, КНР.
 Электронный адрес: [email protected].
Электронный адрес: [email protected].
- PMID: 31202908
- DOI: 10.1016/j.ijid.2019.06.007
Абстрактный
Задача: Анализ полимеразной цепной реакции (ПЦР) на основе нуклеиновых кислот обычно применяется для выявления заражения вирусом Зика (ZIKV). Однако длительная и трудоемкая предварительная обработка образцов, необходимая для удаления ингибиторов, вызывающих ложноотрицательные результаты в клинических образцах, нецелесообразна для использования в областях с ограниченными ресурсами. Цель состояла в том, чтобы разработать прямой количественный ПЦР с обратной транскрипцией (dirRT-qPCR) для диагностики ZIKV непосредственно из клинических образцов.
Методы: Комбинация устойчивых к ингибиторам полимераз, энхансеров полимеразы и условий dirRT-qPCR была оптимизирована для различных клинических образцов, включая кровь и сыворотку. Чувствительность оценивали с добавлением стандартной ДНК в смоделированные образцы. Специфичность оценивали с использованием клинических образцов других инфекций, таких как вирус денге и вирус чикунгунья.
Полученные результаты: Были достигнуты высокая специфичность и чувствительность, а предел обнаружения (LOD) анализа составил 9,5×10 1 копий РНК ZIKV/реакция. Для клинической диагностики ZIKV на месте требовался образец объемом 5 мкл, и диагностика могла быть завершена в течение 2 часов.
Выводы: Этот надежный анализ dirRT-qPCR показывает высокий потенциал для диагностики по месту оказания медицинской помощи, а комбинации праймер-зонд также могут быть расширены для обнаружения других вирусов. Он реализует цель крупномасштабного скрининга вирусных инфекций на местах и может использоваться для ранней диагностики, предотвращения и контроля вирусных вспышек.
Он реализует цель крупномасштабного скрининга вирусных инфекций на местах и может использоваться для ранней диагностики, предотвращения и контроля вирусных вспышек.
Ключевые слова: Клиническая диагностика Зика; Прямое обнаружение образца; Молекулярная диагностика; dirRT-КПЦР.
Copyright © 2019 Автор(ы). Опубликовано Elsevier Ltd. Все права защищены.
Похожие статьи
Оценка применяемой в полевых условиях изотермической ПЦР с изолированной обратной транскрипцией для быстрого и чувствительного обнаружения вируса Зика на месте.
Carossino M, Li Y, Lee PA, Tsai CF, Chou PH, Williams D, Skillman A, Frank Cook R, Brown G, Chang HG, Wang HT, Balasuriya UBR. Кароссино М. и др. BMC Infect Dis. 2017 19 декабря; 17 (1): 778. doi: 10.1186/s12879-017-2852-4.
 BMC Infect Dis. 2017.
PMID: 29258444
Бесплатная статья ЧВК.
BMC Infect Dis. 2017.
PMID: 29258444
Бесплатная статья ЧВК.Улучшенное обнаружение РНК вируса Зика в образцах человека и животных с помощью нового, высокочувствительного и специфичного анализа ОТ-ПЦР в реальном времени, нацеленного на 5′-нетранслируемую область вируса Зика.
Чан Дж.Ф., Ип К.С., Ти К.М., Чжу З., Цанг Дж.О., Чик К.К., Цанг Т.Г., Чан К.С., Пун В.К., Сридхар С., Инь Ф., Хунг И.Ф., Чау С.К., Чжан А.Дж., Чан К.Х., Юэн К.И. Чан Дж. Ф. и соавт. Троп Мед Int Health. 2017 май; 22(5):594-603. doi: 10.1111/tmi.12857. Epub 2017 16 марта. Троп Мед Int Health. 2017. PMID: 28214373
Оптимизация ПЦР-обнаружения вируса Зика в различных биологических жидкостях.
Горчаков Р., Берри Р. М., Патель С. М.
 , Эль Сахли Х. М., Ронка С. Е., Мюррей К. О.
Горчаков Р. и соавт.
Am J Trop Med Hyg. 2019Февраль; 100 (2): 427-433. doi: 10.4269/ajtmh.18-0755.
Am J Trop Med Hyg. 2019.
PMID: 30560770
Бесплатная статья ЧВК.
, Эль Сахли Х. М., Ронка С. Е., Мюррей К. О.
Горчаков Р. и соавт.
Am J Trop Med Hyg. 2019Февраль; 100 (2): 427-433. doi: 10.4269/ajtmh.18-0755.
Am J Trop Med Hyg. 2019.
PMID: 30560770
Бесплатная статья ЧВК.Петлевая изотермическая амплификация (LAMP) для диагностики вируса Зика: обзор.
Сильва SJRD, Парди К., Пена Л. Сильва SJRD и др. Вирусы. 2019 23 декабря; 12(1):19. дои: 10.3390/v12010019. Вирусы. 2019. PMID: 31877989 Бесплатная статья ЧВК. Обзор.
Вирус Зика.
Муссо Д., Гублер Д.Дж. Муссо Д. и др. Clin Microbiol Rev. 2016 Jul; 29(3):487-524. doi: 10.1128/CMR.00072-15. Клин Микробиол Ред. 2016. PMID: 27029595 Бесплатная статья ЧВК. Обзор.
Посмотреть все похожие статьи
Цитируется
Последние молекулярные методы диагностики инфекций Зика и Чикунгунья: систематический обзор.

Cardona-Trujillo MC, Ocampo-Cárdenas T, Tabares-Villa FA, Zuluaga-Vélez A, Sepulveda-Arias JC. Cardona-Trujillo MC, et al. Гелион. 2022, 13 августа; 8(8):e10225. doi: 10.1016/j.heliyon.2022.e10225. Электронная коллекция 2022 авг. Гелион. 2022. PMID: 36033321 Бесплатная статья ЧВК.
ПЦР с прямой обратной транскрипцией в реальном времени вирусной РНК из образцов слюны с использованием микрочастиц гидрогеля.
Кифаро Э.Г., Ким М.Дж., Юнг С., Но Ч.Ю., Сонг С.С., Мисинзо Г., Ким С.К. Кифаро Э.Г. и соавт. Биочип Дж. 2022 авг. 8:1-13. doi: 10.1007/s13206-022-00065-0. Онлайн перед печатью. Биочип Дж. 2022. PMID: 35968254 Бесплатная статья ЧВК.
Эффект матрицы в RT-PCR обнаружении SARS-CoV-2 с использованием слюны без выделения РНК.

Мораис О., Алвес М.Р., Рамос С., Феррейра Ф., Фернандеш П. Мораис О. и др. Диагностика (Базель). 2022 25 июня; 12 (7): 1547. дои: 10.3390/диагностика12071547. Диагностика (Базель). 2022. PMID: 35885453 Бесплатная статья ЧВК.
Смартфон с клипсой и микрофлюидный процессор для быстрого обнаружения вируса Зика в цельной крови от образца до ответа с использованием пространственной RT-LAMP.
Jankelow AM, Lee H, Wang W, Hoang TH, Bacon A, Sun F, Chae S, Kindratenko V, Koprowski K, Stavins RA, Ceriani DD, Engelder ZW, King WP, Do MN, Bashir R, Valera E, Каннингем БТ. Янкелоу А.М. и соавт. Аналитик. 2022 22 августа; 147 (17): 3838-3853. дои: 10.1039/d2an00438k. Аналитик. 2022. PMID: 35726910
Автоматизированные мультиплексные тесты на нуклеиновые кислоты для быстрого обнаружения инфекции SARS-CoV-2, гриппа A и B с помощью количественной ПЦР с прямой обратной транскрипцией (dirRT-qPCR) на центрифужной микрожидкостной платформе.

Ji M, Xia Y, Loo JF, Li L, Ho HP, He J, Gu D. Джи М и др. RSC Adv. 2020 15 сентября; 10 (56): 34088-34098. doi: 10.1039/d0ra04507a. Электронная коллекция 2020 10 сентября. RSC Adv. 2020. PMID: 35519051 Бесплатная статья ЧВК.
Просмотреть все статьи «Цитируется по»
термины MeSH
вещества
§ 89-5-33 — Общий указатель; прямое и обратное :: Кодекс штата Миссисипи 2013 г. :: Кодексы и статуты США :: Законодательство США :: Justia
Посмотреть Кодекс штата Миссисипи 2020 г. | Посмотреть предыдущие версии Кодекса штата Миссисипи
Кодекс MS § 89-5-33 (2013) Что это?
(1) Секретарь канцелярии составляет общий указатель, прямой и оборотный, в который вносятся в обычном алфавитном порядке под соответствующей буквой имя каждого производителя инструментов и имя каждого лицо, которому сделано; и в том же алфавитном порядке под соответствующим заголовком должны быть внесены имя каждого лица, для которого изготовлен инструмент, и имя каждого лица, которым изготовлен инструмент. Общий указатель, как прямой, так и обратный, закладных и договоров доверительного управления землей должен храниться отдельно от общего указателя для других записей, которые должен вести канцелярский клерк, и он должен делать в нем надлежащие записи по мере необходимости. сделать в другом общем индексе. Немедленно по получении любого документа, который должен быть зарегистрирован, клерк должен сделать эти записи в соответствующем общем указателе, и после регистрации документа напротив каждого имени, помещенного таким образом в такой общий указатель, должны быть отмечены книга и страница, на которой сделана запись. , как прямое, так и обратное.
Общий указатель, как прямой, так и обратный, закладных и договоров доверительного управления землей должен храниться отдельно от общего указателя для других записей, которые должен вести канцелярский клерк, и он должен делать в нем надлежащие записи по мере необходимости. сделать в другом общем индексе. Немедленно по получении любого документа, который должен быть зарегистрирован, клерк должен сделать эти записи в соответствующем общем указателе, и после регистрации документа напротив каждого имени, помещенного таким образом в такой общий указатель, должны быть отмечены книга и страница, на которой сделана запись. , как прямое, так и обратное.
(2) Секретарь канцелярии суда ведет раздельный указатель документов, описывающих землю, которые также внесены в общий указатель. Каждая запись должна содержать имя каждого изготовителя инструмента, имя каждого лица, которому он был сделан, а также дату, тип инструмента и соответствующую ссылку, если она записана. Напротив каждой такой записи индекс участка должен указывать местоположение земли, описанной в документе, (а) по квартальным участкам или государственным участкам или другим применимым подразделениям каждого участка, поселка и участка, установленным государственным обследованием, или (b) по участкам. номер для платных подразделений, официальных съемок и неофициальных подразделений и обычно используемых съемок. Секретарь может принять решение о сохранении раздельного указателя по разделам четверти четверти, а не по разделу четверти, но не должен требовать инструкции индексации составителя для описания раздела четверти четверти. Если иное не предусмотрено в настоящем разделе, каждый инструмент, описывающий землю и требующий внесения в общий указатель, также должен быть включен в раздельный указатель. В случае противоречия между общими и секционными указателями преимущественную силу имеет уведомление, сделанное по общему указателю, за исключением случаев, когда земля описывается номером лота для плановых подразделений, официальных съемок и неофициальных подразделений и широко используемых съемок, раздельный индекс имеет преимущественную силу.
номер для платных подразделений, официальных съемок и неофициальных подразделений и обычно используемых съемок. Секретарь может принять решение о сохранении раздельного указателя по разделам четверти четверти, а не по разделу четверти, но не должен требовать инструкции индексации составителя для описания раздела четверти четверти. Если иное не предусмотрено в настоящем разделе, каждый инструмент, описывающий землю и требующий внесения в общий указатель, также должен быть включен в раздельный указатель. В случае противоречия между общими и секционными указателями преимущественную силу имеет уведомление, сделанное по общему указателю, за исключением случаев, когда земля описывается номером лота для плановых подразделений, официальных съемок и неофициальных подразделений и широко используемых съемок, раздельный индекс имеет преимущественную силу.
(3) Каждый геодезист или другое лицо, которое подготавливает юридическое описание земли или подготавливает документ, используя существующее описание, и каждое лицо, подготавливающее доверительное управление, должно (за исключением случаев, предусмотренных настоящим документом) включать инструкцию по индексации, в которой указывается участок, поселок и участок, а также один или несколько участков квартала или государственных участков или другие применимые подразделения каждого участка, в котором расположена земля. Подготовитель, по своему выбору, может отметить четверть квартала, в котором находится земля, но не обязан это делать. Однако, если секции или квартальные секции, или государственные участки, или другие применимые подразделения секции не могут быть реально определены таким инспектором или другим лицом, инструкция по индексации должна содержать заявление об этом, а затем указывать все секции и четвертные секции. или государственные участки или другие применимые подразделения участка, в котором может быть расположен описываемый земельный участок. Инструкции по индексации должны быть четко выделены в документе так, чтобы они были легко видны служащему канцелярии. Клерк канцелярии должен отказать в приеме документа, который не содержит инструкции по индексации, требуемой в этом разделе, если документ иным образом не раскрывает информацию, которая должна быть включена в инструкцию по индексации. Чтобы документ был принят к учету, в нем должны быть указаны имя, адрес и номер телефона лица, организации или фирмы, подготовивших его.
Подготовитель, по своему выбору, может отметить четверть квартала, в котором находится земля, но не обязан это делать. Однако, если секции или квартальные секции, или государственные участки, или другие применимые подразделения секции не могут быть реально определены таким инспектором или другим лицом, инструкция по индексации должна содержать заявление об этом, а затем указывать все секции и четвертные секции. или государственные участки или другие применимые подразделения участка, в котором может быть расположен описываемый земельный участок. Инструкции по индексации должны быть четко выделены в документе так, чтобы они были легко видны служащему канцелярии. Клерк канцелярии должен отказать в приеме документа, который не содержит инструкции по индексации, требуемой в этом разделе, если документ иным образом не раскрывает информацию, которая должна быть включена в инструкцию по индексации. Чтобы документ был принят к учету, в нем должны быть указаны имя, адрес и номер телефона лица, организации или фирмы, подготовивших его. Если документ подготовлен поверенным, документ должен также включать номер адвоката в штате Миссисипи. Тот факт, что инструкция по индексированию или информация о подготовителе могут быть опущены, неверны, неполны или ложны, не делает документ недействительным или его подачу для регистрации. Клерк канцелярии должен внести документ в раздельный указатель в соответствии с инструкцией по индексации или равноценной информацией, если она принята к хранению без инструкции по индексации, и не должен делать никаких записей в каких-либо других квартальных разделах или государственных лотах или подразделениях раздела. Несмотря на вышеизложенное, следующие виды инструментов индексируются, как указано:
Если документ подготовлен поверенным, документ должен также включать номер адвоката в штате Миссисипи. Тот факт, что инструкция по индексированию или информация о подготовителе могут быть опущены, неверны, неполны или ложны, не делает документ недействительным или его подачу для регистрации. Клерк канцелярии должен внести документ в раздельный указатель в соответствии с инструкцией по индексации или равноценной информацией, если она принята к хранению без инструкции по индексации, и не должен делать никаких записей в каких-либо других квартальных разделах или государственных лотах или подразделениях раздела. Несмотря на вышеизложенное, следующие виды инструментов индексируются, как указано:
(a) Документы, описывающие землю со ссылкой на официально обозначенные подразделения или на официальные измерения или на неофициальные подразделения и обычно используемые измерения, не требуют инструкции по индексации и должны быть проиндексированы в общем указателе и индексном указателе для такого подразделения или обследования. без дополнительных требований.
без дополнительных требований.
(b) Документы, описывающие землю или интересы в земле исключительно посредством ссылки на ранее зарегистрированные документы или влияющие на ранее зарегистрированные инструменты, не требуют инструкции по индексации и не должны вноситься в раздельный указатель, но должны быть внесены в общий указатель и отмечены на маржа ранее зарегистрированного инструмента. Документы, описывающие землю или права на землю по конкретному описанию одних участков, а для других участков — по ссылкам на ранее зарегистрированные документы, должны быть внесены в раздельный указатель в соответствии с инструкцией по индексации для конкретного описания, а также отмечены на полях листа. ранее записанный инструмент, в дополнение к общему индексу.
(c) Документы, содержащие общие описания всех земель в пределах указанной географической области без конкретного описания, должны быть внесены в отдельную часть раздельного указателя или в указатель неопределен- ных записей или указатель общих транспортных средств в дополнение к общему указателю .
(d) Документы, описывающие землю в неравномерных участках (весь участок или часть участка, который нельзя разделить на четвертные участки для целей индексации), должны быть внесены в общий указатель и в соответствующий раздельный указатель, который ведет клерк канцелярии. Однако инструкция по индексации является надлежащей и полной, если в ней указывается не более чем номер участка или участков неправильной формы, на которых расположен земельный участок или, как указано выше, на которых этот земельный участок может быть расположен. Когда документ описывает землю в пределах неправильной секции в соответствии с официально установленными подразделениями или официальными съемками, или неофициальными подразделениями или широко используемыми съемками, он должен быть проиндексирован в индексе секций для таких подразделений или съемок.
(4) Когда инструмент был восстановлен для использования с микрофильма или другой архивной записи, канцелярский служащий должен сделать на полях пометку о том, что это замененная запись, и указать дату, когда он был восстановлен для использования. Такая пометка на полях представляет собой уведомление о том, что общий указатель должен быть проверен на предмет документов, поданных до такой даты, которые могли быть отмечены на полях исходной записи, но не указаны на полях восстановленной записи.
Такая пометка на полях представляет собой уведомление о том, что общий указатель должен быть проверен на предмет документов, поданных до такой даты, которые могли быть отмечены на полях исходной записи, но не указаны на полях восстановленной записи.
(5) Секретарь канцелярии суда вносит документы в секторальный указатель до конца двадцатого дня открытия офиса, следующего за днем подачи документа, за исключением записей о налоговых продажах.
(6) Если клерк канцелярии решит сокращать имена сторон документа в указателях, клерк должен вести список стандартных сокращений, используемых для этой цели, и должен придерживаться этого списка.
(7) Секретарь канцелярии суда не должен исправлять или изменять запись, сделанную в каком-либо указателе, независимо от того, ведется ли он вручную или с помощью компьютера, если только дата и время изменения четко не указаны в исправленной записи.
(8) Если недостаточно места для записей на полях зарегистрированного документа, канцелярист может сделать на полях ссылку, где находится дополнительный лист.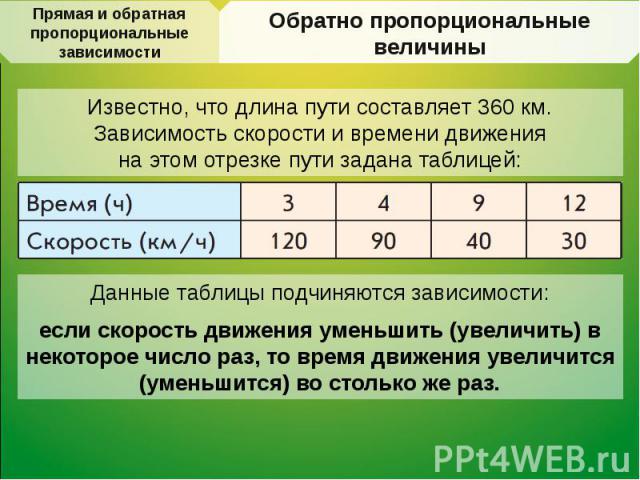
(9) За исключением случаев, прямо предусмотренных в настоящем документе, ничто, содержащееся в этом разделе, не должно толковаться как изменяющее требования других законодательных актов в отношении обязанностей клерка канцелярии индексировать и регистрировать документы, влияющие на право собственности на землю.
Отказ от ответственности: Эти коды могут быть не самой последней версии. Миссисипи может иметь более актуальную или точную информацию. Мы не даем никаких гарантий или гарантий относительно точности, полноты или адекватности информации, содержащейся на этом сайте, или информации, на которую есть ссылки на государственном сайте. Пожалуйста, проверьте официальные источники.
Концепция прямого и реверсивного кривошипа для V-образных и радиальных двигателей
Метод прямого и обратного вращения коленчатого вала применим к поршневым двигателям, т. е. V-образным двигателям, радиальным двигателям и т.
 д., в которых поршень совершает возвратно-поступательное движение.
д., в которых поршень совершает возвратно-поступательное движение.Как показано на рис.1 (радиальный двигатель) и рис.2 (клиновидный двигатель), шатуны соединены с общим кривошипом, и этот кривошип вращается только в одной плоскости. Следовательно, нет первичной или вторичной пары. Для балансировки требуется только первичная и вторичная сила.
- Метод прямого и обратного вращения коленчатого вала используется в поршневых двигателях для двух целей:
(1) Для определения первичных и вторичных неуравновешенных сил.
(2) Для уравновешивания первичных и вторичных неуравновешенных сил.
- На рис.3 показан механизм поршневого двигателя, в котором кривошип OC вращается с угловой скоростью ω\omegaω рад/с по часовой стрелке. Пусть θ\thetaθ — угол, который кривошип ОС составляет с линией хода цилиндра.
Рис-3
1. Первичная сила:-
- Первичная сила дисбаланса «FP» F_P «FP» определяется как,
FP=mrω2. 2} .cos\thetaFP=mrω2.cosθ
2} .cos\thetaFP=mrω2.cosθ
где m = масса возвратно-поступательных частей, кг
- Эта неуравновешенная первичная сила равна горизонтальной составляющей центробежной силы, создаваемой воображаемой массой ‘m’ , расположенной на шатунной шейке ‘C’, как показано на рис. рис.4.
Рис-4
- Схема, показанная на рис. 4 , может быть заменена другой компоновкой, показанной на рис. 5 , в которой OC называется фактическим кривошипом или первичным прямым кривошипом, а OCˊ называется косвенным кривошипом или первичным обратным ходом. рукоятка.
- Неуравновешенную первичную силу, вызванную массой m, можно определить, заменив массы m′2{‘m’\over2}2’m’ в зеркальном отображении, и этот метод замены массы m на Масса ′m′2{‘m’\over2}2′m′ называется прямым и обратным кривошипным методом.
Рис-5
Первичный прямой кривошип OC образует угол θ\thetaθ с линией хода и равномерно вращается на ‘ω\omegaω’ рад/с по часовой стрелке, тогда как первичный реверсивный кривошип OCˊ образует угол -θ\thetaθ с линией хода и вращается равномерно на ‘ω\omegaω’ рад/с против часовой стрелки, как показано на рис.
 5 . Таким образом, первичный реверсивный кривошип является зеркальным отражением основного прямого кривошипа.
5 . Таким образом, первичный реверсивный кривошип является зеркальным отражением основного прямого кривошипа.Параметры первичных прямых и обратных кривошипов:
I. Первичный прямой кривошип:
Угловое положение = θ\thetaθ
Угловая скорость = ω\omegaω (по часовой стрелке)
Радиус кривошипа = rII. Первичный обратный кривошип:
Угловое положение = -θ\thetaθ
Угловая скорость = ω\omegaω (против часовой стрелки)
Радиус кривошипа = r
Пусть масса ‘m’ возвратно-поступательных частей делится на две равные части (т.е. m2m\over22m).
Одна из деталей размещается на прямой шатунной шейке «С», а другая часть размещается на обратной шатунной шейке «С», как показано на рис.5.Центробежная сила, действующая на каждую массу, расположенную на прямой шатунной шейке С и обратной шатунной шейке
Cˊ=m2rω2Cˊ = {m\over2}r {\omega^2} Cˊ=2mrω2 92} × {r \ over4n} потому что 2 \ тета
\end{align}FSИли FS=mrω2.


 А увеличение числа наоборот ведет к уменьшению другого во столько же раз.
А увеличение числа наоборот ведет к уменьшению другого во столько же раз.


 Выход ретрансляции и связь RS485 являются дополнительными функциями.
Выход ретрансляции и связь RS485 являются дополнительными функциями. Также представлены универсальные входы/выходы «SUPER» и «SUPER2». Два порта связи RS-485 являются опцией.
Также представлены универсальные входы/выходы «SUPER» и «SUPER2». Два порта связи RS-485 являются опцией. Управление обогревом/охлаждением, выход ретрансляции, функция таймера и связь RS485 являются дополнительными функциями.
Управление обогревом/охлаждением, выход ретрансляции, функция таймера и связь RS485 являются дополнительными функциями. 01.2010. UTAdvanced UT52A является сменным продуктом.
01.2010. UTAdvanced UT52A является сменным продуктом. Чтобы узнать об использовании нами файлов cookie и о том, как вы можете управлять своими настройками файлов cookie, ознакомьтесь с нашей Политикой использования файлов cookie. Продолжая использовать веб-сайт, вы соглашаетесь на использование нами файлов cookie.
Чтобы узнать об использовании нами файлов cookie и о том, как вы можете управлять своими настройками файлов cookie, ознакомьтесь с нашей Политикой использования файлов cookie. Продолжая использовать веб-сайт, вы соглашаетесь на использование нами файлов cookie.
 регулятор давления прибора.
регулятор давления прибора. когда давление газа превышает выходное давление регулятора давления прибора.
когда давление газа превышает выходное давление регулятора давления прибора.
 …. обратное или прямое действие относится к выходному сигналу, который изменяется из-за входного сигнала (т.е. пневматический или DDC-термостат.) Переключатели будут просто классифицироваться как разомкнутые или замкнутые в зависимости от повышения или понижения входного сигнала (в данном случае давления газа).
…. обратное или прямое действие относится к выходному сигналу, который изменяется из-за входного сигнала (т.е. пневматический или DDC-термостат.) Переключатели будут просто классифицироваться как разомкнутые или замкнутые в зависимости от повышения или понижения входного сигнала (в данном случае давления газа). …. обратное или прямое действие относится к выходному сигналу, который изменяется из-за входного сигнала (т.е. пневматический или DDC-термостат.) Переключатели будут просто классифицироваться как открытые или закрытые в зависимости от подъема или падения входного сигнала (в данном случае давления газа).
…. обратное или прямое действие относится к выходному сигналу, который изменяется из-за входного сигнала (т.е. пневматический или DDC-термостат.) Переключатели будут просто классифицироваться как открытые или закрытые в зависимости от подъема или падения входного сигнала (в данном случае давления газа).


 Электронный адрес:
Электронный адрес: 

 Электронный адрес:
Электронный адрес:  BMC Infect Dis. 2017.
PMID: 29258444
Бесплатная статья ЧВК.
BMC Infect Dis. 2017.
PMID: 29258444
Бесплатная статья ЧВК. , Эль Сахли Х. М., Ронка С. Е., Мюррей К. О.
Горчаков Р. и соавт.
Am J Trop Med Hyg. 2019Февраль; 100 (2): 427-433. doi: 10.4269/ajtmh.18-0755.
Am J Trop Med Hyg. 2019.
PMID: 30560770
Бесплатная статья ЧВК.
, Эль Сахли Х. М., Ронка С. Е., Мюррей К. О.
Горчаков Р. и соавт.
Am J Trop Med Hyg. 2019Февраль; 100 (2): 427-433. doi: 10.4269/ajtmh.18-0755.
Am J Trop Med Hyg. 2019.
PMID: 30560770
Бесплатная статья ЧВК.

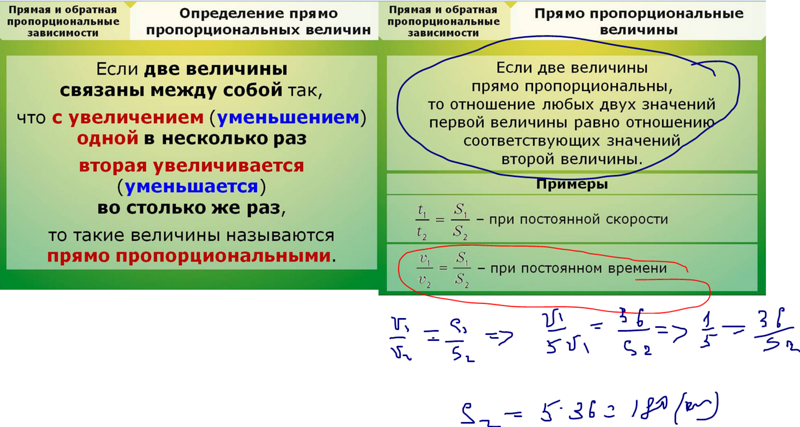
 д., в которых поршень совершает возвратно-поступательное движение.
д., в которых поршень совершает возвратно-поступательное движение. 5 . Таким образом, первичный реверсивный кривошип является зеркальным отражением основного прямого кривошипа.
5 . Таким образом, первичный реверсивный кривошип является зеркальным отражением основного прямого кривошипа.