РАСЧЁТ ГЛАВНОЙ БАЛКИ
1. Сбор нагрузок приведен в табл.3.
Таблица 3. Нагрузки на главную балку.
| Нагрузка | Нормативная | Коэф. надёжности | Расчётная | |
| кг/м2 | гН/м2 | гН/м2 | ||
| Постоянная t = 1,1см | 109,9 | 10,99 | 1,05 | 11,54 |
| Вт. балка (факт. I60Ш2) | 176,9 | 17,69 | 1,05 | 18,6 |
| Временная | 1,2 | |||

| 4286,8 | 428,68 | 510,14 |
2. Сечение главной балки формируем из двух поясов из листов,
соединённых друг с другом стенкой из листа. Затем и проверяем её прочность и устойчивость.
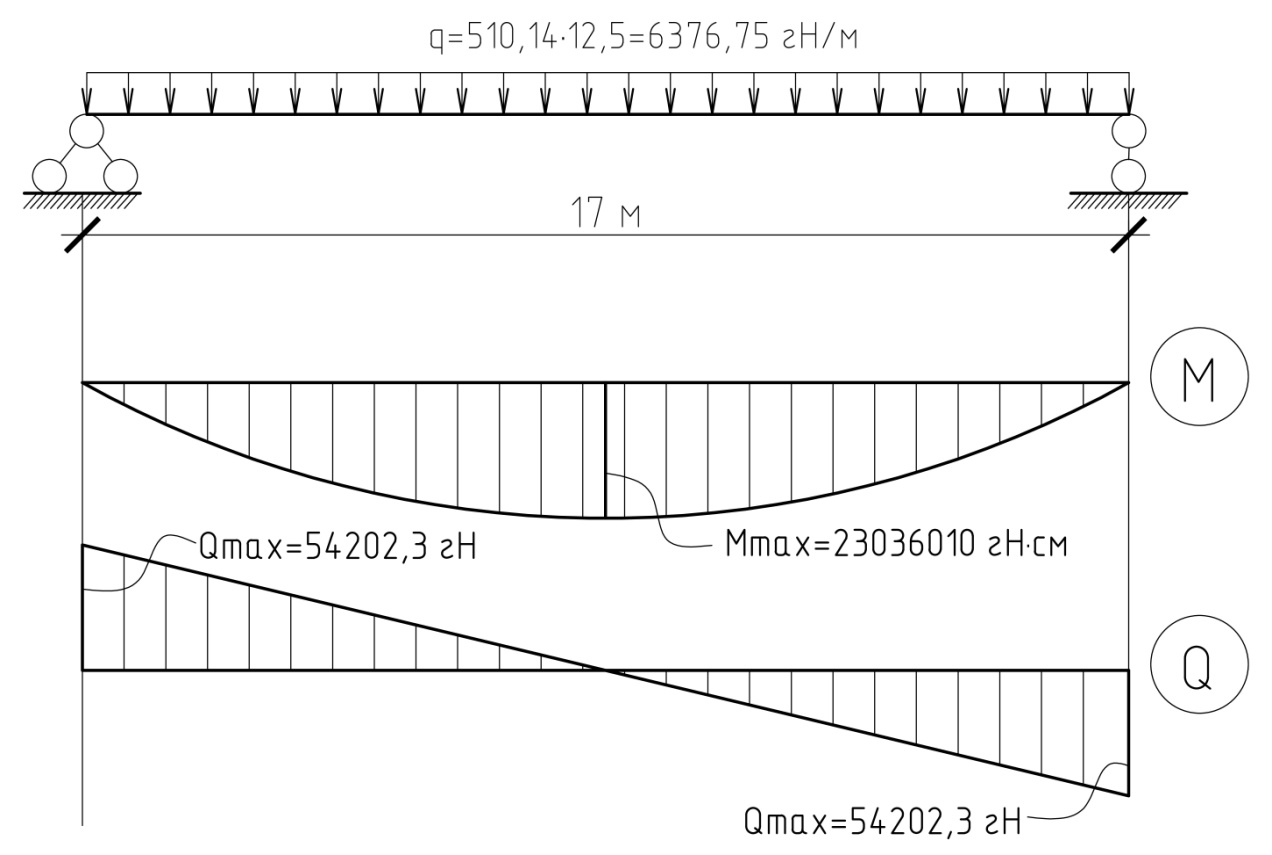 Расчётная схема главной балки показана на рис. 4
Расчётная схема главной балки показана на рис. 4
Рис. 4. Расчётная схема шарнирно-опёртой главной балки
3. Линейная нагрузка гН/м на единицу длины главной балки
ü расчётная: q=510,14·12,5=6376,75 гН/м;
ü нормативная: qн=428,68·12,5=5358,5 гН/м.
4. Для главной балки принимаем малоуглеродистую сталь спокойной плавкимарки В Ст3сп5 (ГОСТ 27772-88) ( Rу=230 МПа).
5. Расчётный изгибающий момент
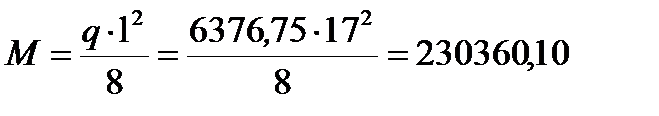 гН·м;
гН·м;
поперечная сила  гН;
гН;
нормативный изгибающий момент
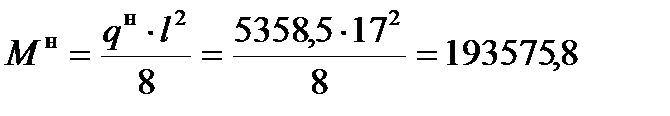 гН·м.
гН·м.
Последовательность расчета поперечного сечения двутавровой сварной балки.
1. Из условия прочности на изгиб находим момент сопротивления
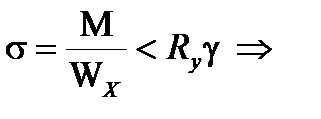

2. Определяем площадь сечения стенки tст. из условия прочности на

тогда минимальная толщина стенки при гибкости 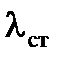 =120…130, принимаем
=120…130, принимаем 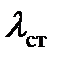 =130 , чтобы стенка была не слишком гибкой, тем самым исключить применение большого количества рёбер жесткости.
=130 , чтобы стенка была не слишком гибкой, тем самым исключить применение большого количества рёбер жесткости.

3. Находим толщину стенки в зависимости от момента сопротивления
при заданной гибкости Þ

назначаем толщину стенки кратно 0,2 см Þ t =2,2  .
.
4. Требуемая площадь сечения балки должна быть не менее
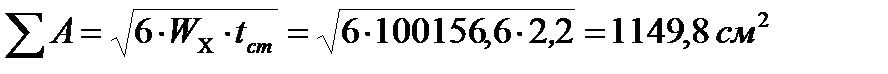
5. Площадь сечения стенки (50%) – 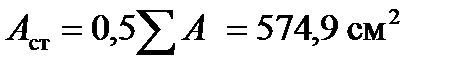 , тогда
, тогда
Þ оптимальная высота 
назначаем высоту стенки hст кратно 5 смÞ hст=265 см,
а высоту сечения балки Þ 
6. Площадь каждого пояса (25%) равна 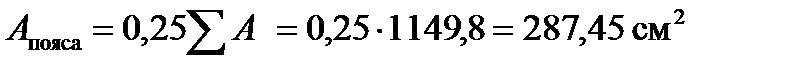
При tп=3,2см его ширина
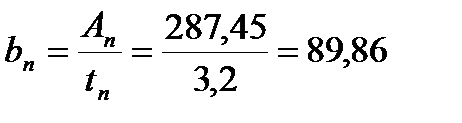 см, принимаем: Þ b
см, принимаем: Þ b
Отношение ширины пояса bпк его толщине tп для малоуглеродистой стали должно быть не более 30.
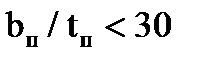
Принимаем tп =3,2 см, тогда 90/3,2=28,3 см < 30 см.
7. Фактическая площадь сечения двух поясов и стенки
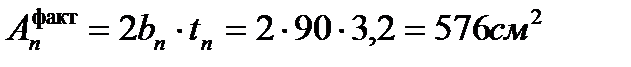
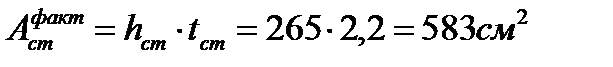
8. Суммарная площадь всего сечения
 .
.
9. Находим главный момент инерции и момент сопротивления сечения
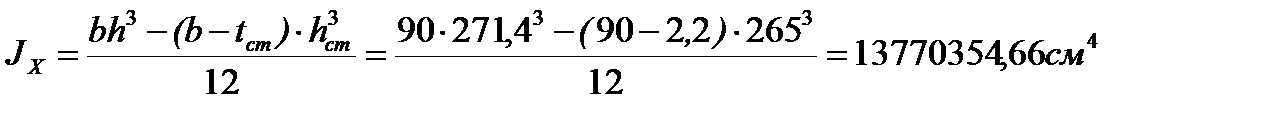
10. Момент сопротивления балки
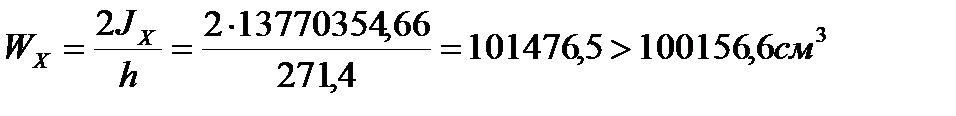
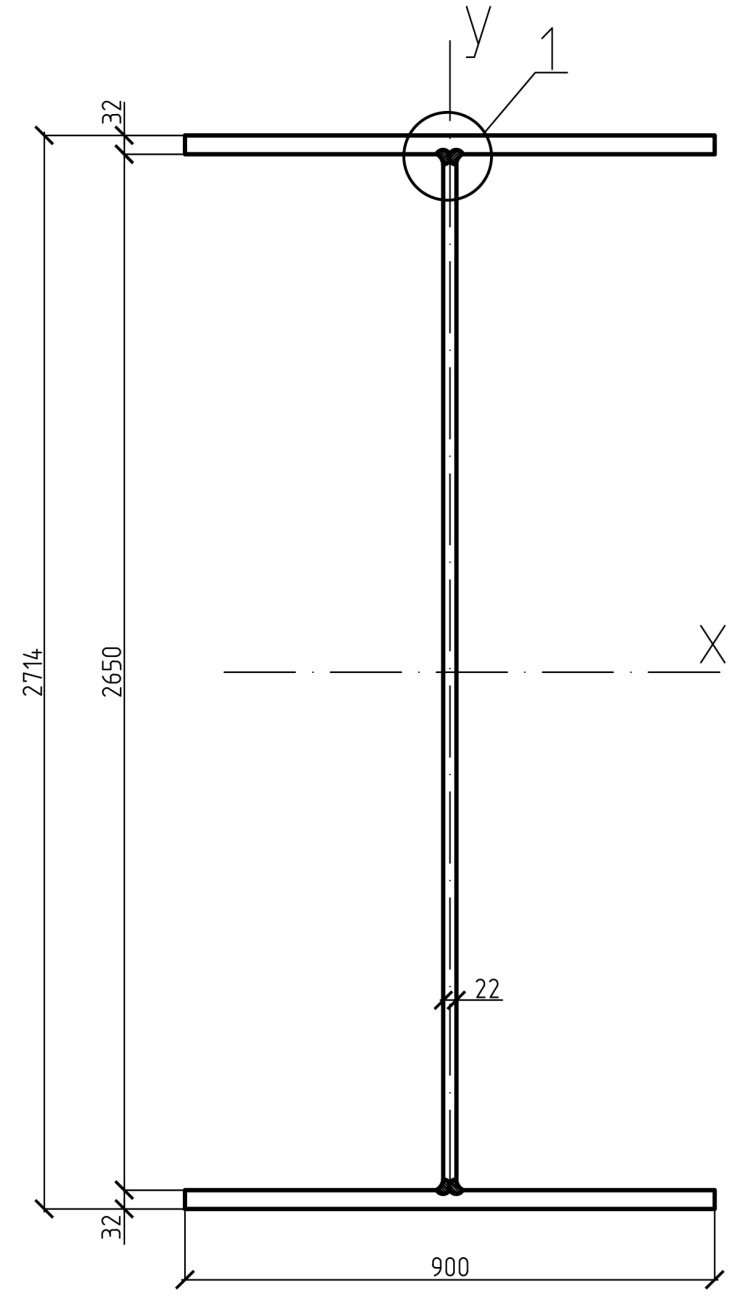 а) б)
а) б)

Рис. 5. Сечение сварной главной балки из трёх листов.
11. Проверяем прочность при изгибе главной балки в середине её
пролёта:
 ,
, 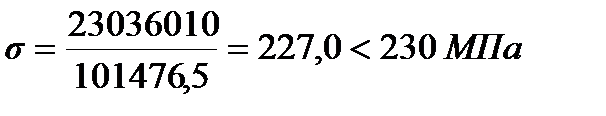
прочность сечения главной балки при действии максимального изгибающего момента обеспечена.
12. Статический момент половины сечения балки равен:

тогда максимальные сдвигающие напряжения по нейтральной оси стенки 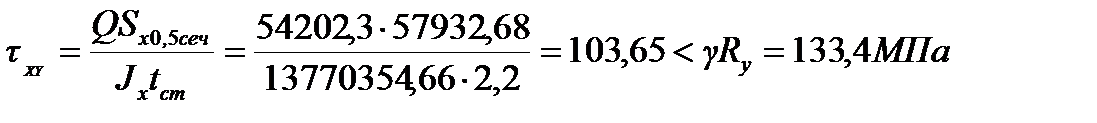 прочность на срез обеспечена.
прочность на срез обеспечена.
13. Поверка прочности шва, соединяющего пояс со стенкой, на срез.
Шов выполнен с полным проваром.
Статический момент полки: 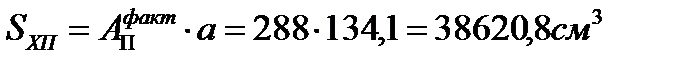 где а – расстояние от главной оси Х до центра тяжести пояса.
где а – расстояние от главной оси Х до центра тяжести пояса.
Величина сдвигающих напряжений в сварном шве в зоне сплавления  прочность на срез обеспечена.
прочность на срез обеспечена.
Относительный прогиб сварной двутавровой балки из листов  жёсткость достаточна, так как относительный прогиб меньше величины ограничиваемой нормами СНиП «Нагрузки и воздействия».
жёсткость достаточна, так как относительный прогиб меньше величины ограничиваемой нормами СНиП «Нагрузки и воздействия».

4. СОВЕРШЕНСТВОВАНИЕ ГЛАВНОЙ БАЛКИ
(замена поясов балки из сварных листов на пояса из тавров).
1. Назначаем площадь сечения каждого из тавров:
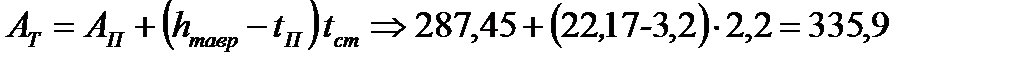 см2
см2
принимаем два симметричных тавра 20КТ12(ТУ Н-2-24-72):
ü габариты h´b = 24,01´42,67 см;
ü масса m = 256 кг/м;
ü площадь сечения каждого тавра AТ = 326 см2 ;
ü момент инерции Jx =10300 см4; z0 =5,51 см;
ü толщина стенки тавра d=3,75 см;
ü толщина полки тавра t = 6,0 см.
ü расстояние от центра тяжести тавра до главной оси
 =24,01-5,51 = 18,5 см;
=24,01-5,51 = 18,5 см;
2. Определяем площадь сечения вставки из листа при  = 101476,5 см3
= 101476,5 см3
 1159 — 2·326=507 см2
1159 — 2·326=507 см2
3. Вычисляем высоту вставки из листа, заменяя двутавр с поясами из листов на двутавр с поясами из тавров при  = 101476,5 см3
= 101476,5 см3
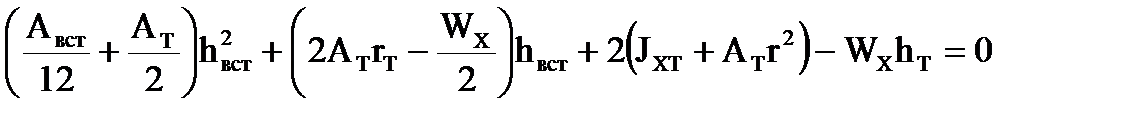
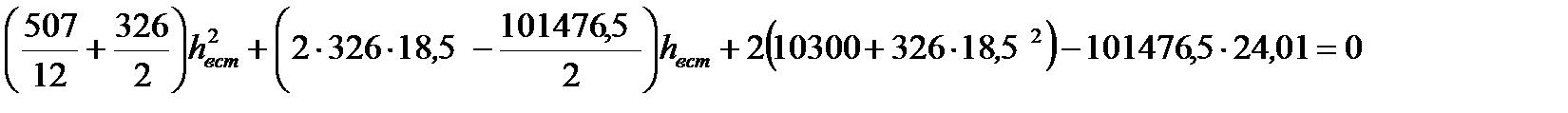
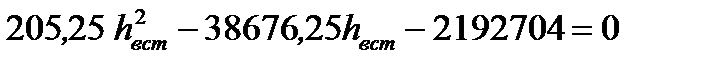

 получили высоту вставки
получили высоту вставки 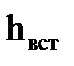 = 235 см и высоту сечения балки
= 235 см и высоту сечения балки
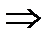 H = hвст+ 2 hТ ; H = 235 + 2·24,01 =283,02 см.
H = hвст+ 2 hТ ; H = 235 + 2·24,01 =283,02 см.
4. Вычисляем главный момент инерции двутавра с поясам из тавров:

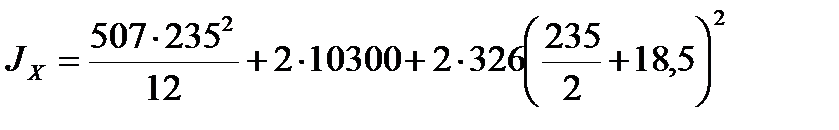 =14413284,3 см4 > 13770354,66см4
=14413284,3 см4 > 13770354,66см4
и момент сопротивления балки:

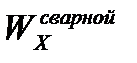 =101476,5 см3.
=101476,5 см3.
Сравнение показывает, что замена двутавра с поясами из листов на двутавр с поясами из тавров выполнена точно. Следовательно, прочность при изгибе нового двутавра с поясами из тавров достаточна и относительная жёсткость его также достаточна. Повторная проверка не требуется.
По приведённому алгоритму разработана программа автоматического расчёта двутавровой балки.
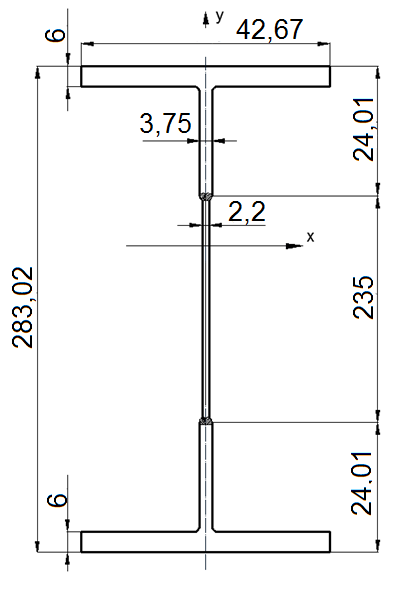
Рис. 6. Сечение главной балки из тавров.
5. СОВЕРШЕНСТВОВАНИЕ ГЛАВНОЙ БАЛКИ
(замена поясов балки из листов на пояса из уголков (4 шт.)).
В состав пояса входят поясные уголки, которые примем равнополочными. Калибр уголков (ширина их полок bуг) устанавливают в зависимости от мощности балки и способа передачи нагрузки на нее.
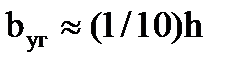
Толщину поясных уголков удобно принимать равной толщине стенки tуг=tст, так как это облегчает устройство монтажных стыков.
При наличии в составе сечения балки горизонтальных листов, необходимо , чтобы поясные уголки обеспечивали надежную передачу усилий пояса на стенку. Для этого площадь сечения двух уголков пояса рекомендуется принимать не менее 30% всей площади сечения пояса.
1. 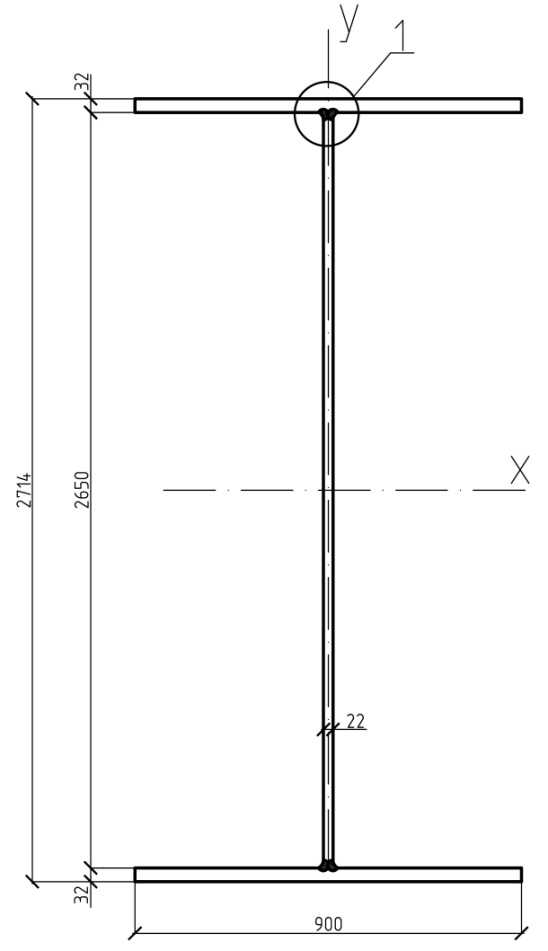 Аст=583см2;
Аст=583см2;
2. 2Ап=576 см2;
3. 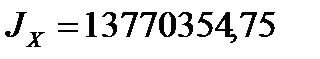 см4;
см4;
4. Wx=101476 см3;
Рис. 7. Сечение сварной главной балки из трёх листов.
Каждый из поясов заменяем двумя уголками 2L250*30 (АL=223 см2;
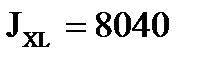 см4; zo=6,07 см) ГОСТ 8509-86 .
см4; zo=6,07 см) ГОСТ 8509-86 .
1. Находим высоту сечения новой балки из уравнения
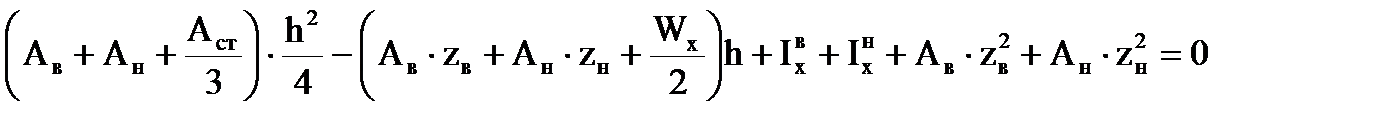
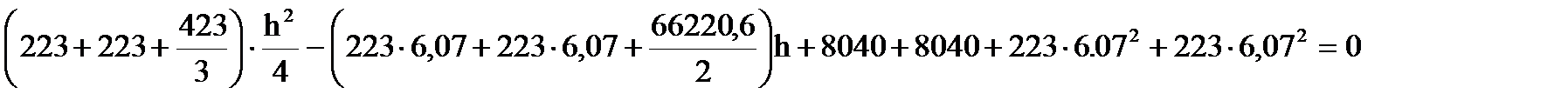


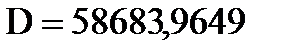
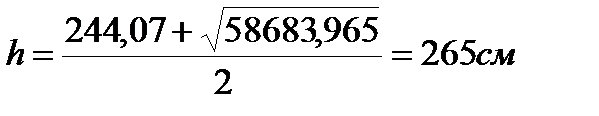
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
1 Порядок расчета сварной двутавровой балки
Определить высоту балки:
– построить эпюры сил и моментов;
– найти опасное сечение;
– определить высоту балки из условий жесткости;
– определить высоту балки из условий прочности и экономичности;
– откорректировать высоту балки при недогрузе и округлить до значения, кратного 50 мм.
Спроектировать сечение балки.
Проверить сечение балки:
– по распределению металла;
– по прочности.
Обеспечить общую и местную устойчивость балки: рассчитать, спроектировать, расставить вертикальные и горизонтальные ребра жесткости.
Рассчитать или назначить параметры сварных соединений балки.
Спроектировать необходимые стыки балки: конструктивные, технологические и монтажные.
Спроектировать и рассчитать опорные части балки.
Рассчитать вес основного и наплавленного металла.
Вычертить балку в масштабе 1:100 с необходимыми разрезами, сечениями, размерами и условными обозначениями, необходимыми для изготовления и монтажа балки.
2 Расчета сварной двутавровой балки
2.1 Задание на проектирование сварной двутавровой балки
Спроектировать сварную двутавровую балку при следующих параметрах:
L = 4,5 м;q1 = 15 КН/м;P =50 КН; [σр] = 225 МПа; [τср] = 135 МПа;
fmax /l= 1/500; Материал – 14Г2; Нагрузка статическая.
Рис.1 Расчетная схема балки


2.2 Определение высоты балки
Для определения опорных реакций составим уравнения моментов относительно точек А иВ:
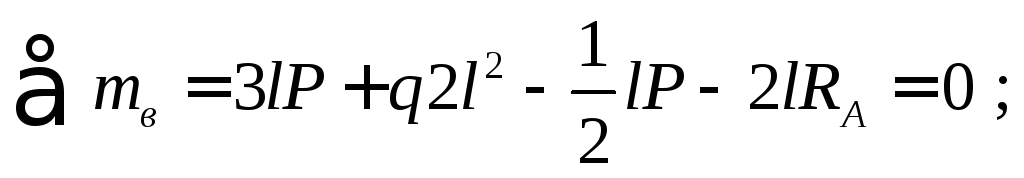
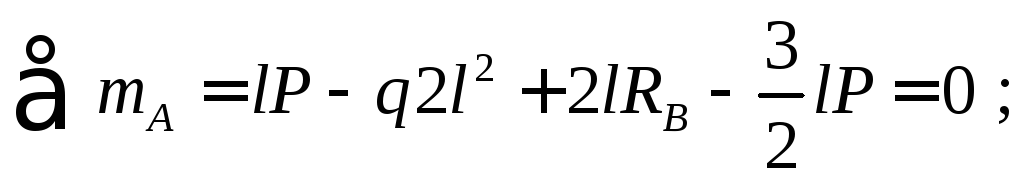
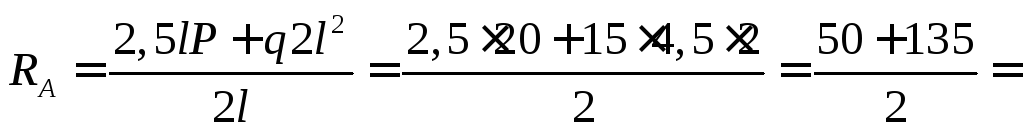
= 92,5 кН;
 кН.
кН.
Для определения внутренних силовых факторов и моментов применяем метод сечений.
Определим поперечные усилия Qв данной балке:
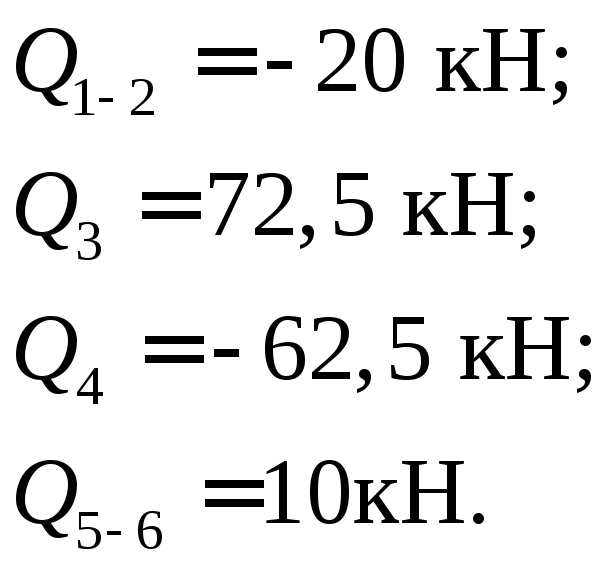
Определим изгибающие моменты Мв данной балке:

Анализ эпюр Qyи Mxпоказывает, что опасным сечением является сечениеС, где
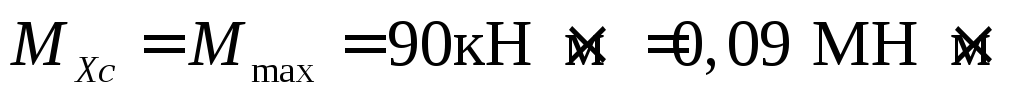 .
.
Определяем высоту балки из условий жесткости:
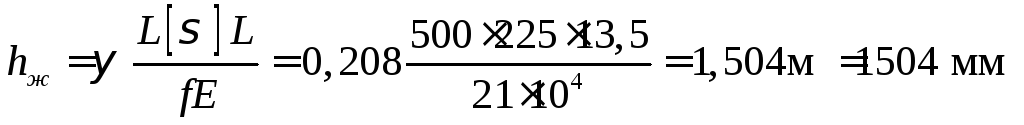 .
.
Определяем высоту балки из условия прочности и экономичности:
 .
.
В данном случае  ,
поэтому в соответствии с рекомендациями
принимаем высоту балки из условия
жесткости.
,
поэтому в соответствии с рекомендациями
принимаем высоту балки из условия
жесткости.
Округляем и принимаем  .
.
2.3 Расчет и проектирование сечения балки
Толщина стенки двутавровой балки:
 .
.
Принимаем δв = 10 мм.
Толщина пояса :
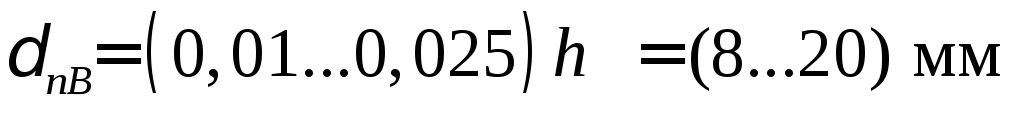 .
.
Предварительно принимаем δп = 25 мм.
Ширина пояса :
Для обеспечения местной устойчивости полок сжатого пояса рекомендуется:
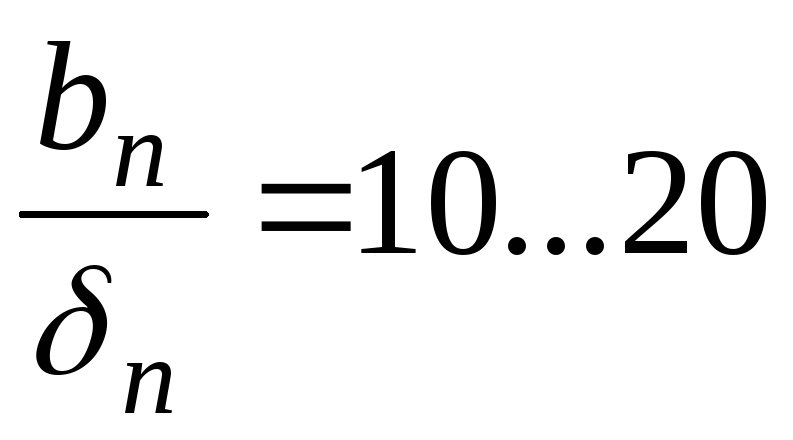 ,
,
поэтому еще одно значение bn: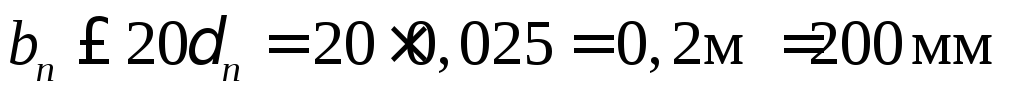 .
.
Кроме того, в поясах балки должно быть не меньше 30 % металла. Из этих соображений:
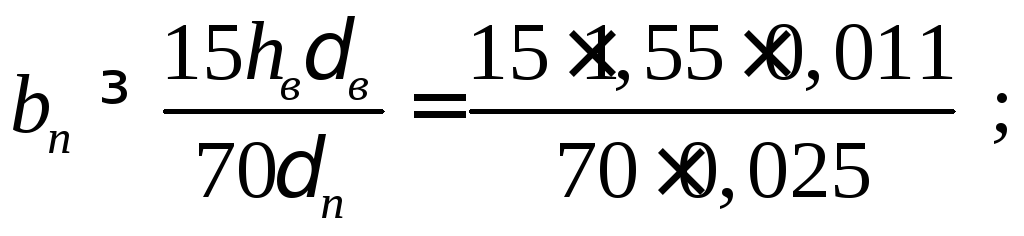
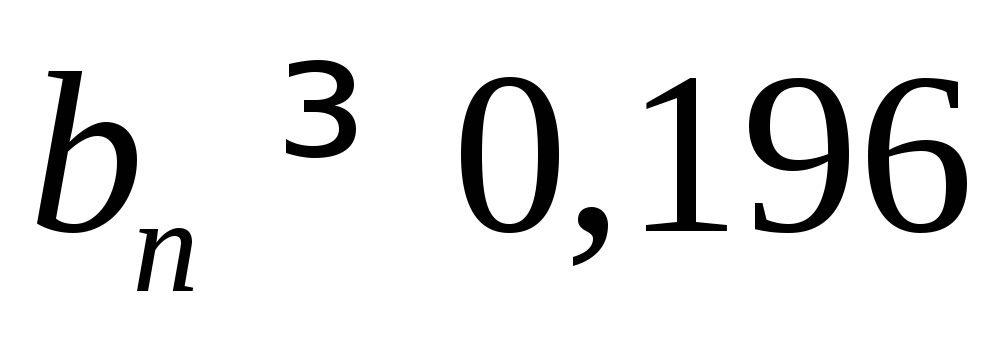 м = 196 мм .
м = 196 мм .
Учитывая то, что по ГОСТ 6009–74 стальная горячекатаная лента (полоса) при ширине свыше 140 мм выпускается с минимальной толщиной 25 мм, откорректируем размеры пояса, приняв полосу толщиной 25 мм и шириной 180 мм.
Принимаем размеры сечения балки:
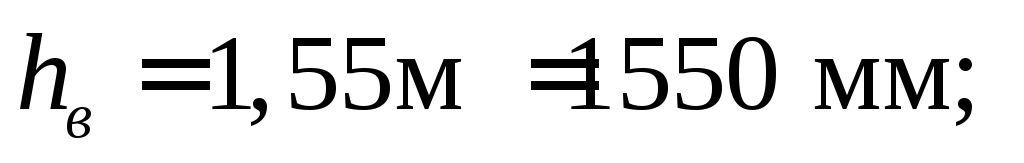
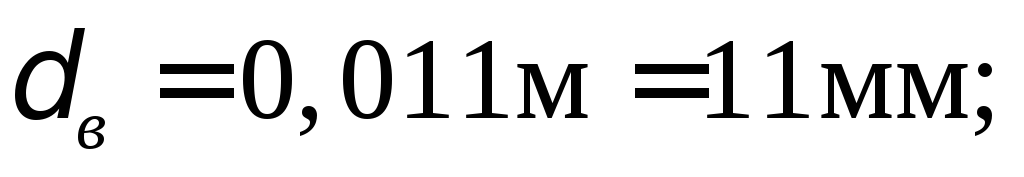
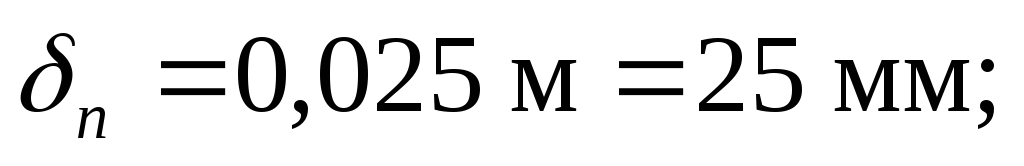
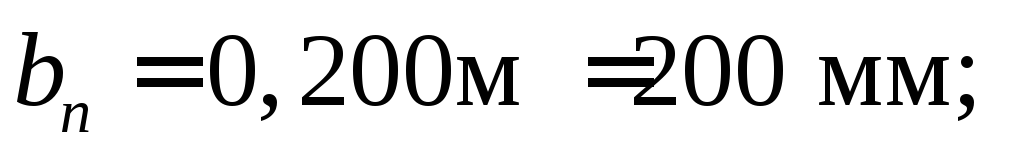
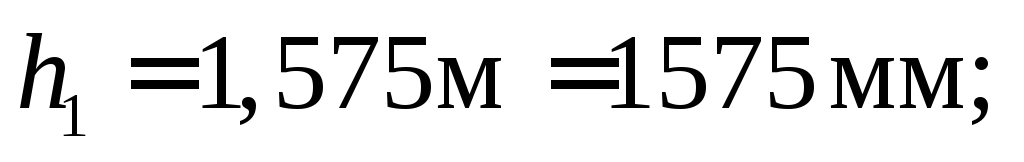

Уточнив все размеры сечения, определим истинный момент инерции сечения балки:
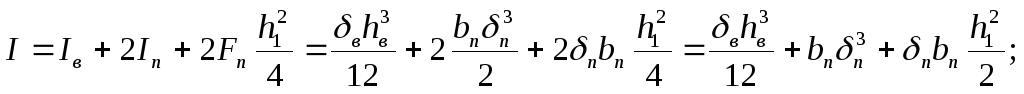

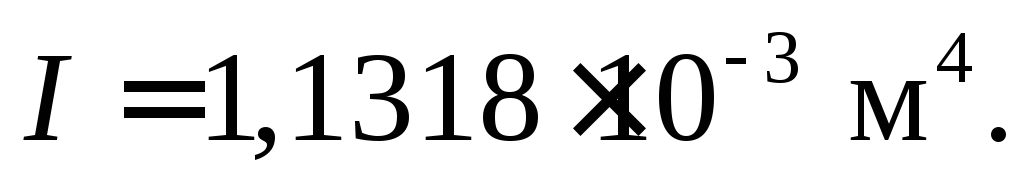
2.4 Проверка сечения балки
Выполним четыре проверки сечения
1 По использованию материала (в поясах должно быть не менее 30 % материала):

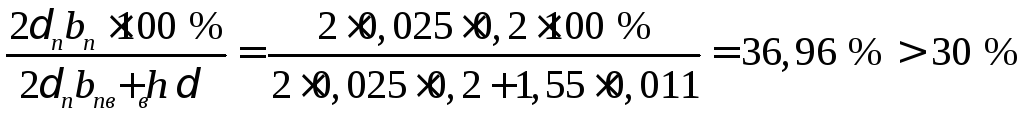 .
.
2 По максимальным изгибающим напряжениям:
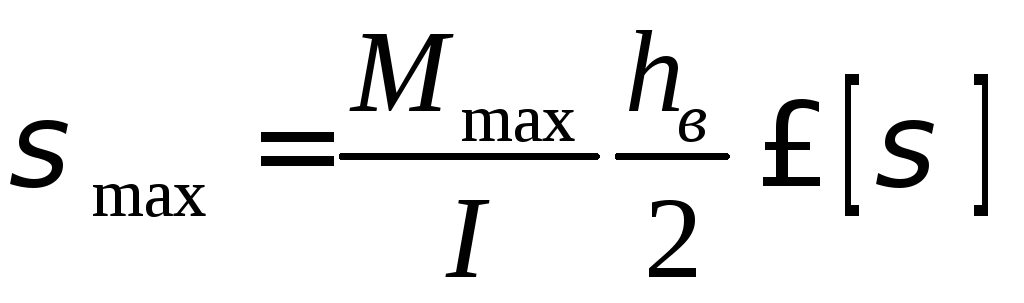 ;
;

3 По максимальным касательным напряжениям:
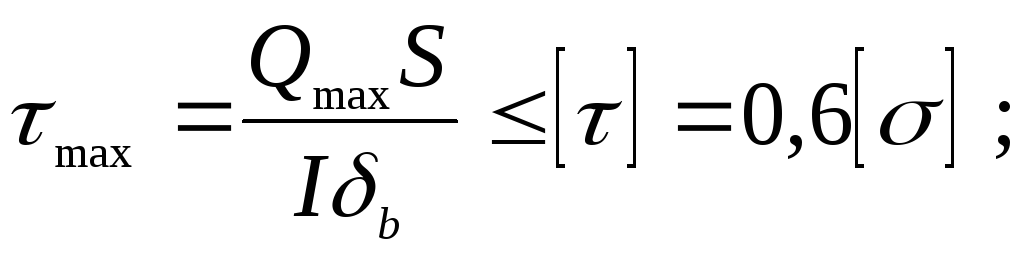


4. По эквивалентным напряжениям в верхней кромке стенки балки:

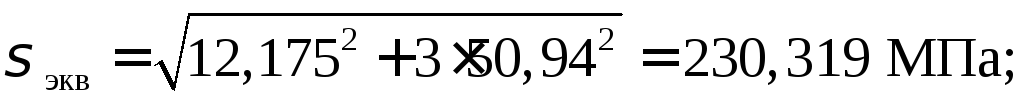
230,319 МПа < 225 МПа.
Балка перегружена. Перегруз оправдан выбором высоты балки из условия жесткости. Окончательные размеры балки:


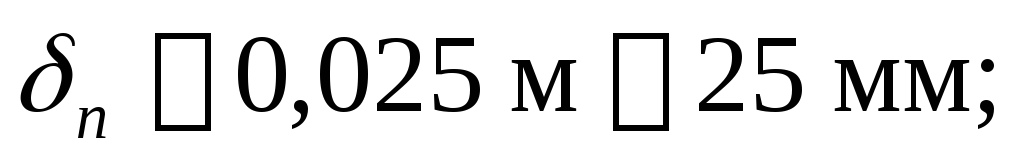

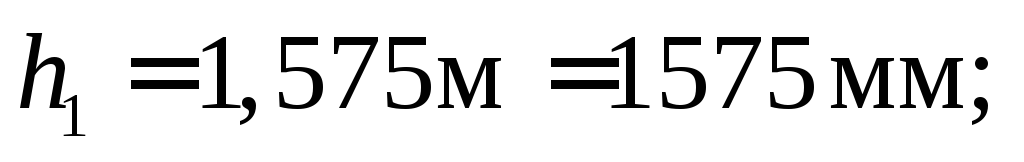
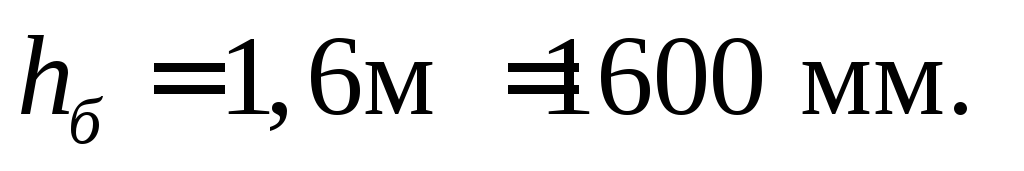
Расчёт сечения сварного двутавра

Tyhig
размещено: 31 Июля 2018обновлено: 12 Ноября 2018 Реализован расчёт сварных швов сварного двутавра.
Добавлен расчет прочности двутавра в плоскости изгиба вокруг оси x.
Исправлена ошибка с назначением разных сталей (было не назначить некоторые толщины листов).
20.08.2018 добавлен расчет Iy и т.п.
2.11.2018 добавлен расчет общей устойчивости по п. 8.4.1 (чистый изгиб) только в одной плоскости. С ошибками.
12.11.2018 Расчёт общей устойчивости исправлен, но двухсимметричные двутавры с разными полками считаются с ошибкой 10% (у меня кисп на 10% лучше, чем у Кристалла).
Планируется в далёком будущем реализация общей устойчивости, местной устойчивости пояса и стенки, проверка шага поперечных ребер.
Планируется в далёком будущем по замечаниям пользователей скорее всего одноразовая доработка интерфейса и расчетов. Так что жду конструктивные замечания.
Написано по мотивам по http://al-vo.ru/mekhanika/svarnaya-balka.html (большое спасибо автору). Его сайт и ексель ничем не плохи, просто хотелось написать свой калькулятор с более широкими возможностями.
Коэффициенты βf и βz учтены в расчете сварного шва только как для ручной сварки и сами не изменяются. При учете автоматической сварки проволокой коэффициенты надо изменять вручную в теле расчётов.
Сварные швы учтены без разделки кромок (см. Пособие к СНиП, оно не учтено) !
Характеристики двутавра (по моей лени) вычисляются пока только в вертикальной плоскости относительно оси х и без кручения.
По возможности, старался сделать расчёты как для биметаллической балки. Но в процессе задолбался и где-то мог упустить разницу. Для разных сталей сечения надо проверять ссылки на материал пояса и стенки.
Не реализовано ослабление сечения, но пока и не планируется.
Замеченная разница с Кристалл SCADа 21.1.3.1 от 14.04.2017 года:
1) Кристалл неправильно считает сварные швы, ошибается в 160 раз не в запас.
2) Кристалл возможно неправильно считает приведённые напряжения (п. 8.2.1 СП 16) в стенке балки, видимо, не учитывая центральную точку сечения (у меня расчёт по 3 точкам, в Кристалле получается по 1 или 2). У Кристалла Кисп на 10% меньше, то есть тоже не в запас.
3) Погрешность расчётов в паре тестах показала разницу около 2%, в обоих случаях у меня было хуже Кристалла. При этом старался не использовать округление, а вот что там в Кристалле реализовали никто не знает. Эту фразу написал для любителей брать балки с Кисп=0,98, если их ещё не пересажали.

а – схема изменения сечения по длине балки; б – сечение балки и эпюры напряжений.
Цель: Проверка режима расчета сопротивления сечений в постпроцессоре «Сталь» вычислительного комплекса SCAD
Задача: Проверить расчетное сечение сварного двутаврового профиля для главных балок пролетом 18 м в балочной клетке нормального типа. Верхний пояс главных балок раскреплен балками настила, расположенными с шагом 1,125 м.
Источник: Металлические конструкции : учебник для студ. Учреждений высш. проф. Образования / [Ю. И. Кудишин, Е. И. Беленя, В. С. Игнатьева и др.] ; под. Ред. Ю. И. Кудишина. — 13-е изд., испр. — М. : Издательский центр «Академия», 2011. С 195.
Соответствие нормативным документам: СНиП II-23-81*, СП 16.13330, ДБН В.2.6-163:2010.
Имя файла с исходными данными:
4.1 SectionResistance_Example_4.1.spr;
отчет — 4.1 SectionResistance_Example_4.1.doc
Исходные данные:
| M1 = 3469,28 кНм | Расчетный изгибающий момент; |
| Q1 = 925 кН | Расчетная перерезывающая сила; |
| Ry = 23 кН/cм2, Rs = 0,58*23=13,3 кН/cм2 | Сталь марки C255 при толщине t>20 мм; |
| l = 18 м | Пролет балки; |
| Wy = 15187,794 см3 | Геометрические характеристики для сварного |
| Iy = 1290962,5 см4 Sy = 9108,75 см3 iy = 63,715 см, iz = 4,265 см | двутавра с полками 240×25 мм и стенкой 1650×12 мм; |
Параметры SCAD Постпроцессор СТАЛЬ:
[Элемент № 1] Усилия
N Макс. 0 Т | My Макс. 0 Т*м | Mz Макс. 0 Т*м |
Mk Макс. 0 Т*м | Qz Макс. 94,31 Т
| Qy Макс. 0 Т |
| Длина стержня 3,75 м |
|
Расчет выполнен по СНиП II-23-81*
Конструктивный элемент Section
Сталь: C255
Длина элемента 3,75 м
Предельная гибкость для сжатых элементов: 220
Предельная гибкость для растянутых элементов: 300
Коэффициент условий работы 1
Коэффициент надежности по ответственности 1
Расчетная длина в плоскости XoY 1,125 м
Расчетная длина в плоскости XoZ 18 м
Расстояние между точками раскрепления на плоскости 1,125 м
Сечение

Результаты расчета | Проверка | Коэффициент использования |
|---|---|---|
п.5.12 | Прочность при действии изгибающего момента My | 0,99 |
пп.5.12,5.18 | Прочность при действии поперечной силы Qz | 0,41 |
пп.5.24,5.25 | Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики | 0,99 |
п. 5.14* | Прочность по приведенным напряжениям при одновременном действии изгибающего момента и поперечной силы | 0,86 |
п.5.15 | Устойчивость плоской формы изгиба | 0,99 |
пп.6.15,6.16 | Предельная гибкость в плоскости XoY | 0,09 |
пп.6.15,6.16 | Предельная гибкость в плоскости XoZ | 0,09 |
Коэффициент использования 0,99 — Прочность при действии изгибающего момента My
Ручной расчет (СНиП II-23-81*)
1. Необходимый момент сопротивления балки:
\[ W_{nes} =\frac{M_{\max } }{R_{y} \gamma_{c} }=\frac{\mbox{3469},\mbox{28}\cdot 100}{23}=15083,826 \quad см^{3}. \]
2. Максимальные касательные напряжения, возникающие в опорном сечении балки:
\[ \tau_{\max } =\frac{Q_{\max } S_{y} }{I_{y} t_{w} }=\frac{925\cdot 9108,75}{1290962,5\cdot 1,2}=5,4388 \quad кН/см^{2}. \]
3. Приведенные напряжения в рассматриваемом сечении балки:
\[ \sigma_{y} =\frac{M_{y} }{I_{y} }\frac{h_{w} }{2}=\frac{3469,28\cdot 100\cdot 165}{1290962,5\cdot 2}=22,1707 \quad кН/см^{2} \] \[ \tau_{yz} =\frac{Q_{z} S_{yf} }{I_{y} t_{w} }=\frac{925\cdot \left( {24\cdot 2,5\cdot \left( {0,5\cdot 165+0,5\cdot 2,5} \right)} \right)}{1290962,5\cdot 1,2}=3,00 \quad кН/см^{2} \] \[\sigma_{red} =\sqrt {\sigma_{y}^{2} +3\tau_{yz}^{2} } =\sqrt {22,1707^{2}+3\cdot 3,00^{2}} =22,7715 \quad кН/см^{2} \]
4. Гибкость элемента в плоскости действия момента:
\[ \lambda_{y} =\frac{\mu l}{i_{y} }=\frac{18\cdot 100}{63,715}=28,2508. \]
5. Гибкость элемента из плоскости действия момента:
\[ \lambda_{y} =\frac{\mu l}{i_{y} }=\frac{1,125\cdot 100}{4,265}=26,3775. \]
Сравнение решений
Фактор | Источник | Ручной счет | SCAD | Отклонение от ручного счета, % |
|---|---|---|---|---|
Прочность при действии изгибающего момента Му | 0,99 | 15083,826/15187,794 = 0,993 | 0,993 | 0,0 |
Прочность при действии поперечной силы Qz | – | 5,4388/13,3 = 0,4089 | 0,408 | 0,0 |
Прочность по приведенным напряжениям | – | 22,7715/1,15/23 = 0,861 | 0,861 | 0,0 |
Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики | – | 15083,826/15187,794 = 0,993 | 0,993 | 0,0 |
Устойчивость плоской формы изгиба | – | 15083,826/1/15187,794 = 0,993 | 0,993 | 0,0 |
Предельная гибкость в плоскости XoY | – | 26,3775/300 = 0,088 | 0,088 | 0,0 |
Предельная гибкость в плоскости XoZ | – | 28,2508/300 = 0,094 | 0,094 | 0,0 |
Расчет и проектирование двутавровой балки
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
СВЕРДЛОВСКОЙ ОБЛАСТИ
Государственное автономное образовательное учреждение
Среднего профессионального образования
Свердловской области
«НИЖНЕТАГИЛЬСКИЙ техникум металлообрабатывающих производств и сервиса»
Допустить к защите Руководитель МО _____________ /Зашляпина Н.Л. (подпись) «_____»____________ 20___ г. |
спроектировать двутавровую балку
Курсовой проект
Пояснительная записка
Специальность: | 150203 Сварочное производство
|
Выполнил студент | группа 501 | ПушкинА. А | |
(группа) | (подпись) | Ф.И.О. | |
Руководитель | преподаватель | Зашляпина Н. Л. | |
ученая степень, должность | (подпись) | Ф.И.О. | |
Консультант | преподаватель | Гриценко Н.В. |
2014
СОДЕРЖАНИЕ
ВВЕДЕНИЕ ……………………………………………………….…… | 3 |
1 ОСНОВНАЯ ЧАСТЬ …………………………………………….… | 5 |
1.1 Технологическая часть……………………… | 5 |
1.1.1 Описание конструкции …………………………………………. | 5 |
1.1.2 Выбор материала конструкции ……………………………….. | 6 |
1.1.3 Выбор способа сварки …………………………………………. | 7 |
1.1.4 Выбор сварочных материалов …………………………………. | 8 |
1.1.5 Технология изготовления и монтажа конструкции …………… | 10 |
1.2 Расчетная часть ……………………………………………….…… | 12 |
1.2.1 Определение расчётных усилий ……………………………….. | 12 |
1.2.2 Определение требуемой высоты балки | 13 |
1.2.3 Определение момента инерции …………………………….…… | 16 |
1.2.4 Определение напряжений ………………………………………. | 19 |
1.2.5 Определение катета шва ………………………………………… | 27 |
ЗАКЛЮЧЕНИЕ ………………………………………………………. | 28 |
ИСПОЛЬЗУЕМЫЕ ИСТОЧНИКИ ЛИТЕРАТУРЫ …………… | 29 |
ВВЕДЕНИЕ
Проектирование быстровозводимых зданий на современном этапе требует применения в качестве несущего каркаса стальных балок, поскольку при больших пролетах, от семи и больше метров, другие конструкции становятся неэффективными. Кроме этого существует еще целый ряд сооружений, где нет возможности использовать другие материалы, в частности – железобетонные конструкции.
Одним из лучших вариантов стальных балок является двутавровая балка. Она главным образом применяется для перекрытия больших пролетов промышленных и других зданий (4-18 метров), а также при создании эстакад, мостов, рабочих площадок и других металлических сооружений. Почему данный металлопрокатный продукт столь популярен? Прежде всего, это, безусловно, обширный спектр использования подобного изделия. Применение двутавровой стальной балки встречается в качестве прочных строительных металлоконструкции, что способствует воссозданию наиболее экономичных опорных форм, тем самым значительно снижая весовой показатель металлических конструкций.
Балки разделяются по типу сечения,
они могут быть прокатными либо сварными
Двутавровая металлическая балка имеет ряд преимуществ. В первую очередь такой балкой можно перекрыть большие пролеты со значительной нагрузкой. Балка не горит (но надо помнить, что при воздействии высоких температур на балки – они теряют несущую способность). К тому же она устойчива к биологическому воздействию.
Использование двутавровых балок переменного сечения обеспечивает высокую эффективность внутреннего объема здания и значительно сокращают эксплуатационные расходы.
К недостаткам двутавровых сварных балок можно отнести:
1.Их подверженность коррозии, в случае отсутствия защитного покрытия и при наличии в здании агрессивных веществ;
2.Сложность установки – невозможна без применения специальной техники;
3.Необходимость расчета
для точного соответствия
В соответствии с вышесказанным определена тема курсового проекта «Расчет и проектирование двутавровой балки».
Цель:
Спроектировать двухтавровую балку для заданных условий работы и описать проблемы, связанные с технологией её изготовления.
Задачи:
1.Изучить информацию по курсовому проекту (используя различную литературу).
2.Выполнить расчеты по
определению элементов
3.Описать технологию
-способ сварки;
-выбрать режимы сварки;
-сварочные материалы;
-сварочное оборудование;
-описать последовательность изготовления;
4.Выполнить сборочный чертеж балки.
5.Сделать вывод.
1 ОСНОВНЯ ЧАСТЬ
1.1Технологическая часть
1.1.1 Описание конструкции
Двутавровая балка — это профиль конструктивных элементов, выполненный из черного металла. Имеет сечение, больше всего напоминающее букву «Н».
Для возведения сооружений ее начали использовать еще в начале двадцатого века. Двутавровая балка незаменима в современном строительстве. Она служит составляющей несущей конструкции. Основными свойствами, которым двутавр обязан такой популярностью, являются простая конструкция и особая прочность, выдерживающая большие нагрузки.
Двутавровая балка работает в несущих конструкциях преимущественно на изгиб. Сечение, присущее двутавру, признано самым выгодным и надежным, так как именно при этой конструкции лучше всего происходит распределение материала. Балка двутаврового профиля является в семь раз более прочной и в тридцать раз более жесткой, чем балка квадратного профиля равнозначной площади сечения.
Для производства балки применяют углеродистую и низколегированную стали. Длина изготовления балки двутавровой (двутавры) зависит от ее назначения. Этот вид металлопроката нашел свое применение в сферах промышленного и гражданского строительства, а также в производстве перекрытий, мостовых сооружений и т.д.
1.1.2 Выбор материала конструкции
Основной материал, из которого изготовлена балка – углеродистая, конструкционная сталь марки Ст 3 ГОСТ 380-94.
Сталь сваривается без ограничений всеми способами сварки, не склонна к трещинообразованию.
Сталь поставляется в виде листов или сортового проката.
Таблица 1 – Химический состав стали Ст 3 по ГОСТ 380-94, %:
Марка | Содержание элементов, % | ||||||||
C | Si | Mn | Cr | Ni | Cu | P | S | As | |
Ст 3 | 0,14-0,22 | 0,12-0,30 | 0,40-0,65 | ≤ 0,3 | ≤ 0,3 | ≤ 0,3 | 0,04 | 0,05 | 0,08 |
Механические свойства стали Ст 3 по ГОСТ 380-94:
- предел текучести σТ = 250 МПа;
- предел прочности σТ = 380-490 МПа;
- относительное удлинение δ = 26 %;
Оценка склонности основного металла к образованию трещин проводим по эквиваленту углерода:
Т.к. эквивалент углерода Сэ< 0,45, то делаем вывод, что сталь Ст 3 не склонна к образованию трещин и относится к хорошо свариваемым.
1.1.3 Выбор способа сварки
Выбор способа сварки зависит от многих факторов: от толщины металла, от марки материала, от сложности выполнения сварного шва, от условий работы конструкции, от длины шва, от типа производства.
Для длины 12м. рекомендуется использовать полуавтоматическую и автоматическую сварку под слоем флюса.
Также виды сварки как ручная дуговая сварка, и полуавтоматическая в среде защитного газа, контактная сварка – неприменимы, т.к. не обеспечивают требуемую глубину проплавления.
Выбор способа сварки от марки материала.
Для данной стали применимы все способы сварки.
Выбор способа сварки от сложности выполнения св. шва.
Шов открытого типа, поэтому применимы все способы сварки.
Выбор способа сварки от длины шва.
Длина двутавровой балки 12 м, поэтому лучше применять автоматическую сварку.
Выбор способа сварки от условий работы.
Балка эксплуатируется в условиях нормальных температур, при допустимой влажности воздуха. Сварку можно производить всеми способами.
Из предложенных выше способов можно предложить: автоматическую сварку под слоем флюса или автоматическую в среде защитного газа.
Наиболее лучшим способом сварки является под слоем флюса, т.к. флюс по сравнению с двуокисью углерода обеспечивает высокое качество сварного шва при минимальных затратах вспомогательных материалов.
1.1.4 Выбор сварочных материалов
Сварочные материалы должны обеспечивать механические свойства наплавленного металла шва не ниже механических свойств основного металла.
При автоматической сварке под слоем флюса применим сварочную проволоку марки Св08А ГОСТ 2246-70 диаметром 3 мм.
Химический состав сварочной проволоки Св08А ГОСТ 2246-70 приведен в таблице 2.
Таблица 2 — Химический состав проволоки Св08А, %
Углерод | Марганец | Кремний | Фосфор | Сера | Хром | Никель | Алюминий |
≤ 0,10 | 0,35 –0,6 | ≤0,03 | ≤0,03 | ≤0,03 | ≤0,12 | ≤0,25 | ≤0,01 |
Сварочный флюс марки АН-348А ГОСТ 9087-81. Область применения этого флюса – сварка и наплавка конструкций из низко углеродистых и низколегированных сталей, нелегированной и низколегированной сварочной проволокой при температурной эксплуатации конструкции до минус 50°С.
Химический состав флюса АН-348А ГОСТ 9087-81 приведен в таблице 2.
Таблица 3 – Химический состав флюсаАН-348А, %
SiO2 | CaO | MnO | Al2O3 | MgO | CaF2 | Fe2O3 | Сера | Фосфор | |
40-44 | ≤ 12 | 31-38 | ≤ 6 | <7 | 3-6 | не более | |||
0,5-2 | 0,12 | 0,12 | |||||||
Прихватки выполняются ручной дуговой сваркой, применяются электроды типа Э-50А УОНИ-13/55 ГОСТ 9466-75, диаметром 4 мм.
Требования к сварочным материалам:
Сварочные материалы перед использованием должны быть проконтролированы на наличие сертификата (на электроды, проволоку и флюс) с проверкой полноты приведенных в нем данных и их соответствия требованиям стандарта, технических условий или паспорта на конкретные сварочные материалы. Все сварочные материалы проверяются на отсутствие повреждений упаковок и самих материалов.
1.1.5 Технология
изготовления и монтажа
Последовательность операций выбирается с учетом возможностей сборочно-сварочного оборудования, транспортных средств и должна обеспечить качественное сварное соединение.
1. Транспортирование
Для сборки балки все сборочные единицы транспортируются к месту сборки. Для перемещения используют мостовой кран и захват.
2. Контроль
Проверка маркировки и сертификата листового проката.
Контроль деталей на соответствие требованиям чертежа (использовать штангенциркуль, рулетка).
3. Сборка
Двутавровая балка составляется из трех длинных листовых элементов (поясов и стенки).
Сборка деталей производится в сборочном кондукторе.
Кондуктор с винтовыми прижимами для сборки двутавровых балок. Основание выполнено в виде жесткой сварной рамной конструкции, состоящей из продольных и поперечных балок. Упоры и прижимы установлены на поперечных балках, продольные балки заделаны в фундамент. Подача длинных и гибких элементов балки в кондуктор осуществляется мостовым краном сверху с помощью жесткой траверсы со специальными захватами. Вертикальная стенка укладывается на продольные швеллеры, после чего устанавливаются полки, и детали плотно прижимаются друг к другу винтами. Прихватки обычно становятся только с одной стороны сверху, их размеры и расположение должны обеспечить жесткость и прочность балки при извлечении из приспособления краном и переносе к месту сварки.
Полный расчет балки на прочность и жесткость
Задача
Произвести полный расчет на прочность и проверить жесткость статически определимой двутавровой двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [σ]=160 МПа и [τ]=100 МПа, допустимый прогиб балки [f]=l/400
Рис. 1
Решение
Подготовка расчетной схемы к решению задачи:
Определение опорных реакций
Подробно, пример определения опорных реакций для балки рассмотрен здесь
А также в нашем коротком видеоуроке:
Из Σmв=0
Из ΣmА=0
Построение эпюр Q и М
Подробный пример построения эпюр поперечных сил Q и изгибающих моментов M для балки
Видео про расчет значений Q и M для построения эпюр:
В пролете балки 0 ≤ z2 ≤ l
QII= — RB+ qz2= -52+30∙z2QII(z=0)= -52 кН
QII(z=l)= -52+30∙4=68 кН
MII=RB∙z2-qz22/2=52z2-30∙z22/2
MII (z=0)= 0
MII (z=l)= -32 кНм
На консоли l ≤ z1≤ (l+a)
QI= — RB+ ql — RA=-52+30∙4-108=-40 кНMI=RB z1-ql(z1-l/2)+RA(z1-l)=52z1-30∙4(z1-4/2)+108(z1-4)
MI (z=l)= -32 кНм
MI (z=l+a)= 0
По этим данным построены эпюры Q и М.
Короткое видео о том, как надо строить эпюры:
Так как Мmах = 45 кНм, то
Wx≥Mmax / [σ] = 45∙103 / 160∙106= 0,281 м3= 281 см3.
О том, как подбирается сечение балки
По сортаменту выбираем двутавр № 24, для которого Wx = 289 см3, Ix= 3460 см4, Smax = 163 см3, h = 24 см, bп = 11,5 см, t = 0,95 см, d = bc = 0,56 см, h0 = h-2t = 22,1 см.
Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.
σmax = Mmax / Wx = 45∙103 / 289∙10-6= 156∙106 Па = 156 МПа
Проверка сечения балки по касательным напряжениям
Так как Qmax = 68 кН, то
Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:
Построение эпюры нормальных напряжений
Построение эпюры касательных напряжений
В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:
М = -32 кНм и Q = 68 кН.
Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1
Таблица 1
Результаты расчета в примере
Проверка прочности балки по главным напряжениям
Наиболее опасной точкой в неблагоприятном сечении является точка 3. В этой точке σ1=118 МПа и σ3= -16 МПа. Проверяем прочность в этой точке по третьей гипотезе прочности согласно неравенству σ1 — σ3≤ [σ].
Так как 118 — ( -16) = 134 < 160, то выбранное сечение удовлетворяет условию прочности и по главным напряжениям.
Расчет перемещений сечений (прогибов балки)
Универсальные уравнения МНП для сечения z:
Опорные условия:
1) при z=0: y(z)=0, следовательно, y0=0
2) при z=l: y(z)=0 находим θ0
откуда θ0= -8,48∙10-3 радиан.
Прогиб в пролете при z=l/2=4/2=2 м.
Аналогично определяется прогиб на конце консоли при z = l + a =4+0,8 = 4,8 м.
Проверка жесткости балки
— пролетной части:
yc=0,98 см < 1/400 = 400/400 = 1 см
— консольной части:
yD=0,33 см < 2a/400 = 2∙80/400 = 0,4 см.
Следовательно, принятая двутавровая балка удовлетворяет требуемому условию жесткости.
Другие примеры решения задач >

а – план перекрытия; б – расчетная схема главной балки; в – сечение балки;
1 – грузовая площадь
Цель: Проверка режима расчета сопротивления сечений в постпроцессоре «Сталь» вычислительного комплекса SCAD
Задача: Проверить расчетное сечение сварного двутаврового профиля для главных балок пролетом 18 м в балочной клетке нормального типа. Верхний пояс главных балок раскреплен второстепенными балками, расположенными с шагом 1,0 м.
Источник: Металлические конструкции: учебник для студ. Учреждений высш. проф. Образования / [Ю. И. Кудишин, Е. И. Беленя, В. С. Игнатьева и др.]; под. Ред. Ю. И. Кудишина. — 13-е изд., испр. — М. : Издательский центр «Академия», 2011. С 192.
Соответствие нормативным документам: СНиП II-23-81*, СП 16.13330, ДБН В.2.6-163:2010.
Имя файла с исходными данными:
4.5 SectionResistance_Example_4.5.spr;
отчет — 4.5 SectionResistance _Example_4.5.doc
Исходные данные:
| Ry = 23 кН/cм2, Rs = 0,58*23=13,3 кН/cм2 | Сталь марки C255 при толщине t>20 мм; |
| M = 6245 кНм | Расчетный изгибающий момент; |
| γc = 1 | Коэффициент условий работы; |
| l = 18 м | Пролет балки; |
| Iy = 2308077,083см4 | Геометрические характеристики для сварного |
| Wy = 27153,848см3 iy = 70,605см, iz = 11,577 см. | двутавра со стенкой 1650×12 мм и полками 530×25 мм; |
Результаты SCAD Постпроцессор СТАЛЬ:
[Элемент № 1] Усилия
N Макс. 0 Т | My Макс. 0 Т*м | Mz Макс. 0 Т*м |
Mk Макс. 0 Т*м | Qz Макс. 35,37 Т
| Qy Макс. 0 Т |
| Длина стержня 18 м |
|
Расчет выполнен по СНиП II-23-81*
Конструктивный элемент section
Сталь: C255
Длина элемента 18 м
Предельная гибкость для сжатых элементов: 250
Предельная гибкость для растянутых элементов: 250
Коэффициент условий работы 1
Коэффициент надежности по ответственности 1
Коэффициент расчетной длины XoZ — 1
Коэффициент расчетной длины XoY — 1
Расстояние между точками раскрепления на плоскости 1,125 м
Сечение

Результаты расчета | Проверка | Коэффициент использования |
|---|---|---|
п.5.12 | Прочность при действии изгибающего момента My | 1 |
пп.5.12,5.18 | Прочность при действии поперечной силы Qz | 0,14 |
пп.5.24,5.25 | Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики | 1 |
п.5.15 | Устойчивость плоской формы изгиба | 1 |
пп.6.15,6.16 | Предельная гибкость в плоскости XoY | 0,62 |
пп.6.15,6.16 | Предельная гибкость в плоскости XoZ | 0,1 |
Коэффициент использования 1 — Прочность при действии изгибающего момента My
Ручной расчет (СНиП II-23-81*):
1. Необходимый момент сопротивления балки:
\[ W_{nes} =\frac{M_{\max } }{R_{y} \gamma_{c} }=\frac{\mbox{6245}\cdot 100}{23}=27152,174 \quad см^{3}. \]
2. Гибкость элемента в плоскости и из плоскости действия момента:
\[ \lambda_{y} =\frac{\mu l}{i_{y} }=\frac{18,0\cdot 100}{70,605}=25,4939; \] \[ \lambda_{z} =\frac{\mu l}{i_{z} }=\frac{18,0\cdot 100}{11,577}=155,481. \]
Сравнение решений:
Фактор | Источник | Ручной счет | SCAD | Отклонение от ручного счета, % |
|---|---|---|---|---|
Прочность при действии изгибающего момента Му | 1,0 | 27152,174/27153,848 = 1,0 | 1,0 | 0,0 |
Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики | – | 27152,174/27153,848 = 1,0 | 1,0 | 0,0 |
Устойчивость плоской формы изгиба | – | 27152,174/1/27153,848 = 1,0 | 1,0 | 0,0 |
Предельная гибкость в плоскости XoZ | – | 25,4939/250 = 0,102 | 0,102 | 0,0 |
Предельная гибкость в плоскости XoY | – | 155,481/250 = 0,622 | 0,622 | 0,0 |
Комментарии:
- Проверка прочности балки с учетом развития ограниченных пластических деформаций не выпонялась, поскольку согласно норм такой рачет возможен только при соответствующем оребрении стенки балки. В исходных данных примера балка настила задавалась без промежуточных ребер жесткости.
- Проверка устойчивости плоской формы изгиба при автоматизированном расчете выполнялась согласно норм при φb = 1,0 для расчетной длины lef = 1м.
| Конфигурация сварного шва | Примечания: для калькуляторов требуется премиум-членство |
 | Методы оценки проектирования сварочных конструкций — для просмотра документа | требуется премиум-членство
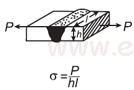 | Осевая нагрузка Полное проникновение Сварка, равная напряжению толщины пластины. Open: Калькулятор сварного шва с полным проникновением осевой нагрузки |
|---|---|
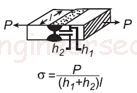 | Аксиальная нормальная нагрузка Частичное проникновение Уравнение напряжения толщины сварного шва и калькулятор. Open: калькулятор сварного шва с частичным проникновением при нормальной нагрузке |
 | Тройник нагрузки нагрузки полного проникновения сварного напряжения уравнения и калькулятор. Open: Тройник нагрузки нагрузки полного проникновения сварки калькулятор напряжения |
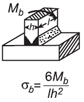 | Тройник. Сечение нагрузки при полном проникновении Сварочный момент. Open: Тройное сечение нагрузки Проникновение сварного шва Момент нагрузки Прикладное напряжение Калькулятор |
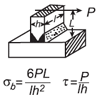 | Тройник сечение нагрузки Проникновение сварного шва Перпендикулярная нагрузка Калькулятор приложенного напряжения. Open: Тройник нагрузки на шов при полном проникновении Перпендикулярная нагрузка Калькулятор приложенного напряжения |
 | Сварка изгибающего момента при сварке встык. Сварочное напряжение. Open: Сварочный момент сварного шва Нагрузка на полное проникновение Сварка Напряжение Напряжение Калькулятор напряжения. |
 | Частичное проникновение изгиба сварного шва Напряжение сварки. Open: Калькулятор напряжения сварного шва при частичном проникновении. |
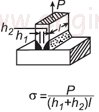 | Тройник. Частичная нагрузка Сварочный шов Перпендикулярная нагрузка Калькулятор приложенного напряжения. Open: Тройник. Частичная нагрузка Сварочный шов Перпендикулярная нагрузка Калькулятор приложенного напряжения |
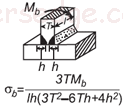 | Тройник Раздел Частичное проникновение Сварочный момент изгиба сварного шва Калькулятор приложенного напряжения Открыть: Тройное сечение Нагруженное частичное проникновение Сварочный момент Прикладное напряжение Калькулятор |
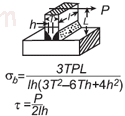 | Напряжение, созданное для частичного сварного напряжения перпендикулярности сварного шва. Open: Напряжение, созданное для напряжения сварки с частичной перпендикулярностью сварного шва. |
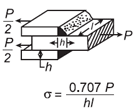 | Напряжение, создаваемое для сварного шва конфигурации с тремя пластинами, равно толщине пластины. Open: Напряжение, создаваемое для сварного шва с конфигурацией соединения трех пластин, равно толщине пластины. |
 | Калькулятор напряжения сварного шва с осевой нагрузкой с двумя пластинами Open: калькулятор напряжений при сварке с осевой нагрузкой с двумя пластинами |
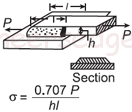 | Напряжение, созданное для конфигурации параллельной сварки двух пластин. Open: Создано напряжение для калькулятора конфигурации параллельной сварки двух пластин. |
 | Напряжение, созданное для конфигурации двух перпендикулярных сварных швов. Open: Напряжение создано для калькулятора конфигурации перпендикулярной сварки двух пластин. |
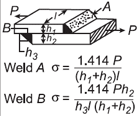 | Напряжение, созданное для конфигурации перпендикулярного шва внахлестку. Open: Калькулятор конфигурации перпендикулярного сварного шва на пластине под напряжением. |
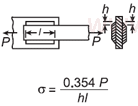 | Уравнение и калькулятор напряжений параллельной сварки с осевой нагрузкой с тремя коленками Open: Калькулятор напряжений при параллельной сварке с трехсторонним сварочным швом |
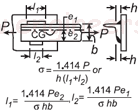 | Пластина «L» Раздел Калькулятор сварочного напряжения Open: Лист «L» Калькулятор напряжения сварного шва |
 | Напряжение сдвига при сварке для приложенного крутящего момента в уравнениях и валу твердого вала Open: Напряжение сдвига при сварке для приложенного крутящего момента на калькуляторе с твердым валом |
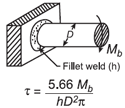 | Напряжение сдвига при сварке для приложенного изгибающего момента на уравнении сплошного вала и калькуляторе Open: Напряжение сдвига при сварке для приложенного изгибающего момента на калькуляторе с твердым валом |
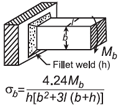 | Напряжение сдвига сварного шва для прикладного изгибающего момента на уравнение прямоугольника / квадратного вала и калькулятор Open: Напряжение сдвига при сварке для прикладного изгибающего момента на калькуляторе прямоугольной формы / квадратного вала |
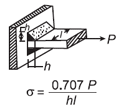 | Напряжение сдвига при сварке для прикладного изгибающего момента на уравнении луча прямоугольника и калькуляторе Open: Напряжение сдвига при сварке для прикладного изгибающего момента на калькуляторе луча прямоугольника |
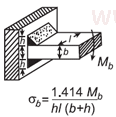 | Напряжение сдвига при сварке для прикладного изгибающего момента на уравнении луча прямоугольника и калькуляторе Open: Напряжение сдвига при сварке для прикладного изгибающего момента на калькуляторе луча прямоугольника |
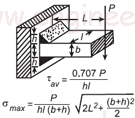 | Напряжение сдвига при сварке для приложенного изгибающего усилия на уравнении луча прямоугольника и калькуляторе Open: Напряжение сдвига при сварке для приложенного изгибающего усилия на калькуляторе луча прямоугольника |
 | Напряжение сварки для изгибающего момента Прикладное прямоугольное уравнение и калькулятор Open: Напряжение сварки при изгибающем моменте Прикладной прямоугольный калькулятор пучка |
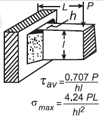 | Напряжение сварки при нагрузке, приложенной к уравнению и калькулятору прямоугольного сечения. Open: Сварочное напряжение для нагрузки, приложенной к калькулятору прямоугольного сечения. |
 | Напряжение сварки на момент, приложенное к уравнению и калькулятору прямоугольного сечения. Open: Сварочное напряжение на момент, приложенное к калькулятору прямоугольного сечения |
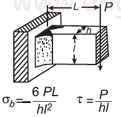 | Напряжение сварки для нагрузки, приложенной к уравнению и калькулятору прямоугольного сечения Open: Сварочное напряжение для нагрузки, приложенной к калькулятору прямоугольного сечения |
 | Напряжение сварки на момент, приложенное к уравнению и калькулятору прямоугольного сечения. Сварочное напряжение на момент, приложенное к прямоугольному калькулятору луча. |
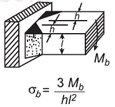 | Напряжение сварки на момент, приложенное к уравнению и калькулятору прямоугольного сечения. Open: Сварочное напряжение на момент, приложенное к прямоугольному калькулятору луча. |
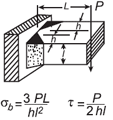 | Напряжение сварки для нагрузки, приложенной к уравнению и калькулятору прямоугольного сечения Open: Сварочное напряжение для нагрузки, приложенной к калькулятору прямоугольного сечения |
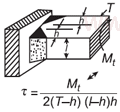 | Напряжение сварки для изгибающего момента, приложенное к уравнению и калькулятору прямоугольного сечения Open: Напряжение сварки для изгибающего момента, приложенное к калькулятору прямоугольного сечения |
 | Напряжение сварки для уравнения и калькулятора пучка сращивания Open: Сварочное напряжение для калькулятора луча сращивания |
 | Расчет сварных швов калькулятора электронных таблиц балок |
 | Калькулятор электронных таблиц Lifting Lug Design |
 | Калькулятор массы и площади сварного шва Расчет калькулятора для удвоенного V, одинарного V, соединения V, подложки и массы и площади сварного шва J. |
 | Weld Branch ASME B31.3 Электронная таблица Excel Calculator
|
% PDF-1.4 % 198 0 объектов > endobj Xref 198 114 0000000016 00000 n 0000003293 00000 n 0000003497 00000 n 0000003524 00000 n 0000003582 00000 n 0000003618 00000 n 0000004037 00000 n 0000004155 00000 n 0000004272 00000 n 0000004390 00000 n 0000004508 00000 n 0000004626 00000 n 0000004747 00000 n 0000004868 00000 n 0000004989 00000 n 0000005110 00000 n 0000005250 00000 n 0000005369 00000 n 0000005489 00000 n 0000005609 00000 n 0000005729 00000 n 0000005850 00000 n 0000005969 00000 n 0000006090 00000 n 0000006210 00000 n 0000006367 00000 n 0000006447 00000 n 0000006527 00000 n 0000006608 00000 n 0000006688 00000 n 0000006768 00000 n 0000006847 00000 n 0000006926 00000 n 0000007006 00000 n 0000007084 00000 n 0000007164 00000 n 0000007243 00000 n 0000007323 00000 n 0000007401 00000 n 0000007479 00000 n 0000007556 00000 n 0000007637 00000 n 0000007855 00000 n 0000008402 00000 n 0000008860 00000 n 0000009466 00000 n 0000009953 00000 n 0000010284 00000 n 0000010445 00000 n 0000011176 00000 n 0000011616 00000 n 0000011680 00000 n 0000011970 00000 n 0000012179 00000 n 0000016584 00000 n 0000016991 00000 n 0000017396 00000 n 0000017674 00000 n 0000021329 00000 n 0000021664 00000 n 0000022052 00000 n 0000022251 00000 n 0000028663 00000 n 0000029206 00000 n 0000029598 00000 n 0000030009 00000 n 0000030087 00000 n 0000032386 00000 n 0000032705 00000 n 0000033078 00000 n 0000033257 00000 n 0000034035 00000 n 0000034238 00000 n 0000034725 00000 n 0000035072 00000 n 0000039288 00000 n 0000039650 00000 n 0000040306 00000 n 0000041019 00000 n 0000041716 00000 n 0000042365 00000 n 0000043188 00000 n 0000043434 00000 n 0000043765 00000 n 0000043892 00000 n 0000044907 00000 n 0000045655 00000 n 0000046394 00000 n 0000046948 00000 n 0000080179 00000 n 0000094753 00000 n 0000096636 00000 n 0000096904 00000 n 0000097255 00000 n 0000097387 00000 n 0000097944 00000 n 0000098153 00000 n 0000098444 00000 n 0000098508 00000 n 0000098566 00000 n 0000098781 00000 n 0000098874 00000 n 0000098965 00000 n 0000099074 00000 n 0000099174 00000 n 0000099324 00000 n 0000099439 00000 n 0000099553 00000 n 0000099703 00000 n 0000099802 00000 n 0000099901 00000 n 0000100013 00000 n 0000100139 00000 n 0000002576 00000 n прицеп ] >> startxref 0 %% EOF 311 0 объектов > поток xb«`f` ̀
.Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{}} L10n_strings.COLLECTION_DESCRIPTION {{AddToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ Пункт}} {{}} l10n_strings.PRODUCTS {{}} L10n_strings.DRAG_TEXT{{l10n_strings.DRAG_TEXT_HELP}}
{{}} L10n_strings.LANGUAGE {{$ Select.selected.display}}{{статья.content_lang.display}}
{{}} L10n_strings.AUTHOR{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ Выбора.selected.display}} {{}} L10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON {{}} L10n_strings.CREATE_A_COLLECTION_ERROR ,
,нагрузок на балки — Калькулятор силы опоры

Онлайн-калькулятор силы поддержки балки
Приведенный ниже калькулятор можно использовать для расчета сил поддержки — R 1 и R 2 — для балок до 6 асимметричных нагрузок.
Длина балки (м, футы)
Сила F1 (N, фунт f ) Расстояние от R 1 (м, фут)
Сила F2 (N, фунт ) f ) расстояние от R 1 (м, футы)
сила F3 (N, фунт f ) расстояние от R 1 (м, футы)
сила F4 ( N, фунт f ) расстояние от R 1 (м, фут)
Сила F5 (N, фунт f ) расстояние от R 1 (м, фут)
Сила F6 (N, фунт f ) Расстояние от R 1 (м, фут)
Для балансира, нагруженного весами (или другими нагрузками), силы реакции — R — на опорах равно сил нагрузки — F . Силовой баланс можно выразить как
F 1 + F 2 + …. + F n = R 1 + R 2 (1)
где
F = сила от нагрузки (N, фунт f )
R = сила от опоры (N, фунт f )
Дополнительно к балансу в балансе алгебраическая сумма моментов равен нулю .Моментный баланс можно выразить как
F 1 a f1 + F 2 a f2 + …. + F n a фн = R a r1 + R a r2 (2)
, где
a = расстояние от силы до общего задания — обычно расстояние до одной из опор (м, футы)
Пример — A балка с двумя симметричными нагрузками
длиной 10 м и длиной балка с двумя опорами нагружены двумя равными и симметричными нагрузками F 1 и F 2 , каждая 500 кг .Силы поддержки F 3 и F 4 можно рассчитать
(500 кг) (9,81 м / с 2 ) + (500 кг) (9,81 м / с 2 ) = R 1 + R 2
=>
R 1 + R 2 = 9810 N
= 9,8 кН
Примечание! Нагрузка из-за массы — м. — мг. Ньютона — где г = 9.81 м / с 2 .
При симметричных и одинаковых нагрузках опорные силы также будут симметричными и равными. Используя
R 1 = R 2
, приведенное выше уравнение можно упростить до
R 1 = R 2 = (9810 Н) / 2
= 4905 N
= 4,9 кН
Связанные мобильные приложения от Engineering ToolBox 
— бесплатные приложения для автономного использования на мобильных устройствах.
Пример. Балка с двумя несимметричными нагрузками.
Балка длиной м длиной 1001 с двумя опорами нагружена двумя нагрузками, 500 кг расположена на расстоянии 1 м от конца ( R 1 ). , а другая нагрузка на 1000 кг находится на на 6 м с того же конца. Баланс сил можно выразить как
(500 кг) (9,81 м / с 2 ) + (1000 кг) (9,81 м / с 2 ) = R 1 + R 2
=>
R 1 + R 2 = 14715 N
= 14.7 кН
Алгебраическая сумма моментов (2) может быть выражена как
(500 кг) (9,81 м / с 2 ) (1 м) + (1000 кг) (9,81 м / с 2 ) (6 м) =? R 1 (0 м) + R 2 (10 м)
=>
R 2 = 6377 (N)
= 6,4 кН
F 3 можно рассчитать как:
R 1 = (14715 N) — (6377 N)
= 8338 N
= 8.3 кН
Вставьте балки в модель Sketchup с помощью Extension Sketchup Engineering ToolBox












