Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Отрезки и прямые, связанные с окружностью

Фигура	Рисунок	Определение и свойства
Окружность		Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Круг		Конечная часть плоскости, ограниченная окружностью
Радиус		Отрезок, соединяющий центр окружности с любой точкой окружности
Хорда		Отрезок, соединяющий две любые точки окружности
Диаметр		Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности
Касательная		Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания
Секущая		Прямая, пересекающая окружность в двух точках

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Фигура	Рисунок	Теорема
Пересекающиеся хорды		Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство
Касательные, проведённые к окружности из одной точки		Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство
Касательная и секущая, проведённые к окружности из одной точки		Справедливо равенство Посмотреть доказательство
Секущие, проведённые из одной точки вне круга		Справедливо равенство: Посмотреть доказательство

Пересекающиеся хорды
	Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство
Касательные, проведённые к окружности из одной точки
	Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство
Касательная и секущая, проведённые к окружности из одной точки
	Справедливо равенство Посмотреть доказательство
Секущие, проведённые из одной точки вне круга
	Справедливо равенство: Посмотреть доказательство

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство

Касательная и секущая, проведённые к окружности из одной точки

Справедливо равенство Посмотреть доказательство

Секущие, проведённые из одной точки вне круга

Справедливо равенство: Посмотреть доказательство

Доказательства теорем о длинах хорд, касательных и секущих

      Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Рис. 1

      Тогда справедливо равенство

      Доказательство. Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

      Теорема 2 . Предположим, что из точки A, лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Рис. 2

      Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

      Доказательство. Заметим, что угол ABC образован касательной AB и хордой BC, проходящей через точку касания B. Поэтому величина угла ABC равна половине угловой величины дуги BC. Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC. Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

      Теорема 3 . Предположим, что из точки A, лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Рис. 3

      Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

      Доказательство. Проведём из точки A касательную AB к окружности (рис. 4).

Рис. 4

      Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

      Теорема о бабочке. Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Рис. 5

      Доказательство. Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B. Теперь введём следующие обозначения:

      Воспользовавшись теоремой синусов, применённой к треугольнику CKG, получим

(1)

Воспользовавшись теоремой синусов, применённой к треугольнику AKG, получим

(2)

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Поэтому

      Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL, получим равенство

откуда вытекает равенство

x = y ,

что и завершает доказательство теоремы о бабочке.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Хорда (геометрия) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Хорда. 1 — секущая, 2 — хорда AB (отмечена красным цветом), 3 — сегмент (отмечен зелёным цветом), 4 — дуга

Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы).

Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. Плоская фигура, заключённая между кривой и её хордой называется сегментом, а часть кривой, находящаяся между двумя крайними точками хорды называется дугой. В случае с замкнутыми кривыми (например, окружностью, эллипсом) хорда образует пару дуг с одними и теми же крайними точками по разные стороны хорды. Хорда, проходящая через центр окружности, является её диаметром. Диаметр — самая длинная хорда в окружности.

Хорда и расстояние до центра окружности[править | править код]

• Если расстояния от центра окружности до хорд равны, то эти хорды равны.
• Если хорды равны, то расстояния от центра окружности до этих хорд равны.
• Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше.
• Если расстояние от центра окружности до хорды меньше, то эта хорда больше. Если расстояние от центра окружности до хорды больше, то эта хорда меньше.
• Наибольшая возможная хорда является диаметром.
• Наименьшая возможная хорда является точкой.
• Если хорда проходит через центр окружности, то эта хорда является диаметром.
• Если расстояние от центра окружности до хорды равно радиусу, то эта хорда является точкой.
• Серединный перпендикуляр к хорде проходит через центр окружности.

Хорда и диаметр[править | править код]

• Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде.
• Если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам.
• Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам.
• Если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу.
• Если диаметр перпендикулярен хорде, то этот диаметр делит дуги, стягиваемые этой хордой, пополам.
• Если диаметр делит дугу пополам, то этот диаметр перпендикулярен хорде, стягивающей эту дугу.

Хорда и радиус[править | править код]

• Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде.
• Если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам.
• Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам.
• Если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
• Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам.
• Если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.

Хорда и вписанный угол[править | править код]

• Если вписанные углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то эти углы равны.
• Если пара вписанных углов опирается на одну и ту же хорду и вершины этих углов лежат по разные стороны этой хорды, то сумма этих углов равна 180°.
• Если вписанный и центральный углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то вписанный угол равен половине центрального угла.
• Если вписанный угол опирается на диаметр, то этот угол является прямым.

Хорда и центральный угол[править | править код]

• Если хорды стягивают равные центральные углы, то эти хорды равны.
• Если хорды равны, то эти хорды стягивают равные центральные углы.
• Большая хорда стягивает больший центральный угол, меньшая хорда стягивает меньший центральный угол.
• Больший центральный угол стягивается большей хордой, меньший центральный угол стягивается меньшей хордой.

Хорда и дуга[править | править код]

• Если хорды стягивают равные дуги, то эти хорды равны.
• Если хорды равны, то эти хорды стягивают равные дуги.
• Из дуг, меньших полуокружности, большая дуга стягивается большей хордой, меньшая дуга стягивается меньшей хордой.
• Из дуг, меньших полуокружности, большая хорда стягивает большую дугу, меньшая хорда стягивает меньшую дугу.
• Из дуг, больших полуокружности, меньшая дуга стягивается большей хордой, большая дуга стягивается меньшей хордой.
• Из дуг, больших полуокружности, большая хорда стягивает меньшую дугу, меньшая хорда стягивает большую дугу.
• Хорда, стягивающая полуокружность, является диаметром.
• Если хорды параллельны, то дуги, заключённые между этими хордами (не путать с дугами, стягиваемыми хордами), равны.

Другие свойства[править | править код]

Рис. 1. AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}

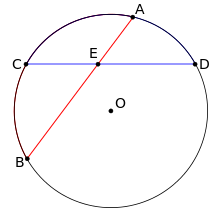
• При пересечении двух хорд AB и CD в точке E получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. рис. 1): AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}.
• Если хорда делится пополам какой-либо точкой, то её длина самая маленькая по сравнению с длинами проведённых через эту точку хорд.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Вписанные и центральные углы

      Определение 1. Центральным угломназывают угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Рис. 1

      Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Рис. 2

      Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

      Определение 3. Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.

Теоремы о вписанных и центральных углах

Фигура	Рисунок	Теорема
Вписанный угол		Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
Вписанный угол		Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды
Вписанный угол		Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
Окружность, описанная около прямоугольного треугольника		Середина гипотенузы прямоугольного треугольника является центром описанной около этого треугольника окружности. Посмотреть доказательство

Вписанный угол

Теорема: Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство

Теорема: Вписанные углы, опирающиеся на одну и ту же дугу равны.

Теорема: Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Теорема: Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды

Теорема: Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Окружность, описанная около прямоугольного треугольника

Теорема: Середина гипотенузы прямоугольного треугольника является центром описанной около этого треугольника окружности. Посмотреть доказательство

Теоремы об углах, образованных хордами, касательными и секущими

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами		Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство
Угол, образованный секущими, которые пересекаются вне круга		Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство
Угол, образованный касательной и хордой, проходящей через точку касания		Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство
Угол, образованный касательной и секущей		Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство
Угол, образованный двумя касательными к окружности		Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство

Угол, образованный пересекающимися хордами хордами

Формула:

Теорема Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство

Угол, образованный секущими секущими, которые пересекаются вне круга

Формула:

Теорема Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство

Угол, образованный касательной и хордой хордой, проходящей через точку касания

Формула:

Теорема Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство

Угол, образованный касательной и секущей касательной и секущей

Формула:

Теорема Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство

Угол, образованный двумя касательными касательными к окружности

Формулы:

Теорема Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство

Доказательства теорем об углах, связанных с окружностью

      Теорема 1. Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

      Доказательство. Рассмотрим сначала вписанный угол ABC, сторона BC которого является диаметром окружности диаметром окружности, и центральный угол AOC (рис. 5).

Рис. 5

      Так как отрезки AO и BO являются радиусами окружности радиусами окружности, то треугольник AOB – равнобедренный, и угол ABO равен углу OAB. Поскольку угол AOC является внешним углом треугольника AOB, то справедливы равенства

      Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

      Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

Рис. 6

      В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

      Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

Рис. 7

      В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

      Теорема 2. Величина угла, образованного пересекающимися хордами хордами, равна половине суммы величин дуг, заключённых между его сторонами.

      Доказательство. Рассмотрим рисунок 8.

Рис. 8

      Нас интересует величина угла AED, образованного пересекающимися в точке E хордами AB и CD. Поскольку угол AED – внешний угол треугольника BED, а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

      Теорема 3. Величина угла, образованного секущими секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

      Доказательство. Рассмотрим рисунок 9.

Рис. 9

      Нас интересует величина угла BED, образованного пересекающимися в точке E секущими AB и CD. Поскольку угол ADC – внешний угол треугольника ADE, а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

      Теорема 4. Величина угла, образованного касательной и хордой касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

      Доказательство. Рассмотрим рисунок 10.

Рис. 10

      Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр, проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

      Теорема 5. Величина угла, образованного касательной и секущей касательной и секущей, равна половине разности величин дуг, заключённых между сторонами этого угла.

      Доказательство. Рассмотрим рисунок 11.

Рис. 11

      Нас интересует величина угла BED, образованного касательной AB и секущей CD. Заметим, что угол BDC – внешний угол треугольника DBE, а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB, в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

      Теорема 6.Величина угла, образованного двумя касательными к окружности касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами.

      Доказательство. Рассмотрим рисунок 12.

Рис. 12

      Нас интересует величина угла BED, образованного касательными AB и CD. Заметим, что углы BOD и BED в сумме составляют   π радиан. Поэтому справедливо равенство

α = π – γ .

      Далее получаем

что и требовалось доказать.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Все что нужно знать об окружности

Эта статья содержит минимальный набор сведений об окружности, необходимый для успешной сдачи ЕГЭ по математике.

Окружностью называется множество точек, расположенных на одинаковом  расстоянии от данной точки, которая называется центром окружности.

Для любой точки

, лежащей на окружности выполняется равенство ( Длина отрезка равна радиусу окружности.

Отрезок, соединяющий две точки окружности называется хордой.

Хорда, проходящая через центр окружности называется диаметром окружности ().

Длина окружности:

Площадь круга:

Дуга окружности:

Часть окружности, заключенная между двумя ее точками называется дугой окружности. Две точки окружности определяют две дуги. Хорда  стягивает две дуги: и . Равные хорды стягивают равные дуги.

Угол между двумя радиусами называется центральным углом:

Чтобы найти длину дуги , составляем пропорцию:

а) угол дан в градусах:

Отсюда

б) угол дан в радианах:

Отсюда

Диаметр, перпендикулярный хорде, делит эту хорду и дуги, которые она стягивает пополам:

Если  хорды и окружности пересекаются в точке , то произведения отрезков хорд, на которые они делятся точкой равны между собой:

Касательная к окружности.

Прямая, имеющая с окружностью одну общую точку называется касательной к окружности. Прямая, имеющая с окружностью две общие точки называется секущей.

Касательная к окружности перпендикулярна радиусу, проведенному к  точке касания.

Если из данной точки  проведены к окружности две касательные, то отрезки касательных  равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке:

Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной  равен произведению  всего отрезка секущей на его внешнюю часть:

Следствие: произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть:

Углы в окружности.

Градусная мера центрального угла равна градусной мере дуги, на которую он опирается:

∠ ⌣

 

Угол, вершина которого лежит на окружности, а стороны содержат хорды, называется вписанным углом.  Вписанный угол измеряется половиной дуги, на которую он опирается:

∠∠

Вписанный угол, опирающийся на диаметр, прямой:

∠∠∠

Вписанные углы, опирающиеся на одну дугу, равны:

∠∠∠

 

Вписанные углы, опирающиеся на одну хорду равны или их сумма равна

∠∠

∠∠∠

Вершины треугольников с заданным основанием и равными углами при вершине лежат на одной окружности:

Угол между двумя хордами (угол с вершиной внутри окружности) равен полусумме угловых величин дуг окружности, заключенных внутри данного угла и внутри вертикального угла.

∠ ∠∠( ⌣ ⌣ )

Угол между двумя секущими (угол с вершиной вне окружности) равен полуразности угловых величин дуг окружности, заключенных внутри угла.

∠ ∠∠( ⌣ ⌣ )

 Вписанная окружность.

Окружность называется вписанной в многоугольник, если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

Не во всякий многоугольник можно вписать окружность.

Площадь многоугольника, в который вписана окружность можно найти по формуле

,

здесь — полупериметр многоугольника, — радиус вписанной окружности.

Отсюда радиус вписанной окружности равен

Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны. Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:

В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.

Радиус вписанной окружности равен . Здесь

Описанная окружность.

Окружность называется описанной около многоугольника, если она проходит через все вершины многоугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров сторон многоугольника. Радиус вычисляется как радиус окружности, описанной около треугольника, определенного любыми тремя вершинами данного многоугольника:

Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна .

∠+∠=∠+∠

Около любого треугольника можно описать окружность, притом только одну. Ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника:

Радиус описанной окружности вычисляется по формулам:

Где — длины сторон треугольника, — его площадь.

Теорема Птолемея

Во вписанном четырехугольнике произведение диагоналей равно сумме произведений его противоположных сторон:

Окружность. Основные теоремы

\[{\Large{\text{Центральные и вписанные углы}}}\]

Определения

Центральный угол – это угол, вершина которого лежит в центре окружности.

 

Вписанный угол – это угол, вершина которого лежит на окружности.

 

Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.

 

Теорема

Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

 

Доказательство

Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка \(B\) – вершина вписанного угла \(ABC\) и \(BC\) – диаметр окружности:

 

Треугольник \(AOB\) – равнобедренный, \(AO = OB\), \(\angle AOC\) – внешний, тогда \(\angle AOC = \angle OAB + \angle ABO = 2\angle ABC\), откуда \(\angle ABC = 0,5\cdot\angle AOC = 0,5\cdot\buildrel\smile\over{AC}\).

 

Теперь рассмотрим произвольный вписанный угол \(ABC\). Проведём диаметр окружности \(BD\) из вершины вписанного угла. Возможны два случая:

 

1) диаметр разрезал угол на два угла \(\angle ABD, \angle CBD\)(для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.

 

2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла \(\angle ABD, \angle CBD\), у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.

 

Следствия

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

 

2. Вписанный угол, опирающийся на полуокружность, прямой.

 

3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.  

\[{\Large{\text{Касательная к окружности}}}\]

Определения

Существует три типа взаимного расположения прямой и окружности:

 

1) прямая \(a\) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние \(d\) от центра окружности до прямой меньше радиуса \(R\) окружности (рис. 3).

 

2) прямая \(b\) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка \(B\) – точкой касания. В этом случае \(d=R\) (рис. 4).

 

3) прямая \(c\) не имеет общих точек с окружностью (рис. 5).

 

Теорема

1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

 

2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.

 

Следствие

Отрезки касательных, проведенных из одной точки к окружности, равны.

 

Доказательство

Проведем к окружности из точки \(K\) две касательные \(KA\) и \(KB\):

 

Значит, \(OA\perp KA, OB\perp KB\) как радиусы. Прямоугольные треугольники \(\triangle KAO\) и \(\triangle KBO\) равны по катету и гипотенузе, следовательно, \(KA=KB\).

 

Следствие

Центр окружности \(O\) лежит на биссектрисе угла \(AKB\), образованного двумя касательными, проведенными из одной точки \(K\).  

\[{\Large{\text{Теоремы, связанные с углами}}}\]

Теорема об угле между секущими

Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.

 

Доказательство

Пусть \(M\) – точка, из которой проведены две секущие как показано на рисунке:

 

Покажем, что \(\angle DMB = \dfrac{1}{2}(\buildrel\smile\over{BD} — \buildrel\smile\over{CA})\).

 

\(\angle DAB\) – внешний угол треугольника \(MAD\), тогда \(\angle DAB = \angle DMB + \angle MDA\), откуда \(\angle DMB = \angle DAB — \angle MDA\), но углы \(\angle DAB\) и \(\angle MDA\) – вписанные, тогда \(\angle DMB = \angle DAB — \angle MDA = \frac{1}{2}\buildrel\smile\over{BD} — \frac{1}{2}\buildrel\smile\over{CA} = \frac{1}{2}(\buildrel\smile\over{BD} — \buildrel\smile\over{CA})\), что и требовалось доказать.

 

Теорема об угле между пересекающимися хордами

Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: \[\angle CMD=\dfrac12\left(\buildrel\smile\over{AB}+\buildrel\smile\over{CD}\right)\]

Доказательство

\(\angle BMA = \angle CMD\) как вертикальные.

 

Из треугольника \(AMD\): \(\angle AMD = 180^\circ — \angle BDA — \angle CAD = 180^\circ — \frac12\buildrel\smile\over{AB} — \frac12\buildrel\smile\over{CD}\).

 

Но \(\angle AMD = 180^\circ — \angle CMD\), откуда заключаем, что \[\angle CMD = \frac12\cdot\buildrel\smile\over{AB} + \frac12\cdot\buildrel\smile\over{CD} = \frac12(\buildrel\smile\over{AB} + \buildrel\smile\over{CD}).\]

Теорема об угле между хордой и касательной

Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой.

 

Доказательство

Пусть прямая \(a\) касается окружности в точке \(A\), \(AB\) – хорда этой окружности, \(O\) – её центр. Пусть прямая, содержащая \(OB\), пересекает \(a\) в точке \(M\). Докажем, что \(\angle BAM = \frac12\cdot \buildrel\smile\over{AB}\).

 

Обозначим \(\angle OAB = \alpha\). Так как \(OA\) и \(OB\) – радиусы, то \(OA = OB\) и \(\angle OBA = \angle OAB = \alpha\). Таким образом, \(\buildrel\smile\over{AB} = \angle AOB = 180^\circ — 2\alpha = 2(90^\circ — \alpha)\).

Так как \(OA\) – радиус, проведённый в точку касания, то \(OA\perp a\), то есть \(\angle OAM = 90^\circ\), следовательно, \(\angle BAM = 90^\circ — \angle OAB = 90^\circ — \alpha = \frac12\cdot\buildrel\smile\over{AB}\).

 

Теорема о дугах, стягиваемых равными хордами

Равные хорды стягивают равные дуги, меньшие полуокружности.

 

И наоборот: равные дуги стягиваются равными хордами.

 

Доказательство

1) Пусть \(AB=CD\). Докажем, что меньшие полуокружности дуги \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\).

 

\(\triangle AOB=\triangle COD\) по трем сторонам, следовательно, \(\angle AOB=\angle COD\). Но т.к. \(\angle AOB, \angle COD\) — центральные углы, опирающиеся на дуги \(\buildrel\smile\over{AB}, \buildrel\smile\over{CD}\) соответственно, то \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\).

 

2) Если \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\), то \(\triangle AOB=\triangle COD\) по двум сторонам \(AO=BO=CO=DO\) и углу между ними \(\angle AOB=\angle COD\). Следовательно, и \(AB=CD\).

 

Теорема

Если радиус делит хорду пополам, то он ей перпендикулярен.

Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.

 

Доказательство

1) Пусть \(AN=NB\). Докажем, что \(OQ\perp AB\).

 

Рассмотрим \(\triangle AOB\): он равнобедренный, т.к. \(OA=OB\) – радиусы окружности. Т.к. \(ON\) – медиана, проведенная к основанию, то она также является и высотой, следовательно, \(ON\perp AB\).

 

2) Пусть \(OQ\perp AB\). Докажем, что \(AN=NB\).

 

Аналогично \(\triangle AOB\) – равнобедренный, \(ON\) – высота, следовательно, \(ON\) – медиана. Следовательно, \(AN=NB\).  

\[{\Large{\text{Теоремы, связанные с длинами отрезков}}}\]

Теорема о произведении отрезков хорд

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

 

Доказательство

Пусть хорды \(AB\) и \(CD\) пересекаются в точке \(E\).

Рассмотрим треугольники \(ADE\) и \(CBE\). В этих треугольниках углы \(1\) и \(2\) равны, так как они вписанные и опираются на одну и ту же дугу \(BD\), а углы \(3\) и \(4\) равны как вертикальные. Треугольники \(ADE\) и \(CBE\) подобны (по первому признаку подобия треугольников).

 

Тогда \(\dfrac{AE}{EC} = \dfrac{DE}{BE}\), откуда \(AE\cdot BE = CE\cdot DE\).

 

Теорема о касательной и секущей

Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.

 

Доказательство

Пусть касательная проходит через точку \(M\) и касается окружности в точке \(A\). Пусть секущая проходит через точку \(M\) и пересекает окружность в точках \(B\) и \(C\) так что \(MB < MC\). Покажем, что \(MB\cdot MC = MA^2\).

 

Рассмотрим треугольники \(MBA\) и \(MCA\): \(\angle M\) – общий, \(\angle BCA = 0,5\cdot\buildrel\smile\over{AB}\). По теореме об угле между касательной и секущей, \(\angle BAM = 0,5\cdot\buildrel\smile\over{AB} = \angle BCA\). Таким образом, треугольники \(MBA\) и \(MCA\) подобны по двум углам.

Из подобия треугольников \(MBA\) и \(MCA\) имеем: \(\dfrac{MB}{MA} = \dfrac{MA}{MC}\), что равносильно \(MB\cdot MC = MA^2\).

 

Следствие

Произведение секущей, проведённой из точки \(O\), на её внешнюю часть не зависит от выбора секущей, проведённой из точки \(O\):

 

Справочник репетитора по математике. Свойства окружности и ее элементов

Теоретические справочные материалы по геометрии для выполнения заданий от репетитора по математике. В помощь ученикам при решении задач.

1) Терема о вписанном угле в окружность.

Теорема: вписанный в окружность угол равен половие градусной меры дуги, на которую он опирается (или половине центрального угла, соответствующего данной дуге), то есть .

2) Следствия из теоремы о вписанном угле в окружность.

2.1) Свойство углов, опирающихся на одну дугу.

Теорема: если вписанные углы опираются на одну дугу, то они равны (если они опираются на дополнителные дуги, их сумма равна

2.2) Свойство угла, опирающегося на диаметр.

Теорема: вписанный угол в окружность опирается на диаметр тогда и только тогда, когда он прямой.

AC-диаметр

3) Cвойство отрезков касательных. Окружность, вписанная в угол.

Теорема 1: если из одной точки, не лежащей на окружности, проведены к ней две касательные, то их отрезки равны, то есть PB=PC.
Теорема 2: Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть PO-биссектриса.

4) Свойство отрезков хорд при внутреннем пересечении секущих.
Теорема 1: произведение отрезков одной хорды равно произведению отрезков другой хорды, то есть

= .

Теорема 2: угол между хордами равен полусумме дуг, которые этими хордами образуются на окружности, то есть

5) Свойство отрезков хорд при внешнем пересечении секущих.

Теорема 1: произведение отрезков одной секущей равно произведению отрезков другой, то есть

= .

Теорема 2: угол между секущими равен полуразности соответствующих им дуг, то есть

Комментарий репетитора по математике: Обратитте внимание на общую закономерность 4-го и 5-го свойства: хорды в произведениях не участвуют, а сами равенства (с частями и продолжениями хорд) при сохранении обозначений являются точной копией друг друга. Также можно подметить общую структуру равенств с дугами. Репетитору по математике стоит обратить на этих особенностях внимание ученика.

6) Свойства квадрата отрезка касательной

Теорема 1: Квадрат отрезка касательной равен произведению отрезков секущей, то есть

Теорема 2:угол между касательной и секущей равен полуразности соответствующих им дуг, то есть

7) Угол между касательной и секущей

Теорема:угол между касательной и секущей, проведенными из одной точки окружности, равен поливине дуги, которую отсекает сукущая (половине центрального угла, соответствующего данной дуге).

.

Колпаков Александр Николаевич, репетитор по математике.

Определение центрального угла

Центральным углом называется угол с вершиной в центре окружности.

Центральный угол рассматривается вместе со своей внутренней областью – одной из двух частей, на которые стороны угла разбивают плоскость. Измеряется в пределах \([0^{\circ}; 360^{\circ}]\).

Определение градусной меры дуги окружности

Градусной мерой дуги окружности называется градусная мера соответствующего ей центрального угла (т. е. центрального угла, который высекает эту дугу на окружности).

$$ \overset{\smile}{AB}=\angle AOB $$

Определение вписанного угла

Угол называется вписанным в окружность, если его вершина лежит на окружности, а стороны пересекают окружность. Говорят, что вписанный угол опирается на дугу, которую он вместе со своей внутренней областью высекает на окружности.

Вписанный угол \(ACB\) опирается на дугу \(AB\).

Теорема о вписанном угле

Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается, и равна половине градусной меры соответствующего этой дуге центрального угла.

$$ \alpha=\frac{1}{2}\beta=\frac{1}{2}\overset{\smile}{AB} $$

Угол, опирающийся на диаметр

Угол, вписанный в окружность, прямой, тогда и только тогда, когда он опирается на диаметр.

\( \angle{ACB}=90^{\circ} \Leftrightarrow \) \(AB\) – диаметр

Признак вписанного четырёхуольника

Если сумма противоположных углов четырёхугольника равна \(180^{\circ}\), то этот четырёхугольник вписанный.

\(\angle{A}+\angle{C}=180^{\circ} \Rightarrow ABCD\) – вписанный

Угол, образованный хордами

Градусная мера каждого из вертикальных углов, образованных двумя пересекающимися хордами, равна полусумме градусных мер дуг, которые эти углы высекают на окружности.

$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}+\overset{\smile}{CD}\right) $$

Угол, образованный касательной и хордой

Градусная мера угла, образованного касательной к окружности и хордой с концом в точке касания, равна половине градусной меры дуги окружности, заключённой внутри этого угла.

$$ \alpha=\frac{1}{2}\overset{\smile}{AB} $$

Угол с вершиной на окружности

Пусть вершина угла принадлежит окружности, а одна из его сторон и продолжение другой стороны пересекают окружность. Тогда градусная мера этого угла равна полусумме градусных мер дуг, которые он вместе с вертикальным ему углом высекают на окружности.

$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}+\overset{\smile}{BC}\right) $$

Угол с вершиной в круге

Градусная мера угла, вершина которого принадлежит кругу, равна полусумме градусных мер дуг, которые этот угол вместе с вертикальным ему высекает на окружности.

\( \alpha=\frac{1}{2} ( \)дуга\(_1\) + дуга\(_2 )\)

Угол, образованный секущими

Градусная мера угла, образованного двумя секущими к окружности, равна полуразности градусных мер дуг, которые он высекает на окружности.

$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}-\overset{\smile}{CD}\right) $$

Угол, образованный касательными

Градусная мера угла, образованного двумя касательными к окружности, равна полуразности градусных мер дуг, на которые точки касания делят окружность.

$$ \alpha=\frac{1}{2}\left(\overset{\smile}{ACB}-\overset{\smile}{ADB}\right) $$

Угол, образованный касательной и секущей

Градусная мера угла, образованного касательной и секущей к окружности, равна полуразности градусных мер дуг, которые этот угол высекает на окружности.

$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}-\overset{\smile}{BC}\right) $$

Признак касания прямой и окружности

Градусная мера угла, образованного касательной и секущей к окружности, равна полуразности градусных мер дуг, которые этот угол высекает на окружности.

$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}-\overset{\smile}{BC}\right) $$

Угол с вершиной вне круга

Если вершина угла лежит вне круга, а каждая сторона пересекает круг или касается его, то градусная мера этого угла равна полуразности градусных мер дуг, которые он высекает на окружности.

\( \alpha=\frac{1}{2} ( \)дуга\(_1\) – дуга\(_2 )\)