Длина дуги окружности. Центральный угол окружности. Дуга большого круга.

В той статье мы узнаем что такое дуга окружности, центральный угол, измерение дуги окружности.

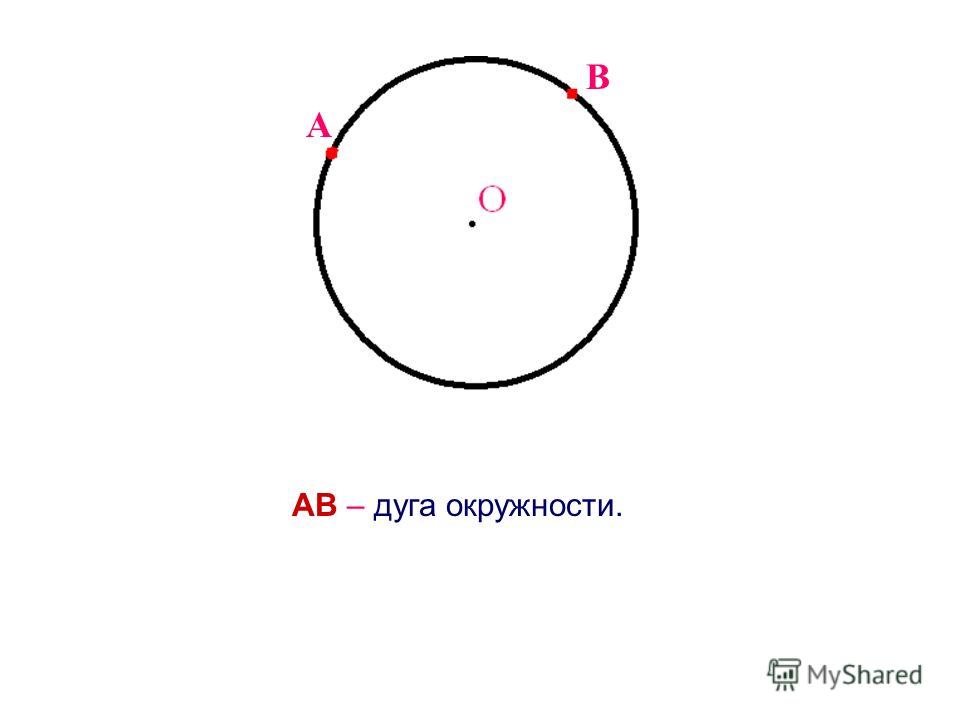
Дуга окружности

Дуга — это любая связанная часть окружности круга. На рисунке ниже часть окружности от \(M\) до \(N\) образует дугу. Она называется \(\smile\) \(MN\).

Дуга может быть малой дугой, полукругом или большой дугой. Полукруг — это дуга, равная половине круга. Малая дуга — это дуга, которая меньше полукруга. Большая дуга — это дуга, которая больше полукруга.

Центральный угол
Центральный угол — это угол, вершина которого находится в центре окружности. Например угол \(∠NAM\):

 

Дуга круга, угол

На приведенной выше диаграмме центральный угол для дуги \(MN\) равен \(45°\).

Сумма центральных углов в любой окружности равна \(360°\). Мера полуокружности равна \(180°\).

Мера малой дуги равна мере центрального угла, который перехватывает дугу.

Можно также сказать, что мера малой дуги равна мере центрального угла, который подтягивается дугой. На диаграмме ниже мера дуги \(MN\) равна \(45°\):

 

Мера главной дуги равна \(360°\).

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Наши преподаватели

Оставить заявку

Репетитор по математике

Челябинский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по английскому языку 4-11 классов.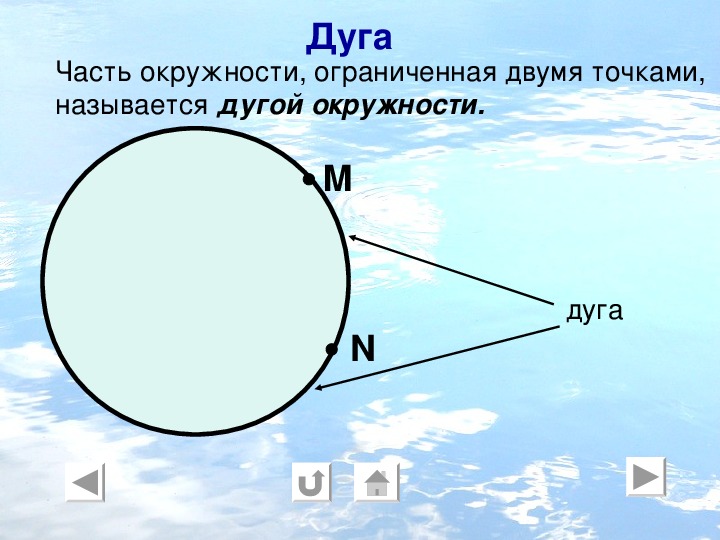

Люблю свой предмет! Радуюсь хорошим результатам своих учеников. К работе подхожу креативно и ответственно. Скучно точно не будет. Индивидуальный подход к каждому ученику гарантирую. Мои уроки проходят с упором на коммуникативную методику. Главная задача- вывести ученика на разговор. Использую в работе все современные пособия и УМК, интересные игры и необычные задания!

Оставить заявку

Репетитор по математике

Южный федеральный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 5-7 классов. Применяю индивидуальный подход в обучении каждого ученика. С моей помощью дети понимают математику и начинают её любить. Смогу дать Вашему ребёнку необходимые знания по предмету. Жду всех на занятиях!

Оставить заявку

Репетитор по математике

Крымский федеральный университет им. Вернадского

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-5 классов. Сложно ? Я докажу тебе обратное ! Математику люблю, за то , что в ней всё подчиняется определенным правилам, которые одинаковы абсолютно для всех. Математика — имеет свои неизменные законы, действующие во все времена , и во всех странах. С легкостью увлеку тебя и пробужу в тебе интерес, к Самой «ЦАРИЦЕ» наук , ее Величество — Математика

Логарифмы (урок)

• — Индивидуальные занятия
• — В любое удобное для вас время
• — Бесплатное вводное занятие

Похожие статьи

Длина сварочной дуги что это такое | Ручная дуговая сварка

Всех приветствую . Если ты начал интересоваться сваркой , то эта статья будет весьма кстати . Сегодня будем говорить о длине дуги . Длина сварочной дуги это промежуток между электродом и деталью в котором происходит электродуговой разряд .

яндекс картинки

яндекс картинки

Длина дуги зависит от диаметра электрода и может быть выбрана в пределах Lдуги = 0.5d — 1.2 d , где d — это диаметр электрода . Для примера возьмем электрод диаметром 3 мм , тогда получается что разбег длины сварочной дуги может составить от 1.5 мм до 3.6 мм . Для получения качественного сварного шва и хорошего проплавления электрод нужно держать как можно ближе к детали . Условно длину дуги разделяют на 3 группы — короткая дуга ( 0.5 — 1 d электрода ) , средняя ( 1-1.2 d электрода ) , длинная дуга ( более 1.5 d электрода ) . Короткой дугой варят швы в нижнем положении ,горизонтальные на вертикальной плоскости и вертикальные , потолочные и корневые швы . Короткую дугу используют в 90 процентах случаев сварки . На короткой дуге получается хорошая защита сварочной ванной и хорошее проплавление детали .

яндекс картинки

яндекс картинки

Среднюю дугу используют для сварки и наплавки в нижнем положении . У дуги средней длины большая площадь нагрева детали и меньше глубина проплавления . А вот длинную дугу использовать вообще не рекомендуется . Здесь можно получить весь букет дефектов сварного шва и этот шов будет весьма сомнительного качества .

яндекс картинки

яндекс картинки

А как вручную определить и выставить эту длину дуги ? Тут только одна рекомендация — немного попрактиковаться и поэкспериментировать . Вы быстро поймете оптимальную длину дуги по качеству получаемого шва и удобству сварки на этой длине дуги , да и еще по звуку сварки — чам длиннее дуга тем громче будет звук . Только на практике , ведь никаких щупов для зазора сварочной дуги пока еще не придумали !

яндекс картинки

яндекс картинки

Надеюсь статья была полезной! Если ты решил самостоятельно осваивать Ручную дуговую сварку, то просто кликай на этот текст, чтобы перейти на главную страницу канала, где можно сразу подписаться и выбрать для себя наиболее интересные статьи!

Центральные и вписанные углы.

Как найти?

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

ㄥAOB = ◡ AB

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

Условия зажигания и устойчивого горения дуги. 1СВ-12.

Спецтехнология

Тема урока: Условия зажигания и устойчивого горения дуги. 1СВ-12. Спецтехнология

Тема урока:  Условия зажигания и устойчивого горения дуги
 
              ОТКРЫТИЕ ДУГОВОЙ СВАРКИ
 
 Замечательный русский изобретатель Н.Г.Славянов был  по образованию инженером, металлургом.
 
  Последняя четверть прошлого века явилась периодом становления электротехники-науки о процессах, связанных с практическим применением электрических явлений. 30-летний руководитель орудийных и механических производств на одном из крупнейших в России пушечных заводов в Перми, Н.Г.Славянов увидел в электротехнике будущее металлургии, обработки металлов. Он глубоко изучил эту область науки.
 
  Через шесть лет после открытия Н.Н.Бенардосом дуговой сварки, в 1888 году Н.Г.Славянов творчески развил эту идею, разработав и применив сварку металлическим электродом. Впервые в мире этот способ был внедрен Славяновым на Пермском  заводе.
 
Он сконструировал и опробовал автоматическое приспособление для регулировки длины дуги. Это был прообраз современных сварочных аппаратов. Изобретение обессмертило его имя и имеет огромное значение и по сей день.
 
  Так Славяновым была написана одна из страниц истории важнейшей области техники – дуговой сварки металлов, находящей самое широкое применение в современной промышленности и строительстве.
 
            ЧТО ТАКОЕ ДУГА                                      
   
 
        Дуга представляет собой электрический разряд в газе между электродами, к которым подведено напряжение источника тока. Ток в дуге обусловлен так называемыми свободными электронами и положительными и отрицательными заряженными частицами вещества – ионами. Процесс образования этих частиц называется ионизацией. В средней части дуги расположен столб дуги, ярко светящейся и имеющей температуру около 6000 градусов по Цельсию. Столб заканчивается на электродах катодным и анодным  пятнами, через которые проходит весь ток дуги. Плотность тока на пятнах весьма велика, благодаря чему в этих зонах происходит интенсивное нагревание до температуры испарения материала электродов. Столб дуги окружает пламя – раскалённые пары и газы, температура которых резко падает по мере удаления от столба. Дугу перемещают при сварке вручную или механически вдоль кромок соединяемых деталей, благодаря чему достигается  непрерывное плавление их и образование соединения – сварного шва. Глубиной проплавления называется наибольшая глубина расплавления основного металла в сечении шва.
 
 
 
        РАСПРОСТРАНЕНИЕ ДУГОВОЙ СВАРКИ
 
        Особенно широкое распространение получила дуговая сварка Н.Г.Славянова. Сущность этого способа заключается в том, что электрическая дуга возбуждается между свариваемой деталью и металлическим электродом, который плавится в процессе горения дуги и заполняет тем самым сварной шов. Одновременно плавятся корки свариваемых деталей. Такой процесс называется сваркой металлическим электродом.
 
 
 
    В ЗАВИСИМОСТИ ОТ СПОСОБА ДУГОВОЙ СВАРКИ
 
 
        В зависимости от способа дуговой сварки, т.е. от материала применяемого электрода, свойства электрической дуги меняются. Так, при горении дуги между свариваемым металлическим изделием и угольным электродом дуги имеет большую длину и несколько иную форму чем дуга, горящая между изделием и металлическим электродом. В последнем случае явления, происходящие в дуге, значительно сложнее, так как в дуговом промежутке по мимо паров, образуемых при сгорании электрода, присутствуют капли расплавленного и пары сгорающего в дуге электродного покрытия. Если дуговая сварка по способу Бенардоса производится голым угольным электродом, то при сварке по способу Славянова на плавящийся металлический электрод обычно наносится покрытие, в зависимости от состава и толщины наносимого слоя может быть ионизирующим либо так называемым качественным, т.е. обеспечивающим получение повышенного качества наплавленного металла.
 
       Ионизирующие  покрытия  наносятся  на  электрод  слоем,  не  прерывающим  по толщине  0,3-0,5  мм;  в  состав  этих  покрытий  входят  обычно  вещества,  ионизирующие дуговой  промежуток,  т.е.  способствующие  устойчивому  горению  дуги  даже при  питании  её  от  источника  переменного  тока.  Ионизирующее  покрытие никакой защиты металла от воздуха не осуществляется.
 
       Качественные покрытия наносятся на электрод слоем, достигающим по толщине 1,5 –3 мм; в состав этих покрытий входит шлакообразующие и газообразующие вещества, защищающие жидкую ванну и капли электродного металла от окружающего воздуха; вещества, способствующие ионизации дуги, а также некоторые легирующие элементы, улучшающие механические свойства наплавленного металла. За счет правильного подбора электродных покрытий сварной шов во многих случаях получает механические свойства более высокие, чем основной свариваемый металл.
 
        Сварка угольным электродом стали, а также чугуна и цветных металлов производится с применением флюса, наносимого на присадочные стержни и на  кромки свариваемых деталей.
 
Различают сварку током примой и обратной полярности. Прямая полярность – это когда положительный вывод источника сварочного тока присоединён к свариваемым изделиям, а отрицательный – к электрод держателю. При этом в дуговом разрядном промежутке изделие являются анодом, а электрод – катодом.
 
        В дуге действует механические силы, направленные вдоль столба дуги (дутье). Под действием этих сил в жидком металле сварочной ванны образуется лунка, так называемый кратер. В конце швов при затвердевании металла в результате его усадки также образуется углубление, которое называется конечным кратером. Конечный кратер при необходимости либо заваривают, повторно расплавляя металл в этом месте, либо шов выходят на  планку, которая удаляется после сварки. При сварке шин с этой же цели швы выводятся в лунке угольных брусков, формующих стыки шин с торцов.
 
                
         
Тестирование
                     
                     Вопросы на тестирование
 

Электрическая дуга — это:
Сварочная дуга
Строение сварочной дуги
Средний
Длительный устойчивый электрический заряд в газовой среде между электродами.
Дуга, образующая лазерным излучением.
Это дуга, образующая плазменной струей
Это электрическая цепь с источником питания.
Электрическая искра в месте разрыва цепи.
Сварка — это процесс получения:
Сварочная дуга
Строение сварочной дуги
Минимальная
Неразъемных соединений
Разъемных соединений
Клепаных соединении
Болтовых соединений
Клееных соединений
Задание №54	Страна где была изобретена электросварка
Раздел
Тема
Сложность
Верный	Россия
Неверный	США
Неверный	Швеция
Неверный	Франция
Неверный	Италия
Задание №55	Дефект сварного шва при не сплавлении основного металла с металлом шва
Раздел
Тема
Сложность
Верный	Непровар
Неверный	Подрез
Неверный	Прожег
Неверный	Трещина
Неверный	Газовые поры
Задание №56	Подрезы относятся к дефектам
Раздел
Тема
Сложность
Верный	К наружным
Неверный	К микроструктурным
Неверный	К наружным и внутренним
Неверный	Нет таких дефектов
Неверный	К внутренним
Задание №57	Если в процессе сварки отсутствует провар сварщик должен
Раздел
Тема
Сложность
Верный	Прекратить сварку ,устранить дефект и изменить режим сварки
Неверный	Поменять переменный ток на постоянный
Неверный	Поменять марку электрода
Неверный	Поменять полярность сварки
Неверный	Произвести доварку шва
Задание №58	Электрошлаковую сварку применяют для сварки стальных деталей толщиной
Раздел
Тема
Сложность
Верный	От 25мм –до 1000 мм
Неверный	От 10мм –до 50мм
Неверный	От 2 мм –до 10мм
Неверный	От 7 мм –до 30мм
Неверный	От 5 мм –до 20мм
Задание №59	Сварной шов это
Раздел
Тема
Сложность
Верный	Элемент сварного соединения ,образовавшийся после кристаллизации расплавленного металла
Неверный	Элемент шва после заклепки
Неверный	Элемент прихватки
Неверный	Элемент шва в месте резьбового соединения
Неверный	Элемент шва после болтового соединения

Сварочная дуга.

Описание и характеристики

Для того чтобы успешно провести процесс сварки, необходима сварочная дуга. Это электрический разряд, который характеризуется очень высокой мощностью и является достаточно длительным. Возникает он между такими элементами, как электроды, которые находятся в определенной газовой среде. Для возникновения дуги необходимо подать напряжение на электроды.

Общее описание дуги

Основные отличительные свойства сварочной дуги — это очень высокая температура, а также плотность тока. Благодаря этим двум качествам в совокупности дуга способна без проблем плавить металлы, температура плавления которых составляет 3000 градусов по Цельсию. Можно сказать, что данная дуга является проводником, который состоит из летучих веществ, а основное предназначение — это преобразование электрической энергии в тепловую. Сам же электрический заряд — это момент прохождения электрического тока через газовую среду.

Разновидности разряда

Сварочная дуга — это разряд, а так как существует несколько его видов, то выделяют и несколько видов самой дуги:

1. Первая разновидность называется тлеющим разрядом. Возникает такой вид только в среде с низким давлением, и применяется только в таких вещах, как плазменные экраны или же люминесцентные лампы.
2. Второй тип — это искровой разряд. Возникновение такого вида происходит в тот момент, когда давление будет примерно равно атмосферному. Отличается тем, что имеет довольно прерывистую форму. Яркий пример такого разряда — молния.
3. Сварочная дуга — это дуговой разряд. Именно этот тип чаще всего используется во время сварки. Возникает он при наличии атмосферного давления, а его форма непрерывна.
4. Последний тип называется коронным. Чаще всего возникает в том случае, если поверхность электрода отличается шероховатостью и неоднородностью.

Природа дуги

Стоит сказать, что электрическая сварочная дуга не так уж и сложна, как кажется на первый взгляд, понять ее природу достаточно просто. Здесь применяется электрический ток, который протекает через такой элемент, как катод. После этого он попадает в среду с ионизированным газом. В этот момент и возникает разряд, который характеризуется ярким светом и очень высокой температурой. Вообще, сварочная дуга может иметь температуру в пределах от 7000 до 10 000 градусов по Цельсию. После прохождения этого этапа ток будет переходить на материал, который подвергается сварке. Можно сказать, что источник сварочной дуги — электрический ток, который подвергся изменениям.

Из-за настолько высоких температур дуга будет излучать инфракрасные и ультрафиолетовые лучи, которые вредны для здоровья человека. Это опасно для глаз человека, а также может оставить световой ожог. По вышеуказанным причинам все сварщики должны иметь хорошие индивидуальные средства защиты.

Строение дуги

Строение (структура) сварочной дуги включает в себя три основных компонента, или участка — анодный и катодный участок, а также столб дуги. Стоит отметить, что во время горения сварочной дуги на участках анода и катода будут образовываться активные пятна или области, которые характеризуются максимальным значением температуры. Через эти две области будет проходить весь электрический ток, который вырабатывает источник питания. В это же время наибольшее падение напряжения сварочной дуги будет также фиксироваться на этих двух участках. Столб дуги же находится между этими двумя зонами, а такой параметр, как падение напряжения, в данном случае будет минимальным.

Из всего вышесказанного можно сделать вывод, что, во-первых, источник питания сварочной дуги может выдавать довольно высокое напряжение и ток большой силы. Во-вторых, длина дуги будет состоять из совокупности тех областей, которые были перечислены выше. Чаще всего длина такой дуги равна нескольким миллиметрам, при условии, что анодная и катодная области соответственно равны 10-4 и 10-5 см. Наиболее благоприятной длиной считается дуга 4-6 мм. Именно при таких показателях удастся достичь стабильного горения и высокой температуры.

Виды дуги

Отличие сварочной дуги заключается в схеме подвода, а также в среде, в которой она может возникать. В настоящее время существует два наиболее распространенных типа дуги:

• Дуга прямого действия. В таком случае сварочный аппарат должен располагаться параллельно по отношению к объекту, который подвергается сварке. Электрическая дуга будет возникать, когда угол между металлической заготовкой и электродом составит 90 градусов.
• Вторая основная разновидность — сварочная дуга косвенного типа действия. Она возникает только в том случае, если используется два электрода, и расположены они под углом в 40-60 градусов по отношению к поверхности металлической детали. Дуга будет возникать между этими двумя элементами и сварит металл между собой.

Классификация

Стоит отметить, что есть классификация дуги в зависимости от атмосферы, в которой она будет возникать. На сегодняшний день известно о трех типах:

• Первый тип — это открытая дуга. При сварке такого типа дуга будет гореть на открытом воздухе, а вокруг нее будет образовываться небольшой газовый слой, в который войдут пары металла, электродов и их покрытия.
• Закрытый тип. Горение такой сварочной дуги характеризуется тем, что осуществляется под слоем флюса.
• Последняя разновидность — это дуга с подачей газа. В таком случае в нее подается такое вещество, как гелий, аргон или углекислый газ. Можно использовать и некоторые другие типы газов.

Основное отличие последнего типа заключается в том, что подаваемые газы будут препятствовать такому явлению, как окисление металла во время сварки.

Небольшое отличие наблюдается и в плане времени действия такой дуги. По своей характеристике сварочная дуга может быть стационарной или же импульсной. Стационарная применяется при непрерывном сваривании металлов, то есть она непрерывна. Импульсный тип дуги — это однократное воздействие на металл, точеное прикосновение.

Рабочие элементы, то есть электроды, могут быть угольными или вольфрамовыми. Эти электроды также называются неплавящимися. Можно использовать и элементы из металла, однако они будут плавиться так же, как и заготовка. Наиболее распространенным типом электрода является сталь, если говорить о плавящихся типах. Однако применение неплавящихся видов становится все более популярным на сегодняшний день.

Момент возникновения дуги

Сварочная дуга возникает в тот момент, когда происходит быстрое замыкание. Такое случается, когда электрод соприкасается с металлической заготовкой. Из-за того, что температура просто огромна, металл начинается плавиться, а между электродом и заготовкой возникает тоненькая полоса из расплавленного металла. Когда электрод и металл расходятся, то последний практически моментально испаряется, так как плотность тока очень велика. Далее происходит ионизация газа, из-за чего и появляется сварочная дуга.

Условия горения дуги

В стандартных условиях, то есть при средней температуре 25 градусов и давлении в 1 атмосферу, газ не способен проводить электрический ток. Основное требование к возникновению дуги — это ионизация газовой среды между электродами. Другими словами, газ должен иметь в своем составе некоторые заряженные частицы, электроны или ионы.

Второе важное условие, которое необходимо соблюдать, — постоянное поддержание температуры на катоде. Значение требуемой температуры будет зависеть от таких характеристик, как природа катода, а также его диаметр и размер. Важную роль сыграет и температура окружающей среды. Сварочная дуга должна быть стабильной и при этом иметь огромную силу тока, который и даст высокий температурный показатель (7 тысяч градусов по Цельсию и более). Если все условия соблюдены, то полученной дугой можно обрабатывать любой материал. Чтобы обеспечить наличие постоянной и высокой температуры, нужно чтобы источник питания функционировал максимально стабильно. Именно по этой причине источник питания является важнейшей частью при выборе сварочного аппарата.

Особенности дуги

Есть несколько моментов, которые отличают сварочную дугу от других электрических разрядов.

Первое — это огромная плотность тока, которая может достигать нескольких тысяч ампер на один квадратный сантиметр. Это дает огромную температуру во время работы. Распределение электрического поля между электродами в их пространстве достаточно неравномерное. Около этих элементов наблюдается сильное падение напряжение, а к центру же, наоборот, оно сильно уменьшается. Нельзя не сказать о зависимости температуры от длины столба. Чем больше длина, тем хуже нагрев, и наоборот. Используя сварочные дуги, можно получить самую разную вольт-амперную характеристику (ВАХ).

Сварочный инвертор. Дуга и ее особенности

Сразу стоит начать с основного отличия инверторного источника питания от обычного, трансформаторного. Потребление электрической энергии уменьшено почти в два раза. Характеристика тока, который возникает при использовании инвертора, позволяет обеспечить более быстрое зажигание дуги, а также обеспечивает стабильное горение на протяжении всего процесса работы.

Сам по себе сварочный инвертор — это достаточно сложный аппарат, который производит операции по изменению тока для обеспечения максимально стабильной работы дуги. К примеру, прибор подключается к сети и получает на вход переменный ток, который он способен преобразовать в постоянный. Далее постоянный ток поступает в блок блок инвертора, где он снова преобразовывается в переменный, но уже с гораздо большей частотой, чем был в сети. Этот ток передается трансформатору, где значительно снижается его напряжение, из-за чего увеличивается его сила. После этого выпрямленный и настроенный переменный ток передается выпрямителю, где он преобразовывается в постоянный и подается для работы.

Сварочная дуга: все, что вы хотели знать

Уже более полувека сварка является одним из важнейших ремесел для человека. Благодаря сварочному аппарату строятся космические корабли, функционируют заводы, и для многих умельцев сварка превратилась в хобби. Но даже самый технологичный сварочный аппарат не принесет желаемого результата без стабильной сварочной электрической дуги и ее качественных характеристик.

Электрическая сварочная дуга позволяет надежно сварить даже самые сложные конструкции из металла. Чтобы получить качественные сварные швы нужно учесть все ее характеристики, знать особенности и строение дуги. Дополнительно важно учитывать температуру и напряжение дуги при ручной дуговой сварке. Из этой статьи вы узнаете, что такое сварочная дуга и сущность протекающих в ней процессов, научитесь применять полученные знания на практике.

Содержание статьи

• Сварочная дуга: определение
• Суть и строение дуги
• Виды сварочной дуги
• При каких условиях горит дуга
• Особенности дуги
• Вместо заключения

Сварочная дуга: определение

Итак, что такое сварочная дуга и каковы ее характеристики? Электроды, находящиеся под напряжением в смеси газов и паров, формируют мощный разряд. Что называется электрическим разрядом? Разряд — это результат прохождения электрического тока через газ. Ну а результат всего процесса в целом называют сварочной дугой. Сварочная дуга и ее свойства отличаются большой температурой и плотностью тока, поэтому дуга способна расплавить практически любой металл. Говоря более простыми словами, сварочная дуга является отличным проводником, преобразующим получаемую электрическую энергию в тепловую. За счет этой тепловой энергии и плавится металл.

Суть и строение дуги

Суть сварочной дуги крайне проста. Давайте разделим процесс на несколько пунктов:

• Сначала электрический ток проходит через катодную и анодную область и проникает в газовую среду. Формируется электрический разряд с сильным свечением.
• Образуется дуга. Температура сварочной дуги может доходить до 10 тысяч градусов по Цельсию, а этого достаточно, чтобы расплавить практически любой материал.
• Затем ток с дуги переходит на свариваемый металл. Вот и все ее характеристики.

Свечение и температура разряда настолько сильны, что могут нанести ожоги и лишить сварщика зрения. Поэтому мастера используют сварочные маски, защитные перчатки и костюм. Ни в коем случае не занимайтесь сваркой без надлежащей защиты.

Строение сварочной дуги представлено на картинке ниже.

В области катода и анода во время горения дуги образуются пятна, где температура достигает своего предела. Именно через анодные и катодные области проходит электрический ток, при этом в этих областях напряжение значительно падает, а на столбе напряжения сварочной дуги сохраняется, поскольку столб располагается между анодом и катодом. Многие новички спрашивают, как измерить длину дуги. Достаточно посмотреть на катодную и анодную область, а также на сварочный столб. Их совокупность и называется длинной сварочной дуги. Средняя длина составляет 5 миллиметров. В этом случае температура получаемой тепловой энергии оптимальна и позволяет выполнить большинство сварочных работ. Теперь, когда мы узнали, что сварочная дуга представляет собой, обратимся к разновидностям.

Виды сварочной дуги

Сварочная дуга и ее характеристики могут отличаться по прямому и косвенному действию сварочного тока, а также по атмосфере, в которой они формируются. Давайте разберем эту тему подробнее.

Прямое действие сварочной дуги характеризуется особым направлением тока. Электрод располагается почти параллельно свариваемой поверхности и при этом дуга формируется под углом в 90 градусов. Электрическая сварочная дуга и ее характеристики могут быть и косвенного действия. Она может формироваться лишь с использованием двух электродов, расположенным под углом над поверхностью свариваемой детали. Здесь так же возникает сварочная дуга и металл плавится. Как мы писали выше, сварочные дуги также делятся по атмосфере, в которой формируются. Вот их краткая классификация:

• Открытая среда. В открытой среде (атмосфере) дуга формируется за счет кислорода из воздуха. Вокруг нее образуется газ, содержащий пары свариваемого металла, выбранного электрода и его покрытия. Это самая распространенная среда при дуговой сварке.
• Закрытая среда. В закрытой среде дуга горит под толстым слоем защитного флюса при этом так же формируется газ, но содержащий не только пары металла и электрода, а еще и пары флюса.
• Газовая среда. Дугу поджигают и подают один из видов сжатого газа (это может быть гелий или водород). Дополнительная подача сжатого газа также защищает свариваемые детали от окисления, газы формируют нейтральную среду. Здесь, как и в остальных случаях, формируется газ, который содержит пары металла, электрода и сжатый газ, который сварщик дополнительно подает во время горения дуги.

Еще сварочные дуги могут быть стационарными и импульсными. Стационарные используют для долгой кропотливой работы без необходимости частого перемещения дуги. А импульсную используют для быстрой однократной работы.

Также сварочная дуга и ее характеристики могут косвенно классифицироваться по виду используемого в работе электрода (например, угольного или вольфрамового, плавящегося и неплавящегося). Опытные сварщики чаще всего используют неплавящийся электрод, чтобы лучше контролировать качество получаемого сварного соединения. Как видите, процесс сварки простой сварочной дугой может иметь множество особенностей, и их нужно учитывать в своей работе.

При каких условиях горит дуга

В обычном цеху или в вашем гараже средняя температура составляет 20 градусов по Цельсию, а давление не превышает одной атмосферы. В таких условиях газ практически не способен проводить электрический ток и тем самым формировать дугу. Для решения этой проблемы нужно добавить ионы в образующиеся газы. Вот что называют ионизацией профессиональные мастера.

Также в катодной области нужно постоянно поддерживать постоянную температуру. Это необходимо, чтобы дуга возникла и поддерживала горение. Но поскольку именно в области катода и анода температура может снижаться быстрее, у многих новичков возникает масса проблем. Кроме того, температура области катода может сильно варьироваться в зависимости от температуры в помещении, где проходит сварочный процесс. Проблем можно избежать, если следить за исправностью источника питания и стабильностью подачи электричества (особенно важный момент для домашних сварщиков с нестабильным напряжением в бытовой электросети). Все это оказывает большое влияние на свойства сварочной дуги и сущность протекающих в ней процессов.

Особенности дуги

Сварочная дуга и ее характеристики обладают рядом особенностей, которые нужно учитывать в своей работе:

• Как мы неоднократно говорили, у дуги очень высокая температура. Она достигается за счет большой плотности электрического тока (плотность может достигать тысячи ампер на квадратный сантиметр). По этой причине важно правильно настроить аппарат и быть осторожным при сварке тонких металлов.
• Электрическое поле неравномерно распределяется между электродами, если их используется две штуки. При этом в сварочном столбе напряжение практически не меняется, а вот в катодной области это напряжение заметно снижается, что может привести к ухудшению качества шва.
• В сварочном столбе, в свою очередь, наблюдается самый высокий показатель температуры, чего нельзя сказать о других частях дуги. Учтите, что если вам необходимо увеличить длину дуги, то вы скорее всего потеряете часть этой температуры. Этот показатель особенно важен при сварке металлов с высокой температурой плавления.

Еще с помощью выбора плотности тока можно регулировать падение напряжения сварочной дуги. Чем выше плотность тока, тем выше вероятность, что напряжение сварочной дуги упадет. Но бывают случаи, когда от нарастающей силы тока напряжение сварочной дуги увеличивается. Чтобы контролировать этот процесс понадобится некоторый опыт. Не бойтесь экспериментировать, если вам позволяет работа. Это были основные свойства сварочной дуги, на которые следует обратить внимание.

Вместо заключения

Теперь вы знаете все о сварочной дуге и ее свойствах, а также знаете  ее характеристики. Опытные сварщики могут в комментариях поделиться своим пониманием, что из себя представляет сварочная дуга и сущность протекающих в ней процессов. Это будет особенно полезно для начинающих сварщиков.

Кратко резюмируя, сварочная дуга состоит из сварочного столба, анодных и катодных областей. Именно в этих областях проходит ток. В результате формируется электрический разряд. Образуется дуга и преобразовывает полученный ток в тепло, температура может достигать 10 тысяч градусов по Цельсию!
Саму дугу можно зажечь с помощью двух методов: чирканья и постукивания. Новички предпочитают метод постукивания, но мы рекомендуем освоить и метод чирканья, поскольку это улучшит ваши профессиональные навыки и предотвратит от залипания электродов. Желаем удачи!

Углы в окружности

здравствуйте наши любимые ученики в честь праздника пятница 13 который уже минул у нас сегодня для вас 9 кругов ада [музыка] вот они и мы сейчас с вами их и пройдем а я за мелом кстати чтобы вся ваша учёба не превращалась 9 кругов ада я рекомендую вам зарегистрироваться у нас на сайте каждый найдет репетитора по своему предмету регистрируйтесь и для каждого нового ученика бесплатный урок подарок на повестке дня углы в окружности если вы продвинутый пользователь ты вы уже знаете что это такое а для тех кто только сегодня с этим познакомиться немножко истории это такие углы которые будут рисоваться внутри окружности и различают их два вида это центральные углы те которые выходят из центра и вписанные углы у которых вершина лежит на окружности про эти углы есть немножко информация о том что к примеру вписанный угол он опирается на какую-то дугу вот посмотрите куда идут его ноги это и есть дуга на которой он опирается и центральный угол он тоже всегда опирается на какую-то дугу есть кое-какая взаимосвязь вот этот центральный угол он как раз делает ту самую дугу в такую же градусную меру то есть если здесь написано 80 градусов то дуга обед также будет восемьдесят градусов если угол как здесь вписанный а cb то он как раз таки в два раза меньше чем то дуга на которую опирается получается что здесь угол будет равен 40 градусов вот этим правилам в основном и пользуются когда решают подобные задачи сами того не подозревая мы решили уже первую задачу мы нашли чему равен угол от cb связь между вписанным и центральным углом если они опираются на одну и ту же дугу то вписанный угол в два раза меньше чем центральный и наоборот если вы будете знать вписаны вы всегда сможете найти центральный за счет той дуги на которую они опираются картинка номер два что мы здесь видим окружность и два каких-то угла надо их распознать a b c это вписанный угол вот его вершина и а отце это центральный потому что выходит из центра что от нас хотят угол а у c центральный значит используя те правила которые мы обсуждали в первая задача можно сказать что угол а отце в два раза больше чем угол a b c даже не подключая вот эту дугу только запомнить вот эти два соотношения как какое-то готовое правило 65 умножить на 2 значит угол равен 130 градусов задача решена смотрим дальше что здесь нарисован какой-то треугольник а cb от нас хотят угол а cb опять же для чего нарисована окружность наверное речь пойдет об углах если рассмотреть угол от cb он является не только частью треугольника но и вписанным углом который опирается на а б у нас это диаметр это показано чертеже потому что . а это центр что получается он опирается на дугу от а до б а диаметр deered окружность на 2 равные части значит обе дуги будут по 180 градусов потому что вся окружность 360 если этот угол 180 по нашим правилам вот этот угол one в два раза меньше чем то дуга к на которого набирается если здесь 180 значит данных угол будет 90 и это использует задачах как уже готовый результат если вы встречаетесь треугольником который опирается на диаметр всегда пользуйтесь тем что он будет прямоугольник как бы вы его тут не расположили как люблю говорить даже если мы нарисуем вот какой-нибудь супер скошенный треугольник все равно вот этот угол будет давать 90 градусов потому что он опирается на диаметр этим пользуйтесь уже как готовым результатом начинаем усложняться если до этого мы использовали просто какие-то основные правила сейчас нам дают какой-то чертеж в котором какая-то бабочка внутри окружности разберитесь ситуацией и посмотрите вообще что от вас хотят к примеру у нас просят найти угол b и d вот он бмд что рекомендую делать проследить и куда идут ноги этого угла от этого будет зависеть от какой дуги зависит этот угол он опирается на вот эту дугу бды у нас внимание есть еще один угол который равен 40 градусам это угол b c d и он стоит своими ногами тоже на этой дуге если два вписанных угла опираются на одну и ту же дугу то они будут между собой равны как это можно объяснить если здесь 40 градусов значит дуга будет два раза больше по правилам вот этого вписанного угла если здесь 80 то вот этот наш угол он стоит на ней же поэтому он тоже быть в два раза меньше чем эта дуга получается 40 но чтобы вот этим не запариваться каждый раз вы можете запомнить как готовое правила о том что если вписанные углы опираются на одну и ту же дугу то они равны между собой кстати нарисовать этих углов вы можете сколько угодно посмотрите я могу вот так даже в сторону скосить угол и его она и ту же дугу оперетте он тоже будет равен 40 градусам пользуйтесь вот это правило очень популярна таких задачах ну и теперь на очереди задача номер 5 поехали скоро продолжаем разговор перед нами чертеж здесь уже нет никакого угла внутри окружности есть bc это у нас касательная вот точка касания и какая-то хорда б. а. говорят что дуга б д а вот она б д а вот она равна 240 градусов и надо найти угол a b c опять же повторюсь если вы продвинутый пользователь возможно вы уже видели формулу которая говорит как найти этот угол он зависит от вот этой вот дуги б.а. но это правило которое уже вывели и вы им просто пользуетесь сейчас немножко объясним как к этому прийти если посмотреть на дугу которая на 240 она относится к б д а то мы можем перейти к дуге б.а. каким образом если эта вся окружность 360 градусов а здесь 240 на эту дугу у нас остается 120 градусов что с этими градусами делать естественно просто летающие полки они не несут никакой информации мы можем особенно учитывая что у нас есть точка касания нарисовать центр и выстроить треугольник б о а что это за треугольник он будет равнобедренным потому что это радиус они равны и этот угол б а а он является центральным раз он центральный значит он равен то иду гены которого он опирается здесь 120 градусов что еще интересного если это радиус проведенный в точку касания то весь угол целиком будет 90 градусов это кстати в предыдущем видео можно посмотреть если вы подзабыли далее если треугольник равнобедренный значит у него углы при основании равны получается что на угол b вот этот маленький и на угол а будет приходиться 60 градусов 180 минус 120 60 и делим пополам здесь по 30 градусов эти уголки по 30 градусов и теперь использую информацию о том что здесь угол 90 90 минус 30 получаем 60 этот угол о котором спрашивалось задачи a b c он равен 60 градусов и теперь внимание повторюсь как я некоторым отвечала можно посмотреть как это уже кто-то вывел и воспользоваться этим дальше не выводя каждый раз и значит запоминаем если вы встречаетесь такой ситуации когда идет касательная корда или еще называют секущие то вот эта дуга которая образовалась и вот этот угол они взаимосвязаны и угол который образован между касательной и секущей равен половине дуги которые он отсекает если здесь 120 вот мы получили 60 градусов зачем выводить каждый раз то что уже вывели как правило просто пользуйтесь а мы едем дальше 6 задача простите на кортаны я уже садится не буду буду рассказывать вот так что нам дано акция дуга равна 40 градусам буду сразу рисовать здесь 40 градусов в. д. дуга вот она 100 градусов обращаю внимание вот эту . к это просто какая-то точка внутри окружности это никакой не центр то есть этим пользоваться нельзя что от нас хотят угол b к d где он здесь находится угол b к d вот он как решать эту задачу опять же может быть уже кто-то до нас это решил и вывел какой-то закон соотношение между вот этими вот дугами но мы не будем идти по легкому пути мы попробуем найти этот угол как когда вы видите какие то как я говорю летающие полки внутри окружности это не несёт никакой информации надо достроить до фигуры тем более раз здесь у нас к . это не центр что можно попробовать сделать ну а почему бы нам не провести вот так вот а б корду что нарисовалась у нас есть угол b и d который опирается на дугу в 100 градусов что это за угол такой ноги вот они пошли сюда и это угол который у которого вершина лежит на окружности значит он вписанный и он равен тремя обозначим половине дуги на которую он опирается получается что здесь 50 градусов и теперь подумаем как же нам попытаться прийти вот к этому углу можно работать с какими-то треугольниками ведь правда если бы мы вот в этом треугольнички которые у нас тут образовался знали угол вот он синеньким обозначу то мы смогли бы посчитать вот этот желтый угол потому что они были бы смежные значит надо поработать именно с этим синеньким треугольником и найти в нем те самые углы если этот угол 50 вот мы с помощью этой дуги распознали теперь давайте обратимся в другую сторону угол a b c он же своими ногами идет как раз на дугу в 40 градусов значит раз он вписан и будет два раза меньше чем эта дуга вот и прояснилось что вот этот угол у нас будет равен 20 градусов с треугольником а к б остается самая малость 5020 значит третий угол будет равен 110 градусов 50 плюс 2070 а сумма 180 значит он вот этот уголок я сюда его нарисую 110 градусов и теперь если этот 110 этот смежный с ним и в сумма дает 180 значит он будет равен 70 градусов можно было бы воспользоваться тем что это внешний угол треугольника а к б а внешний угол равен сумме двух не смежных с ним углов то есть 50 плюс 2070 если вы это правило помните можете конечно пользоваться получился что у нас ответ 70 градусов тот угол о котором у нас спрашивали в задаче и кстати оказавшись такой ситуации тот кто запомнит может пользоваться уже готовым правилам то что сумму вот этих дуг можно поделить на 2 и мы как раз получим тот самый угол который получается при писить пересечении двух прямых вот и все задачка номер семь что мы видим есть какая-то . вне окружности идут две секущие здесь образуются дуги cd причем на дают информацию что эта дуга равна 70 вот она и 2 дуга об с этой стороны которая равна 30 градусов от нас хотят угол м что делать до опять же можно воспользоваться уже готовой формулой но мы не ищем легких путей мы попытаемся ее вывести а потом если у вас получится и запомнить пользуйтесь что делать опять же какие-то висящие полки в окружности это нас не устраивает достроен до фигуры чтобы образовались какие-то углы что сделаем но предлагаю провести вот такой отрезок а.д. что образовалась если обратите внимание есть угол c и d который будет вписанным и он равен половине этой дуге на которой он опирается значит здесь 35 градусов и пользуясь кстати тем что у нас здесь развернутый угол вот эти углы смежные значит вот этот уголок будет равен 100 45 градусов далее если обратите внимание а д б это опять же у нас угол который является вписанным и он опирается на дугу в 30 градусов значит вот этот угол будет в 2 раза меньше то есть 15 градусов вы наверно уже догадались что всеми своими силами пытаемся прийти в этот треугольник дым и оттуда мы легко смогли бы найти угол м что мы уже знаем 15 145 все проблем нет можно найти третий угол сколько он будет эта сумма 160 значит этот уголок равен 20 градусам вот и все двадцать градусов а как он готовом провели шла речь в начале дело в том что в такой ситуации вы можете взять вот эту дугу которая 70 градусов было у нас взять вот эту дугу 30 градусов и это минус это и поделить на 2 это и есть правило по которому сразу можно посчитать угол в такой ситуации 70 минут 30 40 40 день пополам 20 тот самый угол м вот так едем дальше задача номер 8 что здесь окружность здесь внутри какая-то бабочка и от нас хотят угол cmd ну ребят что могу сказать задач какая-то элементарная поэтому вам она идет как домашнее задание пожалуйста все свои ответы пишите в комментариях обязательно прослежу и отвечу если будут вопросы да да вижу ваш вопрос и здесь тоже есть домашнее задание а мы едем дальше вот мы и пришли к 9 задачи тот самый девятый круг ада ну здесь не так все страшно как могло показаться самом начале что мы видим и что от нас хотят окружность здесь какая-то фигура не обращайте внимание давайте посмотрим на углы здесь просят угол a b c вот он отдают угол а отце . а это центр окружности ну как рассуждать что такое угол a b c который от нас хотят и куда идут его ноги они идут на дугу акция и если бы вы знали дугу ация то вы бы легко нашли угол a b c он был был равен половине дуги на которую он опирается значит наша цель найти эту дугу и все просто потому что есть угол а отце который является центральным он равен 100 градусов значит то дуга на которую он стоит а это дуга a b c тоже равна 100 градусам ну и теперь осталось очень просто это 360 -100 260 это вот та самая дуга которая нас интересовало и угол a b c он в два раза меньше чем то округа на которой он стоит значит 130 градусов инго и все круги ада мы прошли с вами успешно ура ну а всем тем кто прошел со мной вместе эти 9 кругов ада привет ставьте лайки пишите коментарии всем отвечаю всех люблю а вы распространяйте это видео чтобы и вашим друзьям эта тема показалась раем пока пока у а я оставлю тут для вас еще парочку полезных видео вы можете посмотреть их по ссылкам я думаю не буду тоже вам полезно счастлива

Дуга окружности — объяснение и примеры

После радиуса и диаметра еще одна важная часть окружности — это дуга . В этой статье мы обсудим , что такое дуга, найдем длину дуги и измерим длину дуги в радианах. Мы также изучим малую дугу и большую дугу.

Что такое дуга круга?

Дуга окружности — это любая часть окружности. Напомним, окружность круга — это периметр или расстояние вокруг круга.Следовательно, мы можем сказать, что окружность круга — это полная дуга самого круга.

Как найти длину дуги?

Th e Формула для расчета дуги утверждает, что:

Длина дуги = 2πr (θ / 360)

Где r = радиус окружности,

π = pi = 3,14

θ = угол ( в градусах ), ограниченный дугой в центре круга.

360 = угол одного полного поворота.

На приведенном выше рисунке длина дуги (нарисованная красным) — это расстояние от точки A, до точки B.

Давайте разберемся с несколькими примерами задач о длине дуги:

Пример 1

Учитывая эту дугу, AB образует угол 40 градусов к центру окружности с радиусом 7 см. Рассчитайте длину дуги AB.

Решение

При r = 7 см

θ = 40 градусов.

Путем подстановки

Длина дуги = 2πr (θ / 360)

Длина = 2 x 3,14 x 7 x 40/360

= 4,884 см.

Пример 2

Найдите длину дуги окружности, которая образует угол в 120 градусов с центром окружности на 24 см.

Решение

Длина дуги = 2πr (θ / 360)

= 2 x 3,14 x 24 x 120/360

= 50,24 см.

Пример 3

Длина дуги 35 м.Если радиус круга равен 14 м, найдите угол, образуемый дугой.

Решение

Длина дуги = 2πr (θ / 360)

35 м = 2 x 3,14 x 14 x (θ / 360)

35 = 87,92θ / 360

Умножить обе стороны на 360 удалить дробь.

12600 = 87,92θ

Разделите обе стороны на 87,92

θ = 143,3 градуса.

Пример 4

Найдите радиус дуги длиной 156 см, переходящей под углом 150 градусов к центру круга.

Решение

Длина дуги = 2πr (θ / 360)

156 см = 2 x 3,14 xrx 150/360

156 = 2,6167 r

Разделите обе стороны на 2,6167

r = 59,62 см .

Итак, радиус дуги 59,62 см.

Как найти длину дуги в радианах?

Существует взаимосвязь между углом, образуемым дугой в радианах, и отношением длины дуги к радиусу окружности. В данном случае

θ = (длина дуги) / (радиус окружности).

Следовательно, длина дуги в радианах определяется выражением,

S = r θ

, где θ = угол между дугой в радианах

S = длина дуги.

r = радиус окружности.

Один радиан — это центральный угол, образованный дугой одного радиуса, то есть s = r

Радиан — это просто еще один способ измерения величины угла. Например, чтобы преобразовать углы из градусов в радианы, умножьте угол (в градусах) на π / 180.

Аналогичным образом, чтобы преобразовать радианы в градусы, умножьте угол (в радианах) на 180 / π.

Пример 5

Найдите длину дуги с радиусом 10 см и под углом 0,349 радиана.

Раствор

Длина дуги = r θ

= 0,349 x 10

= 3,49 см.

Пример 6

Найдите длину дуги в радианах с радиусом 10 м и углом 2.356 радиан.

Решение

Длина дуги = r θ

= 10 м x 2,356

= 23,56 м.

Пример 7

Найдите угол, образованный дугой длиной 10,05 мм и радиусом 8 мм.

Решение

Длина дуги = r θ

10,05 = 8 θ

Разделите обе стороны на 8.

1,2567 = θ

Здесь угол, образованный дугой, равен 1,2567 радиана.

Пример 8

Вычислите радиус круга, длина дуги которого составляет 144 ярда, а угол дуги равен 3.665 радиан.

Решение

Длина дуги = r θ

144 = 3,665r

Разделите обе стороны на 3,665.

144 / 3,665 = r

r = 39,29 ярда.

Пример 9

Вычислите длину дуги, которая образует угол 6,283 радиана с центром круга с радиусом 28 см.

Решение

Длина дуги = r θ

= 28 x 6,283

= 175.93 см

Малая дуга (h4)

Младшая дуга — это дуга, которая проходит под углом менее 180 градусов к центру окружности. Другими словами, малая дуга меньше полукруга и представлена ​​на окружности двумя точками. Например, дуга AB в окружности ниже — это второстепенная дуга.

Большая дуга (h4)

Большая дуга окружности — это дуга, которая проходит под углом более 180 градусов к центру окружности.Большая дуга больше полукруга и представлена ​​тремя точками на окружности.

Например, PQR — это большая дуга окружности, показанной ниже.

Практические задачи

1. Найдите площадь сектора окружности радиусом 9 мм. Предположим, что угол, образованный этой дугой в центре, равен 30 ^o .
2. Город A находится к северу от города B. Широты города A и города B составляют 54 ^o северной широты и 45 ^o северной широты, соответственно.Каково расстояние между двумя городами с севера на юг? Радиус Земли 6400 км.

Предыдущий урок | Главная страница | Следующий урок

Измерение дуги: определение и формула — видео и стенограмма урока

Измерение дуги в зависимости от длины дуги

Есть два разных способа идентифицировать дугу. Мы можем определить его по длине или по углу, который дуга образует в центре круга. Пролет дуги называется длиной дуги , а мера угла, который создает дуга, называется мерой дуги . Посмотрите на картинку ниже, которая иллюстрирует обе характеристики дуги:

Круговая дуга

Чтобы понять величину дуги, нам нужно знать величину угла как в градусах, так и в радианах. Давайте теперь немного поговорим о градусах и радианах и их соотношении.

Градусы и радианы

Углы имеют две разные единицы измерения. Круг измеряет 360 градусов.Степень угла будет представлять ту же часть круга, что и соответствующая дуга угла. Например, 90 градусов составляют 1/4 от 360 градусов, поэтому для угла 90 градусов соответствует дуга, составляющая 1/4 окружности.

Другая единица измерения, которую мы используем для измерения угла, — это радиан. Связь между радианами и градусами позволяет нам конвертировать между ними, используя следующие правила. Имейте в виду, что полный круг равен 360 градусам или 2 радианам на дюйм, а один радиан равен 180 градусам.

• Мера угла в градусах равна измерению угла в радианах: чтобы преобразовать градусы в радианы, мы умножаем градус на пи / 180.
• Мера угла в радианах равна величине угла в градусах: Чтобы преобразовать радианы в градусы, мы умножаем радиан на 180 / пи.

Например, давайте вычислим радиан для угла в 90 градусов.

• 90 умножить на пи / 180 = 90 (пи / 180).
• 90pi / 180 = пи / 2 радиана.

Таким образом, угол в 90 градусов имеет радианную меру пи / 2 радиана.

А теперь конвертируем радианы в градусы.

• Пи / 3, умноженное на 180 / пи = (пи / 3) (180 / пи).
• 180pi / 3pi = 180/3 = 60 градусов.

Формула измерения дуги

Знакомство с радианами важно при использовании формулы измерения дуги, которая требует знания длины дуги и радиуса окружности, которой принадлежит дуга. Согласно формуле, s / r , s представляет длину дуги, а r представляет радиус окружности

Чтобы проиллюстрировать эту формулу, давайте рассмотрим дугу, показанную на следующей диаграмме:

Диаграмма 1

Как видите, согласно рисунку длина дуги составляет 4 единицы, а радиус — 5 единиц. Помните, что формула для измерения дуги: s / r , или 4/5.

Теперь давайте преобразуем 4/5 радиан в градусы, умножив на 180 / пи.

• (4/5) (180 / пи) = 45,837, или приблизительно 46 градусов.
• Поскольку 46 градусов составляют примерно 1/8 от 360 градусов, дуга должна составлять примерно 1/8 окружности, как показано в нашем примере.

Резюме урока

Давайте сделаем несколько минут, чтобы повторить то, что мы узнали. Дуга — это отрезок окружности.Мера дуги — это мера угла, который дуга образует в центре окружности, а длина дуги — это длина дуги. Эта мера может быть выражена в градусах или радианах. Мы можем легко преобразовать между ними, используя тот факт, что пи радиан = 180 градусов. Чтобы преобразовать радианы в градусы, мы умножаем на 180 / пи. Чтобы преобразовать градусы в радианы, мы умножаем их на пи / 180. Зная длину дуги ( s ) и радиус ( r ) окружности, мы можем использовать формулу измерения дуги: s / r .

Дуга

Дуги часто изучаются в геометрии в контексте дуг окружности. На круге вы можете представить дугу как часть окружности круга, как показано на рисунке ниже.

Дуги также существуют как часть кривых, но в большинстве случаев, когда люди ссылаются на дугу, они обычно имеют в виду дугу окружности, а не дугу кривой. Точно так же эта страница будет посвящена теме дуг окружности.

Дуга от A до B, обозначенная символом как, показана выше красным цветом.

Дуги широко используются в машиностроении и других сферах быта. Показанный ниже мост имеет опоры в форме дуги.

Виды дуг

Полукруг — это название дуги, охватывающей половину окружности окружности (одно из значений полукруга — половина).

красным — полукруг для круга О.

Есть два других типа дуг: второстепенные и большие дуги. Вспомогательная дуга — это дуга, длина которой меньше длины полукруга.Большая дуга имеет длину дуги больше, чем у полукруга.

На рисунке ниже — вспомогательная дуга.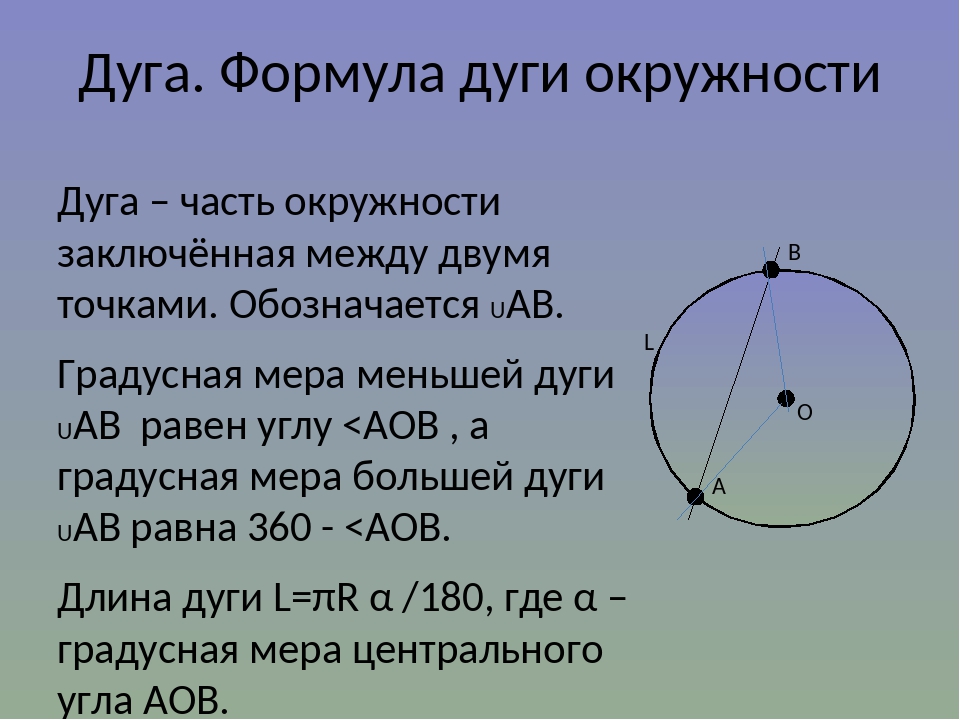 Второстепенные дуги обычно именуются только по их конечным точкам. это большая дуга. Главные дуги названы по их конечным точкам и некоторым другим точкам, лежащим на дуге.

Центральный угол

Центральный угол — это угол, вершиной которого является центр окружности. Когда концы дуги пересекают стороны центрального угла, мы говорим, что дуга образует угол.Размер дуги равен величине центрального угла, образуемого дугой.

расширяет ∠QPR так, что мера также равна θ.

Кроме того, поскольку длина окружности равна 360 °, мы можем найти меру большой дуги, найдя разность в 360 ° и меру малой дуги. Итак,

Сложение дуги

Дуга, образованная двумя соседними дугами, имеет меру, которая является суммой двух соседних дуг.

Углы и дуги прочие

Вписанный угол — это угол, образованный внутри круга, когда две хорды или секущие линии пересекаются на окружности.∠RSQ на рисунке ниже является примером. Размер вписанного угла составляет половину угла, образованного дугой. На рисунке ниже

Размер каждого угла, образованного двумя пересекающимися хордами внутри круга, составляет половину суммы дуг, соединяющих углы. На рисунке ниже

Угол, образованный двумя секущими, пересекающимися вне круга, составляет половину разности дуг, образующих угол, образованный секущими.На рисунке ниже

Длина дуги

Поскольку размер дуги равен величине ее центрального угла, мы можем определить длину дуги, используя отношение центрального угла дуги к 360 °. При длине дуги 60 ° соотношение будет (60 °) / (360 °) = 1/6. Итак, дуга составляет 1/6 длины окружности. Поскольку длина окружности равна 2πr, длина дуги равна.

Как правило, длина дуги, с, составляет:

где r — радиус окружности, а θ — угол в градусах.Если угол θ выражен в радианах, длина дуги составляет:

с = rθ

Пример:

См. Рисунок выше. Для окружности с радиусом 15 и θ = 120 ° найдите длину дуги s.

Другое применение дуг

Дуги также определены в контексте исчисления. Дуга — это часть дифференцируемой кривой. Один из способов подумать об этом без фона исчисления состоит в том, что в дифференцируемой кривой участок кривой не имеет разрывов в кривой, и что он гладкий и не имеет каких-либо «заостренных» участков, таких как V или функция абсолютного значения.

Дуга от A до B, показанная красным, является частью кривой.

Длина дуги — формула, как найти длину дуги, примеры

Длину дуги лучше определять как расстояние вдоль части окружности любого круга или любой кривой (дуги). Любое расстояние вдоль изогнутой линии, образующей дугу, называется длиной дуги. Часть кривой или часть окружности называется дугой. Все они имеют кривую форму. Длина дуги больше, чем любое расстояние по прямой между ее концами (хорда).

Что такое длина дуги?

Длина дуги определяется как промежуток между двумя точками на участке кривой. Дуга окружности — это любая часть окружности. Угол, образованный дугой в любой точке, — это угол, образованный между двумя отрезками линии, соединяющими эту точку с конечными точками дуги. Например, в круге, показанном ниже, OP — это дуга окружности с центром Q. Длина дуги OP задается как L.

Формула длины дуги

Длину дуги можно рассчитать по разным формулам, исходя из единицы измерения центрального угла дуги. Измерения центрального угла могут быть даны в градусах или радианах, и, соответственно, мы вычисляем длину дуги окружности. Для круга формула длины дуги равна θ, умноженному на радиус круга.

Формула длины дуги в радианах может быть выражена как длина дуги = θ × r, когда θ выражается в радианах.Длина дуги = θ × (π / 180) × r, где θ в градусах, где,

• L = длина дуги
• θ = Центральный угол дуги
• r = Радиус окружности

Формула длины дуги в радианах

Длину дуги окружности можно рассчитать по различным формулам, исходя из единицы измерения центрального угла дуги. Формула длины дуги в радианах может быть выражена как

.

Длина дуги = θ × r

где,

• L = Длина дуги
• θ = центральный угол дуги в радианах
• r = Радиус окружности

Как найти длину дуги кривой?

Длину дуги окружности можно рассчитать с помощью различных методов и формул на основе заданных данных. Некоторые важные случаи приведены ниже,

• найти длину дуги с радиусом и центральным углом
• найти длину дуги без радиуса
• найти длину дуги без центрального угла

Как найти длину дуги по радиусу и центральному углу?

Длину дуги окружности можно рассчитать по радиусу и центральному углу, используя формулу длины дуги,

• Длина дуги = θ × r, где θ в радианах.
• Длина дуги = θ × (π / 180) × r, где θ в градусах.

Как найти длину дуги без радиуса?

Длину дуги окружности можно рассчитать без радиуса с помощью:

Центральный угол и площадь сектора:

• Умножьте площадь сектора на 2 и разделите результат на центральный угол в радианах.
• Найдите квадратный корень из результата деления.
• Умножьте полученный корень еще раз на центральный угол, чтобы получить длину дуги.
• Единицами этой вычисленной длины дуги будет квадратный корень из единиц площади сектора.

Пример: вычислить длину дуги кривой с площадью сектора 25 квадратных единиц и центральным углом как 2 радиана.

У нас,

Площадь сектора = 25 шт.

Центральный угол = 2 радиана

• Шаг 1: Площадь сектора × 2 = 25 × 2 = 50
• Шаг 2: 50 / центральный угол = 50/2 = 25
• Шаг 3: √25 = 5
• Шаг 4: 5 × центральный угол = 5 × 2 = 10 единиц

Таким образом, длина дуги = 10 шт.

Центральный угол и длина хорды:

• Разделите центральный угол в радианах на 2 и выполните над ним синусоидальную функцию.
• Разделите полученную длину хорды вдвое на результат шага 1. Этот расчет дает вам в качестве результата радиус.
• Умножьте радиус на центральный угол, чтобы получить длину дуги.

Пример : Рассчитайте длину дуги кривой, конечные точки которой касаются хорды окружности размером 5 единиц. Центральный угол, образованный дугой, составляет 2 радиана.

У нас,

Длина хорды = 5 единиц

Центральный угол = 2 радиана

• Шаг 1: Центральный угол / 2 = 2/2 = 1
• Шаг 2: Sin (1) = 0.841
• Шаг 3: Длина хорды / (2 × 0,841) = 5 / 1,682 = 2,973 единиц = радиус
• Шаг 4: Длина дуги = радиус × центральный угол = 2,973 × 2 = 5,946 единиц

Таким образом, длина дуги = 5,946 ед.

Как найти длину дуги без центрального угла?

Длину дуги окружности можно рассчитать без угла по формуле:

Радиус и площадь сектора :

• Умножьте площадь сектора на 2.
• Затем разделите результат на квадрат радиуса (единицы должны быть одинаковыми), чтобы получить центральный угол в радианах.
• Умножьте центральный угол на радиус, чтобы получить длину дуги.

Пример: вычислить длину дуги кривой с площадью сектора 25 квадратных единиц и радиусом как 2 единицы.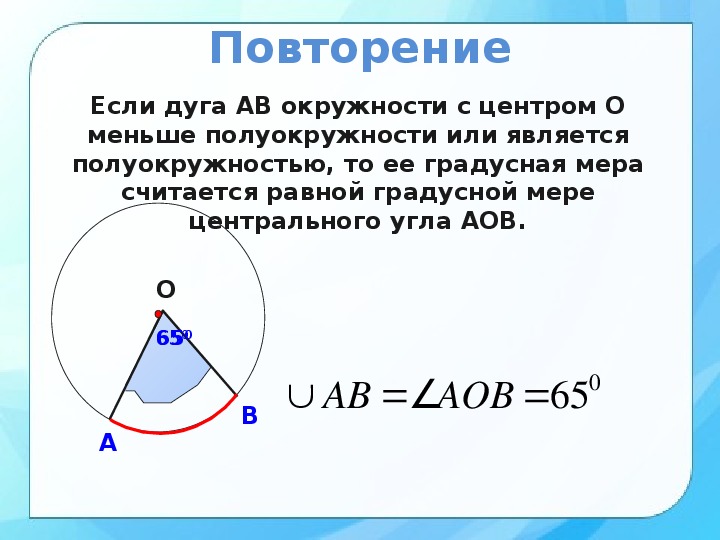

У нас,

Площадь сектора = 25 шт.

Центральный угол = 2 шт.

• Шаг 1: Площадь сектора × 2 = 25 × 2 = 50
• Шаг 2: 50 / радиус ² = 50/4 = 12.5 = центральный угол (рад)
• Шаг 3: Длина дуги = радиус × центральный угол = 2 × 12,5 = 25 единиц

Таким образом, длина дуги = 25 ед.

Радиус и длина хорды:

• Разделите длину хорды на удвоенный заданный радиус.
• Найдите обратный синус полученного результата.
• Удвойте результат обратного синуса, чтобы получить центральный угол в радианах.
• Умножьте центральный угол на радиус, чтобы получить длину дуги.

Пример : Рассчитайте длину дуги кривой, конечные точки которой касаются хорды окружности размером 5 единиц. Радиус круга — 2 единицы.

У нас,

Длина хорды = 5 единиц

Центральный угол = 2 шт.

• Шаг 1: Длина хорды / (2 × радиус) = 5 / (2 × 2) = 1,25
• Шаг 2: Sin ^-1 (1,25) = 0,949
• Шаг 3: Центральный угол = 2 × 0.949 = 1,898 радиан
• Шаг 4: Длина дуги = радиус × центральный угол = 2 × 1,898 = 3,796 единиц

Таким образом, длина дуги = 3,796 ед.

☛ Важные примечания относительно длины дуги

Ниже приведены основные моменты концепции длины дуги.

• Длина дуги = θ × r, где θ в радианах.
• Длина дуги = θ × (π / 180) × r, где θ в градусах.

☛ Связанные темы по длине дуги

Ознакомьтесь с еще несколькими интересными статьями, посвященными длине дуги, чтобы лучше понять тему.

Часто задаваемые вопросы о длине дуги

Какова длина дуги окружности?

Длина дуги окружности определяется как промежуток между двумя точками на участке кривой. Дуга окружности — это любая часть окружности. Угол, образованный дугой в любой точке, — это угол, образованный между двумя отрезками линии, соединяющими эту точку с конечными точками дуги.

Как найти длину дуги без радиуса?

Длину дуги окружности можно рассчитать без радиуса с помощью:

Центральный угол и площадь сектора:

• Умножьте площадь сектора на 2 и разделите результат на центральный угол в радианах.
• Найдите квадратный корень из результата деления.
• Умножьте полученный корень еще раз на центральный угол, чтобы получить длину дуги.
• Единицами этой вычисленной длины дуги будет квадратный корень из единиц площади сектора.

Центральный угол и длина хорды:

• Разделите центральный угол в радианах на 2 и выполните над ним синусоидальную функцию.
• Разделите длину хорды вдвое на результат шага 1.Этот расчет дает вам в результате радиус.
• Умножьте радиус на центральный угол, чтобы получить длину дуги.

Что вы понимаете под уравнением длины дуги?

Есть два уравнения, связанных с длиной дуги. Ниже приведены два уравнения длины дуги.

• Длина дуги = θ × r, где θ в радианах.
• Длина дуги = θ × (π / 180) × r, где θ в градусах

Как определить длину дуги с помощью радианов?

Длину дуги можно рассчитать, если центральный угол задается в радианах по формуле: Длина дуги = θ × r, когда θ выражается в радианах.

• L = Длина дуги
• θ = центральный угол дуги
• r = Радиус окружности

Должна ли длина дуги быть в радианах?

Нет, длина дуги не может быть указана в радианах. Это измерение расстояния, поэтому не может быть в радианах. Центральный угол в центре может быть в радианах, градусах или угловых секундах соответственно.

Как определить длину окружности дуги?

Когда длина дуги задается с центральным углом θ, тогда длина окружности рассчитывается как длина дуги (L) / окружность = θ / 360º.

Какова длина большой дуги по формуле длины дуги?

Большая дуга в окружности больше полукруга. По измерениям он превышает 180 °. Используя формулу ℓ = rθ, мы можем найти длину дуги окружности, где θ в радианах.

Длина дуги — Концепция — Геометрия Видео от Brightstorm

Обычно путают с мерой дуги, длина дуги — это расстояние между конечными точками по окружности.Измерение дуги — это измерение в градусах, равное центральному углу, образующему перехваченную дугу. Длина дуги — это часть длины окружности, которая рассчитывается таким образом: найдите длину окружности и умножьте ее на длину дуги, разделенную на 360.

Когда мы говорим о кругах, есть два свойства, которые легко спутать. Длина дуги в зависимости от длины дуги.Чтобы сравнить длину дуги и ее размер, давайте посмотрим на несколько концентрических окружностей. Допустим, я нарисовал 2 радиуса в меньшем круге, и я назвал эту перехваченную дугу, дугой a, скажем, я расширил эти радиусы полностью до большего круга, и я собираюсь называть это дугой b, так что мы снова пытаемся сравнить меру дуги с длиной дуги, и я вижу, что, поскольку она имеет одинаковый центральный угол, поскольку дуга a и дуга b имеют одинаковый центральный угол, я мог бы сказать, что мера, мера дуги a равна мере из б.Но если мы посмотрим на расстояние между конечными точками перехваченных дуг, мы можем довольно ясно увидеть, что длина l, e, n, g, t, h дуги a определенно меньше, чем длина b, поэтому это возможно для двух дуг. иметь одинаковую меру, но разную длину.
Длина дуги — это часть окружности круга, поэтому, если мы посмотрим на круг здесь, где я нарисовал прямой угол и сказал, какое расстояние между x и y? Если мы знаем, что весь круг имеет окружность c, где c — некоторая длина окружности, мы знаем, что дробь здесь, это довольно ясно, будет просто четвертью от этого, потому что 90 градусов — это одна четверть круга, поэтому круг равен 360, 90 составляет одну четверть, поэтому мы рассчитываем длину дуги, если у меня есть круг с дугой ab, длина которой равна длине окружности всего круга, умноженной на долю круга, поэтому эта часть прямо здесь говорит вам, если вы знать меру дуги ab, просто запишите ее на 360, и вы узнаете, какую часть круга вы используете? Таким образом, вместо c вы можете либо заменить 2 pi r, потому что эта окружность с точки зрения радиуса равна мере дуги ab из 360, либо, если хотите, вы также можете использовать число пи, умноженное на диаметр, умноженное на длину дуги ab из 360. Таким образом, ключевым моментом здесь является то, что длина дуги — это часть окружности круга, поэтому мы говорим о расстоянии, поэтому у вас может быть одна и та же длина дуги, но разные длины дуги.

секторов, областей и дуг | Purplemath

Purplemath

Как вы помните из геометрии, задается площадь A окружности с радиусом длины r :

Окружность C (то есть длина по внешней стороне) того же круга определяется как:

Эти формулы дают нам площадь и длину дуги (то есть длину «дуги» или изогнутой линии) для всей окружности .Но иногда нам нужно работать только с частью оборота круга или со многими оборотами круга. Какие формулы мы тогда используем?

MathHelp.

com

Если мы начнем с круга с обозначенной радиусной линией и немного повернем круг, то выделенная область будет выглядеть как кусок пирога или кусок пиццы; это называется «сектором» круга, и этот сектор выглядит как зеленая часть этого изображения:

Угол, отмеченный исходным и конечным местоположениями радиусной линии (то есть угол в центре пирога / пиццы), является «вытянутым» углом сектора.Этот угол также можно назвать «центральным» углом сектора. На картинке выше центральный угол обозначен как «θ» (произносится как «THAY-tuh»).

---

Филиал

---

Какова площадь A сектора, ограниченного отмеченным центральным углом θ? Какова длина дуги s , являющейся частью окружности, образуемой этим углом?

Чтобы определить эти значения, давайте сначала внимательно рассмотрим формулы площади и окружности. Площадь и длина окружности указаны для всего круга, что составляет один полный оборот радиусной линии. Подложенный угол для «одного полного оборота» равен 2π. Таким образом, формулы для площади и окружности всего круга можно переформулировать как:

Каков смысл разбиения значения угла «один раз по кругу»? Я сделал это, чтобы подчеркнуть, как угол для всего круга (равный 2π) вписывается в формулы для всего круга.Затем это позволяет нам точно увидеть, как и где предполагаемый угол θ сектора будет вписываться в формулы сектора. Теперь мы можем заменить угол «один раз вокруг» (то есть 2π) для всей окружности мерой угла наклона сектора θ, и это даст нам формулы для площади и длины дуги этого сектора:

Примечание. Если вы работаете с углами, измеряемыми в градусах, а не в радианах, вам необходимо включить дополнительный коэффициент преобразования:

.

Признание: Большая часть причины, по которой я объяснил взаимосвязь между формулами круга и формулами секторов, заключается в том, что я никогда не мог отслеживать формулы площади сектора и длины дуги; Я всегда их забывала или портила.Но я всегда мог вспомнить формулы для площади и окружности всего круга. Таким образом, я узнал (на собственном горьком опыте), что, помня о вышеупомянутой взаимосвязи, отмечая, где идут углы в формулах для полного круга, всегда можно сохранить прямую форму.

• Дан окружность радиусом

  r = 8 единиц и сектор с выступом под углом 45 °, найдите площадь сектора и длину дуги.

Мне дали радиус и центральный угол, так что я могу просто ввести формулы и упростить получение ответов. Для удобства я сначала конвертирую «45 °» в соответствующее значение

π / 4 в радианах. Затем я сделаю свой плагин:

Тогда мой ответ:

площадь A = 8π квадратных единиц, длина дуги с = 2π единиц

Обратите внимание, как я добавляю «единицы» в свои ответы.Если бы они указали конкретную единицу измерения радиуса, например «сантиметры» или «мили» или что-то еще, то я мог бы дать более конкретный ответ. Как бы то ни было, я должен был быть универсальным.

Часто, если в вопросе не указывается единица или просто говорится «единицы», вы, вероятно, можете уйти, не добавляя «единицы» в свой ответ. Однако это часто приводит к плохой привычке полностью игнорировать юниты, а потом — сюрприз! — инструктор считает на тесте, потому что вы не включили никаких единиц.Вероятно, лучше проявить осторожность и всегда указывать или единиц, даже если это просто «единицы», в своих ответах.

---

• Дан сектор с радиусом

  r = 3 см и соответствующей длиной дуги 5π радиан, найдите площадь сектора.

Для этого упражнения мне дали радиус и длину дуги. Чтобы найти площадь сектора, мне нужно измерить центральный угол, который мне дали , а не .Однако в формулу длины дуги входит центральный угол. Итак, я могу подставить радиус и длину дуги в формулу длины дуги и найти меру приложенного угла. Как только у меня это получится, я могу быстро найти область сектора.

Таким образом, центральный угол этого сектора составляет

(5/3) π. Тогда площадь сектора равна:

И это значение — числовая часть моего ответа.Поскольку это значение обозначает «площадь», то есть квадратное измерение, я хочу не забыть поставить «квадрат» на единицы, которые они дали мне для радиуса.

см ²

Иногда упражнение дает вам информацию, но, как и выше, может показаться, что это не та информация, которая вам действительно нужна. Не бойтесь возиться со значениями и формулами; попытайтесь выяснить, сможете ли вы найти черный ход к решению или какую-нибудь другую манипуляцию, которая даст вам то, в чем вы нуждаетесь.Это нормально не знать в самом начале, как вы собираетесь дойти до конца. (И, если они сообщат вам или попросят диаметр, помните, что радиус составляет половину диаметра, а диаметр — в два раза больше радиуса.)

---

• Сектор круга имеет площадь 108 см

  ² , а сектор пересекает дугу длиной 12 см. Найдите диаметр круга.

У меня спросили диаметр.В формулах, которые я узнал, используется радиус. Но я могу найти радиус, а затем удвоить его, чтобы получить диаметр, так что это не проблема. Однако они попросили меня указать длину, учитывая длину дуги и площадь, каждая из которых использует радиус и предполагаемый угол. И у меня нет ни одной из этих ценностей. Так что же мне делать?

Когда я не могу придумать, чем еще заняться, я включаю все, что они мне дали, в любые формулы, которые могут иметь отношение, и я надеюсь, что из этого выпадет что-то, что я смогу использовать.Итак:

A = (θ / 2) r ² = 108

с = θ r = 12

Я могу заменить из второй строки выше на первую строку выше (после некоторой перестановки) и посмотреть, поможет ли мне результат вообще:

(θ / 2) r ² = 108

(1/2) [θ r ] r = 108

(1/2) [12] r = 108

r = 18

га! Я нашел значение радиуса! У меня нет значения центрального угла, но они этого не просили, и, оказывается, мне это все равно не понадобилось. Они спросили меня о диаметре, который в два раза больше радиуса, поэтому мой ответ (включая единицы измерения!):

---

URL: https://www.purplemath.com/modules/sectors.htm

Формула измерения дуги

| Как найти угол дуги (видео)

Определение измерения дуги

Дуга — это отрезок окружности по окружности.Измерение дуги — это угол, который дуга образует в центре окружности, а длина дуги — это промежуток вдоль дуги. Эта угловая мера может быть в радианах или градусах, и мы можем легко преобразовать их по формуле π радиан = 180 °.

Вы также можете измерить окружности , или расстояние вокруг окружности. Если вы возьмете меньше полной длины окружности, ограниченной двумя радиусами, у вас будет дуга . Этот изогнутый кусок круга и внутреннего пространства называется сектором , как кусок пиццы. Когда вы разрезаете круговую пиццу, корочка разделяется на дуги.

1. Определение измерения дуги
2. Круговая дуга
3. Измерение длины дуги в зависимости от длины дуги
4. Градусы и радианы
5. Формула измерения дуги
6. Как найти длину дуги
7. Как найти длину дуги
8. Определение угла дуги

Круговая дуга

Если разрезать вкусную свежую пиццу, мы получим две половинки, каждая из которых представляет собой дугу размером 180 °.Если мы сделаем три дополнительных разреза только на одной стороне (таким образом, мы разрезаем половину сначала на две четверти, а затем каждую четверть на две восьмых), у нас будет одна сторона пиццы с одной большой дугой 180 °, а другая сторона пицца с четырьмя дугами 45 °, как это:

Половина пиццы, представляющая собой один гигантский кусок, представляет собой большую дугу , поскольку ее размер составляет 180 ° (или больше). На другой стороне пиццы есть четыре второстепенных дуги , так как каждая из них имеет угол менее 180 °.

Измерение дуги в зависимости от длины дуги

Дуга — это часть длины окружности, которая лежит между двумя точками на окружности. Дуга имеет два измерения:

1. Длина дуги — это расстояние по окружности, измеряемое в тех же единицах, что и радиус, диаметр или полная длина окружности; это будут линейные единицы измерения, такие как дюймы, см, м, ярды и т. д.
   
2. Измерение угла дуги , сделанное в центре окружности, частью которой является дуга, измеряется в градусах (или радианах)
   

Не путайте измерение дуги (длины или угла) с расстоянием по прямой линии хорды , соединяющей две точки дуги на окружности.Длина хорды будет , всегда короче длины дуги.

градусов и радианов

Чтобы вычислить величину дуги, вам необходимо понимать, как измеряются углы как в градусах, так и в радианах. Угол измеряется в градусах или радианах. Круг измеряет 360 градусов или 2π радиан, тогда как один радиан равен 180 градусам . Таким образом, градусы и радианы связаны следующими уравнениями:

360 ° = 2π радиан

180 ° = π радиан

Связь между радианами и градусами позволяет нам преобразовывать друг друга с помощью простых формул.Чтобы преобразовать градусы в радианы, мы берем меру градуса, умноженную на число пи, деленное на 180.

Давайте переведем 90 градусов в радианы, например:

90 ° × π180 °

90π180

π2 радиан

Теперь конвертируем π3 радиан в градусы:

π3 × 180π

180π3π

1803 = 60 °

Формула измерения дуги

Как только вы освоите радианы, мы можем использовать формулу измерения дуги, которая требует для вычисления длины дуги s и радиуса окружности r.

мера дуги = длина дуги радиус = sr

Как найти длину дуги

Давайте попробуем пример, где длина нашей дуги составляет 3 см, а радиус — 4 см, как показано на нашей иллюстрации:

Начните с нашей формулы и включите все, что мы знаем:

мера дуги = sr

мера дуги = 34

Теперь мы можем преобразовать 34 радиана в градусы, умножив на 180 и разделив на π.

34180π

42.9718 ≈ 43 °

Как найти длину дуги

Чтобы рассчитать длину дуги, вам необходимо знать размер центрального угла, образовавшего дугу (угол двух радиусов).Длина дуги — это дробная часть длины окружности круга. Длина окружности любого круга находится с 2πr, где r = радиус. Если у вас есть диаметр, вы также можете использовать πd, где d = диаметр.

Формула для определения длины дуги:

Длина дуги = угол дуги 360 ° 2πr

Давайте попробуем пример с этой пиццей:

Наш пирог имеет диаметр 16 дюймов, что дает радиус 8 дюймов. Мы знаем, что угол среза составляет 60 °. Итак, формула для этого конкретного кусочка пиццы:

.

= 60 ° 360 ° · 2 · π · 8

= 16 · 16π

≈ 8.3775 «

Определение указанного угла дуги

Измерение угла дуги отображается как mAB⌢, где A и B — две точки на окружности, образующей дугу. Буква m означает измерение, а короткая изогнутая линия над AB⌢ указывает на то, что мы имеем в виду дугу. Две точки получены из центрального угла (угла двух радиусов, выходящих из центральной точки).

Одно важное различие между длиной дуги и углом дуги состоит в том, что для двух окружностей разного диаметра секторы с одинаковым углом из каждой окружности не будут иметь одинаковую длину дуги.Длина дуги изменяется в зависимости от радиуса или диаметра круга (или пиццы).

Краткое содержание урока

Теперь, когда вы освоили этот урок, вы можете идентифицировать и определять дугу, а также различать большие и второстепенные дуги. Вы также можете измерить дугу в линейных единицах и градусах и использовать правильный символ mAB⌢ (где A и B — две точки на окружности), чтобы показать длину дуги.

Следующий урок:

По касательной к окружности

.