принцип работы, схема и уравнение

В данной статье мы подробно разберем осциллятор и принцип его работы, а так же разберем схемы, резонанс осциллятора, затухающие колебания и резонансную частоту.

Описание и принцип работы

Осцилляторы преобразуют вход постоянного тока (напряжение питания) в выход переменного тока (форму волны), который может иметь широкий диапазон различных форм и частот, которые могут быть либо сложными по своей природе, либо простыми синусоидальными волнами в зависимости от применения.

Осцилляторы также используются во многих испытательных приборах, генерирующих синусоидальные, квадратные, пилообразные или треугольной формы волны или просто последовательность импульсов переменной или постоянной ширины. Осцилляторы LC обычно используются в радиочастотных цепях из-за их хороших характеристик фазового шума и простоты их реализации.

Осциллятор является в основном усилителем с «положительной обратной связью», или регенеративной обратной связью (в фазе) и одной из многих проблем в конструкции электронных схем является прекращение генерации усилителей при попытке заставить осциллятор колебаться.

Осцилляторы работают, потому что они преодолевают потери своей резонансной цепи обратной связи либо в виде конденсатора, индуктора или обоих в одной и той же цепи, подавая энергию постоянного тока с требуемой частотой в эту резонаторную цепь. Другими словами, осциллятор представляет собой усилитель, который использует положительную обратную связь, которая генерирует выходную частоту без использования входного сигнала.

Таким образом, осцилляторы являются самоподдерживающимися цепями, генерирующими периодическую форму выходного сигнала с точной частотой, и для того, чтобы любая электронная схема работала в качестве осциллятора, она должна иметь следующие три характеристики.

• Некоторая форма усиления
• Положительная обратная связь (регенерация)
• Частота определения обратной связи сети

Осциллятор имеет небольшой усилитель с обратной связью по сигналу с коэффициентом усиления разомкнутого контура, равным или немного превышающим единицу для запуска колебаний, но для продолжения колебаний средний коэффициент усиления контура должен возвращаться к единице. В дополнение к этим реактивным компонентам требуется усилительное устройство, такое как операционный усилитель или биполярный транзистор.

В отличие от усилителя, для работы осциллятора не требуется внешний вход переменного тока, так как энергия источника постоянного тока преобразуется осциллятором в энергию переменного тока на необходимой частоте.

Базовая цепь обратной связи осциллятора

Где: 
β — доля обратной связи.

Осциллятор усиления без обратной связи

Осциллятор с обратной связью

Осцилляторы — это схемы, которые генерируют непрерывный выходной сигнал напряжения на требуемой частоте со значениями индукторов, конденсаторов или резисторов, образующих частотно-избирательный LC-резонансный контур емкости и сеть обратной связи. Эта сеть обратной связи является сетью ослабления, которая имеет коэффициент усиления меньше единицы ( β <1 ) и запускает колебания, когда Aβ> 1, который возвращается к единице ( Aβ = 1 ) после начала колебаний.

Частота генераторов LC контролируется с использованием настроенной или резонансной индуктивно-емкостной (LC) цепи, а результирующая выходная частота называется частотой колебаний. Делая обратную связь осцилляторов реактивной сетью, фазовый угол обратной связи будет изменяться как функция частоты, и это называется фазовым сдвигом.

Есть в основные типы осцилляторов:

• 1. Синусоидальные осцилляторы   — они известны как гармонические осцилляторы и обычно представляют собой осциллятор типа «LC Tuned-feedback» или «RC-Tuned-Feedback», который генерирует чисто синусоидальный сигнал с постоянной амплитудой и частотой.
• 2. Несинусоидальные осцилляторы   — они известны как осцилляторы релаксации и генерируют сложные несинусоидальные сигналы, которые очень быстро меняются от одного состояния устойчивости к другому, например, «прямоугольная волна», «треугольная волна» или «пилообразная волна» формы сигналов.

Резонанс осциллятора

Когда к цепи, состоящей из индуктора, конденсатора и резистора, приложено постоянное напряжение, но переменной частоты, реактивное сопротивление цепей конденсатора / резистора и индуктора / резистора должно изменять как амплитуду, так и фазу выходного сигнала по сравнению с входным сигналом из-за реактивного сопротивления используемых компонентов.

На высоких частотах реактивное сопротивление конденсатора очень низкое, действуя как короткое замыкание, в то время как реактивное сопротивление индуктора высокое, действующее как разомкнутая цепь. На низких частотах верно обратное, реактивное сопротивление конденсатора действует как разомкнутая цепь, а реактивное сопротивление индуктора действует как короткое замыкание.

Между этими двумя крайностями комбинация индуктивности и конденсатора создает «настроенную» или «резонансную» цепь, которая имеет резонансную частоту ( ƒr ), в которой емкостное и индуктивное реактивные сопротивления равны и взаимно компенсируются, оставляя только сопротивление схема противодействия потоку тока. Это означает, что фазовый сдвиг отсутствует, поскольку ток находится в фазе с напряжением. Рассмотрим схему ниже.

Базовая схема осциллятора LC

Цепь состоит из индукционной катушки L и конденсатора C. Конденсатор накапливает энергию в форме электростатического поля и создает потенциал ( статическое напряжение ) на своих пластинах, в то время как индуктивная катушка накапливает энергию в форме электромагнитного поля. Конденсатор заряжается до напряжения питания постоянного тока V, поставив переключатель в положение A. Когда конденсатор полностью заряжен изменения переключателя в положение B.

Заряженный конденсатор теперь подключен параллельно через индуктивную катушку, поэтому конденсатор начинает саморазряжаться через катушку. Напряжение на C начинает падать, когда ток через катушку начинает расти.

Этот возрастающий ток создает электромагнитное поле вокруг катушки, которое сопротивляется этому потоку тока. Когда на конденсаторе C полностью разряжается энергия, которая была первоначально сохранена в конденсаторе C в качестве электростатического поля теперь сохраняется в индуктивной катушке L в виде электромагнитного поля вокруг обмоток катушек.

Поскольку в цепи теперь нет внешнего напряжения для поддержания тока внутри катушки, оно начинает падать, когда электромагнитное поле начинает разрушаться. В катушке индуцируется обратная ЭДС ( e = -Ldi / dt ), сохраняя ток в первоначальном направлении.

Этот ток заряжает конденсатор C с полярностью, противоположной его первоначальному заряду. C продолжает заряжаться до тех пор, пока ток не уменьшится до нуля и электромагнитное поле катушки полностью не исчезнет.

Энергия, первоначально введенная в цепь через переключатель, была возвращена конденсатору, который снова имеет потенциал электростатического напряжения на нем, хотя теперь он имеет противоположную полярность. Теперь конденсатор снова начинает разряжаться через катушку, и весь процесс повторяется. Полярность напряжения изменяется по мере того, как энергия передается туда-сюда между конденсатором и индуктором, создавая синусоидальное напряжение переменного тока и форму волны тока.

Этот процесс затем формирует основу цепи резервуара осцилляторов LC, и теоретически эта циклическая перемотка будет продолжаться бесконечно. Тем не менее, все не идеально, и каждый раз, когда энергия передается от конденсатора C к катушке индуктивности L и обратно от L к C, происходят потери энергии, которые со временем затухают колебания до нуля.

Это колебательное действие по передаче энергии назад и вперед между конденсатором C и катушкой индуктивности L будет продолжаться бесконечно, если бы не потери энергии в цепи. Электрическая энергия теряется в постоянном или реальном сопротивлении катушки индуктивности, в диэлектрике конденсатора и в излучении цепи, поэтому колебания неуклонно уменьшаются, пока они полностью не затухнут и процесс не остановится.

Затем в практической LC— схеме амплитуда колебательного напряжения уменьшается на каждом полупериоде колебаний и в конечном итоге затухает до нуля. Затем говорят, что колебания «демпфируются», причем величина демпфирования определяется качеством или добротностью цепи.

Затухающие колебания

Частота колебательного напряжения зависит от значения индуктивности и емкости в цепи LC — бака. Теперь мы знаем, что для возникновения резонанса в контуре резервуара должна быть точка частоты, где значение X _C емкостное сопротивление совпадает со значением X _L индуктивного сопротивления ( X _L  = X _C ) и что, следовательно, компенсирует друг друга, оставляя только постоянное сопротивление в цепи, чтобы противостоять потоку тока.

Если теперь мы поместим кривую для индуктивного реактивного сопротивления индуктора поверх кривой для емкостного реактивного сопротивления конденсатора так, чтобы обе кривые были на одной оси частот, точка пересечения даст нам точку резонансной частоты, (  ƒ _r или ωr  ), как показано ниже.

Резонансная частота

Где: 
ƒ _r в Герцах,
L в Генри и 
C в Фарадах

Тогда частота, с которой это произойдет, определяется как:

Затем за счет упрощения приведенного выше уравнения, мы получаем окончательное уравнение для резонансной частоты ƒ _г в настроенном LC цепи, как:

Где: L индуктивность в Генри
C — емкость в Фарадах
ƒ _r — выходная частота в Герцах

Это уравнение показывает, что если L или C уменьшаются, частота увеличивается. Эта выходная частота обычно дается сокращенная (  ƒ _г  ) , чтобы определить его как «резонансную частоту».

Чтобы сохранить колебания в цепи резервуара LC, мы должны заменить всю энергию, потерянную в каждом колебании, а также поддерживать амплитуду этих колебаний на постоянном уровне. Следовательно, количество заменяемой энергии должно быть равно энергии, потерянной в течение каждого цикла.

Если замещаемая энергия слишком велика, амплитуда будет увеличиваться до тех пор, пока не произойдет ограничение питающих шин. В качестве альтернативы, если количество заменяемой энергии слишком мало, амплитуда в конечном итоге со временем уменьшится до нуля, и колебания прекратятся.

Самый простой способ восполнить эту потерянную энергию — это взять часть выходного сигнала из цепи резервуара LC , усилить его и затем снова подать обратно в цепь LC . Этот процесс может быть достигнут с использованием усилителя напряжения с использованием операционного усилителя, полевого транзистора или биполярного транзистора в качестве активного устройства. Однако, если усиление контура усилителя обратной связи слишком мало, требуемое колебание уменьшается до нуля, а если оно слишком велико, форма сигнала искажается.

Чтобы производить постоянные колебания, уровень энергии, возвращаемой обратно в сеть LC, должен точно контролироваться. Тогда должна быть некоторая форма автоматической амплитуды или получить контроль, когда амплитуда пытается отличаться от опорного напряжения либо вверх, либо вниз.

Для поддержания стабильных колебаний общий коэффициент усиления цепи должен быть равен единице. Меньше, и колебания не начнутся или не угаснут до нуля, колебания больше не будут происходить, но амплитуда будет ограничена питающими рельсами, вызывая искажения. Рассмотрим схему ниже.

Базовая транзисторная схема осциллятора LC

В качестве усилителя LC-генератора используется биполярный транзистор, а настроенная схема LC- бака действует как нагрузка коллектора. Еще одна катушка L2 соединена между базой и эмиттером транзистора, чье электромагнитное поле «взаимно» в сочетании с этим катушки L.

«Взаимная индуктивность» существует между двумя цепями, и изменяющийся ток, протекающий в одной цепи катушки, посредством электромагнитной индукции индуцирует потенциальное напряжение в другой (эффект трансформатора), так что при возникновении колебаний в настроенной цепи электромагнитная энергия передается от катушки L на катушку L2, и напряжение базы той же частоты, что и в настроенной цепи, подается между базой и эмиттером транзистора. Таким образом, необходимое усилие автоматической обратной связи подается на усилительный транзистор.

Величина обратной связи может быть увеличена или уменьшена путем изменения связи между двумя катушками L и L2 . Когда цепь осциллирующая его импеданс резистивные и коллектор и база напряжение 180^o по фазе. Чтобы поддерживать колебания (называемые стабильностью частоты), напряжение, подаваемое на настроенную цепь, должно быть «синфазным» с колебаниями, возникающими в настроенной цепи.

Таким образом, мы должны ввести дополнительный 180 ^о фазовом сдвиге в цепь обратной связи между коллектором и базой. Это достигается путем намотки катушки L2 в правильном направлении относительно катушки L, что дает нам правильные соотношения амплитуды и фазы для цепи осцилляторов, или путем подключения сети фазового сдвига между выходом и входом усилителя.

Таким образом, LC-осциллятор представляет собой «Синусоидальный генератор» или «Гармонический генератор», как его чаще называют. Осцилляторы LC могут генерировать высокочастотные синусоидальные волны для использования в радиочастотных (РЧ) типов с транзисторным усилителем, состоящим из биполярного транзистора или полевого транзистора.

Гармонические осцилляторы бывают разных форм, потому что есть много различных способов построить сеть LC фильтра и усилитель с наиболее распространенными из которых являются в осциллятор Хартли LC , Колпитс LC осциллятор, Armstrong осциллятор и Clapp осциллятор.

Резюме осцилляторов LC

Основные условия, необходимые для резонансного контура резервуара осциллятора LC, приведены ниже.

• Чтобы колебания существовали, схема генератора ДОЛЖНА содержать реактивный (зависящий от частоты) компонент либо «Индуктор», ( L ) или «Конденсатор», ( С ), а также источник питания постоянного тока.
• В простой индуктивно-конденсаторной цепи LC колебания со временем затухают из-за потерь компонентов и цепей.
• Усиление напряжения требуется для преодоления этих потерь в цепи и обеспечения положительного усиления.
• Общее усиление усилителя должно быть больше единицы.
• Колебания могут поддерживаться путем подачи некоторого выходного напряжения в настроенную цепь, которая имеет правильную амплитуду и синфазный сигнал (0 ^o ).
• Колебания могут возникать только тогда, когда обратная связь является «положительной» (самовосстановление).
• Общий фазовый сдвиг цепи должен быть нулевым или 360 ^o, чтобы выходной сигнал из сети обратной связи был «синфазным» с входным сигналом.

В следующем уроке об осцилляторах мы рассмотрим работу одной из наиболее распространенных контуров LC-осциллятора, в которой используются две катушки индуктивности для формирования индуктивности с центральным постукиванием в его резонансной цепи бака. Этот тип схемы LC генератора известен как генератор Hartley.

это что такое? Принцип работы осциллятора

Осциллятор – это сварочное приспособление, которое облегчает проведение соответствующих работ с элементами из алюминия, другого цветмета и нержавейки. Подобное устройство помогает эффективно выполнить поджог сварочной дуги и поддержать ее стабильность. Прибор имеет как производственное, так и бытовое применение.

Как устроен агрегат?

Осциллятор, принцип работы которого заключается в формировании высокочастотным трансформатором подзарядки конденсатора и поддержании дальнейшей конкретной величины дуги, состоит из следующих элементов:

• Повышающего низкочастотного трансформатора (ПТ), обладающего вторичным напряжением 2-3 кВт.
• Разрядника (передаточного устройства).
• Индуктивного контура колебаний.
• Рабочей емкости.
• Блокирующего конденсатора.
• Предохранительной обмотки.

Через последний элемент конденсатор колебания высокой частоты прикасается к дуговому образованию. В нем напряжение источника питания не подвержено шунтированию. Дроссель, взаимодействующий с рабочей цепью, выполняет роль изолятора обмотки в аппарате от пробоя. Чаще всего используются варочные осцилляторы, мощность которых составляет 250-300 Вт. На продолжительность импульсов хватает буквально десятой доли секунды.

Импульсные приборы

Осциллятор – это устройство, которое подразделено на два типа. Прибор с импульсным питанием позволяет спровоцировать на начальном возникновении дуги ее постоянство при переменном токе. При выполнении сварки могут появляться колебания используемого тока, что иногда может вызывать ухудшение качества работ. Чтобы этого избежать, осцилляторы синхронизируются.

Часто для возбуждения бесконтактной дуги используются генераторы импульсного типа, в которых имеются накапливаемые резервуары, подзаряжающиеся от специального устройства. С учетом того момента, что фазное изменение сварочного тока в рабочем процессе не всегда стабильно, для организации надежной функциональности генератора требуется прибор, синхронизирующий разряд емкости в тех случаях, когда ток из дуги проходит через ноль.

На переменном токе осциллятор применяется для сварки как обычными электродами, так и элементами, применяющимися для работы с нержавейкой, цветными металлами, обработки аргоном.

Агрегаты непрерывного действия

Подобные приборы функционируют синхронно с питающим источником. Процесс возбуждение происходит посредством наложения на токоведущие части высокого напряжения и частоты. Данный ток не представляет опасности для работника, зато способен возбуждать сварочную дугу без соприкосновения электрода и обрабатываемого предмета, а за счет высокой частоты сохраняется достаточное горение дуги.

Осциллятор, виды которого имеют последовательное подключение, считаются более результативным. Ему не требуется активация в цепи источника специальной защитной системы от чрезмерного напряжения. Катушка подсоединяется последовательно к дуге. При работе разрядник издает негромкое потрескивание.

На выключенном из сети агрегате регулировочным винтом можно откорректировать искровой зазор в диапазоне от 1,5 до 2 миллиметров. Установку подобного оборудования следует доверять специалистам, поскольку непрофессиональный монтаж может угрожать здоровью и жизни работника, эксплуатирующего устройство.

Эксплуатационные условия

Осциллятор – это прибор, регистрация которого требуется в органах инспектирования электросвязи. К остальным условиям эксплуатации относятся такие требования и возможности:

• Агрегат может использоваться в закрытых помещениях и на улице.
• При дожде и снеге работать с прибором на открытом воздухе запрещено.
• Температурный режим функционирования находится в пределах от минус десяти до плюс сорока градусов.
• Эксплуатация устройства допускается при атмосферном давлении от 85 до 106 кПа и влажности не выше 98 процентов.
• Категорически не рекомендуется использовать аппарат в запыленных помещениях, особенно, где содержаться едкие газы или пары.
• Прежде, чем приступить к работе, необходимо позаботиться о надежном заземлении.

Безопасность

Чтобы понять, что такое осциллятор, для чего нужен, необходимо иметь минимальные навыки сварщика. Основные различия рассматриваемых устройств и принцип их действия приведены выше. При работе с подобными приспособлениями следует соблюдать определенные меры безопасности.

Необходимо постоянно контролировать правильность подсоединения в сварочную цепь и проверять контакты на исправность. Кроме того, следует работать с использованием защитного кожуха, который снимать и одевать нужно при выключенном от сети аппарате. Также надо периодически проверять состояние поверхности разрядника (очищать его наждачкой от нагара).

Где приобрести?

Осциллятор – это прибор, который можно купить в специализированных магазинах либо сделать своими руками. Самостоятельное его изготовление требует познания в подключении электрических схем и правильном подборе составных элементов, главным из которых является высоковольтный трансформатор.

Сделать самодельную модель можно по наиболее простой схеме. В комплект входит регулирующий напряжение (от 220 до 3 000 В) трансформатор и разрядник, выдерживающий проход мощной электрической искры.

Прибор управляется при помощи кнопки, синхронно активирующей разрядник и поступление защитного газа в район выполнения сварочных работ. Непосредственно импульсы высокой частоты, обеспечивающие эффективность процесса, вырабатываются разрядником и трансформатором, имеющим высокий вольтаж. На выходе подобное приспособление обладает положительным и отрицательным контактами. Первый подает токи от трансформатора, подсоединяется к горелке сварочного агрегата, второй – напрямую к обрабатываемым элементам.

Особенности

Для того чтобы самостоятельно изготовить данное оборудование, которое существенно облегчает сварку деталей из цветных металлов и нержавеющей стали, достаточно иметь минимальные знания электротехники и навыки сборки электрических устройств.

Главное, что нужно учитывать при сборке и использовании самодельного осциллятора, – это строгое соблюдение техники безопасности при эксплуатации электроприборов. Важно придерживаться правильности сборки электрических схем, а также применять для этого только те элементы, которые имеют оптимальные характеристики.

Вывод

Сварочный прибор осциллятор, что это такое, было рассмотрено выше. В общем можно обозначить его, как устройство, позволяющее создавать рабочую дугу, не дотрагиваясь электродом к поверхности обрабатываемых компонентов. Также оно обеспечивает дуговую стабильность.

Подобная функциональность агрегата гарантируется тем, что электроток, поступающий от сварочного оборудования, взаимодействует с аналогичной величиной высокой частоты и большим показателем напряжения. Особенно существенная помощь от рассматриваемого прибора наблюдается при работе с цветметом и нержавейкой. Большим плюсом является тот момент, что осциллятор можно собрать своими руками, не обладая при этом сверхспособностями и знаниями строения и размещения элементов электроприборов.

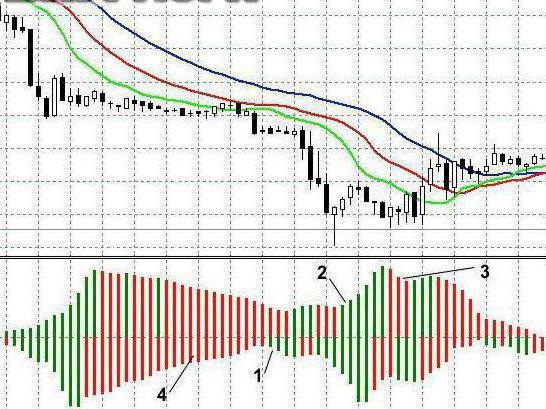
Осцилляторы для трейдера

После изучения основ технического анализа и японских свечей пытливый ум новичка всегда обращается к индикаторам. Мы уже поняли, что они показывают лишь прошлое и, зная это, можно научиться их использовать. И один из самых популярных индикаторных классов — это осцилляторы.

Прежде чем разобраться, как они работают, нужно усвоить две следующие концепции. Все индикаторы, в общей своей массе, разделяются на два следующих типа:

• опережающий индикатор;
• запаздывающий индикатор.

Разница между ними совсем не в том, что один “предсказывает” будущее, а второй нет. Сейчас мы это выясним.

Опережающие индикаторы

Как понятно из него названия, опережающий индикатор нередко указывает сигнал на вход до того, как появляется новый тренд или его разворот. И вот именно осцилляторы относятся к опережающему классу.

Два самых популярных опережающих индикатора в мире, это:

Индикаторы опережающего класса используют, в основном, при боковом движении цены, тогда, когда цена находится в консолидации и тренд отсутствует. В свою очередь, запаздывающие индикаторы лучше в тренде.

Опережающие осцилляторы нередко генерируют массу сигналов на покупку и продажу и поэтому используются в боковых коридорах. В трендовых же стратегиях чем меньше сигналов — тем лучше. Практически все опережающие индикаторы — это осцилляторы.

При этом, их «опережение» выражается в том, что осцилляторы всегда отображаются в строго ограниченном диапазоне (коридоре с фиксированным значением). Все они, так или иначе, переходят лишь из состояния перекупленности в перепроданность и наоборот. Эти уровни различаются в зависимости от типа используемого осциллятора.

Новичок сразу подумает, что опережающие лучше запаздывающих, кому же охота плестись в хвосте? Однако, это “опережение” нередко приводит к генерированию массы ложных сигналов, достаточно посмотреть, как работает тот же стохастик. Поэтому вопрос, по сути, лишь в методе их использования.

Возьмем уже описанный на сайте RSI. Он отображается строго в диапазоне от 0 до 100. При этом:

• перекупленность: RSI больше 70;
• перепроданность: RSI меньше 30.

Запаздывающие индикаторы

Эти индикаторы вовсе не хуже опережающих. Просто это принцип их работы. Они отрисовывают изменения цены медленнее но, за счет этого, лучше отображают возникновение устойчивого нового тренда.

Три самых популярных запаздывающих индикатора, это:

Эти индикаторы традиционно относятся к трендовому классу. Однако, некоторые из них можно использовать и при боковом движении. Скажем, сужение полос боллинджера означает уменьшение волатильности цены перед последующим трендом.

Это можно использовать как в БО (эксплуатировать зону низкой волатильности), так и в форексе – вход по тренду после “пробоя” это зоны:

Вот тот же канал слева, но уже более детальнее, на 1-часовом ТФ. Сразу видно, какие возможности это дает:

Использование осцилляторов

Все осцилляторы, по своей сути, используются только для двух ситуаций:

• пересечение;
• дивергенция.

Пересечение — это когда осциллятор пересекает определенный уровень. Например, когда RSI уверенно снижается за уровень 70, следовательно, цена выходит из состояния перекупленности, а общий уровень цены идет на снижение.

О дивергенции мы поговорим отдельно в следующем уроке. Это важная тема, ибо именно ради дивергенции осцилляторы и применяются. Это расхождение движения цены и показаний осциллятора. Например:

Перекупленность и перепроданность

В описании множества осцилляторов, таких как RSI, вам встретятся такие понятия, как “перекупленность” и “перепроданность”. Скажем, вот так это выглядит на графике:

Либо:

Что означают эти термины? Это вовсе не обозначение того, что какой-то актив купили больше или меньше, и уж тем более не данные по объемам торгов.

Этими терминами просто указывается на нетипичное движение цены. Смотрите на это так: цена всегда, так или иначе, тяготеет к усредненному значению, то есть к тренду. Чем активнее и быстрее цена от этой средней линии отклоняется (в этом качестве часто используется SMA 20) — тем больше оснований считать, что на рынке происходит всплеск, так сказать, нездоровой заинтересованности быков и медведей.

Вот именно это и означают эти термины.

• Перекупленность — актив быстро и решительно покупали, активные быки.
• Перепроданность — медведи у руля.

Любые отклонения от «средней температуры» можно использовать в свою пользу и именно их показывают осцилляторы. Небольшой анализ истории сразу вам покажет, где и как перепроданность и перекупленность используются.

При этом не забывайте, что сам факт нахождения линии осциллятора в этих зонах вовсе не четкий, однозначный сигнал (это было бы слишком просто). А лишь намек вам, как трейдеру, обратить на цену в этой зоне особое внимание.

Затем, используя инструменты технического анализа и безиндикаторные системы вы сможете использовать такие ситуации в свою пользу.

Осцилляторные стратегии

У каждого осциллятора есть свое описание. Подобрать себе подходящий вариант вы сможете в каталоге осцилляторов. А мы рассмотрим несколько примеров осцилляторных стратегий.

Осциллятор, как и любой индикатор, должен дополнять технический анализ: теорию Доу, тренды, каналы, поддержку и сопротивление. Это — обязательно. Как и любой индикатор, его нельзя использовать слепо для входа в рынок.

Нередко для работы применяется сразу несколько осцилляторов, показания которых должны совпадать. Так создаются осцилляторные стратегии, парочку примеров которых мы рассмотрим далее.

Пересечение скользящих + MACD

Инструменты:

Пример использования:

Stochactic RSI + Awesome Oscillator

Немного наблюдательности и вы сами сможете сочетать эти осцилляторы в различных комбинациях. Но я бы не советовал этим особенно увлекаться и лепить их по 20 штук на график.

Чтобы добиться в трейдинге успеха, вы должны развивать в себе комплексное понимание рынка, для начала усвоив простые, базовые основы технического анализа – теорию Доу, тренды, поддержку/сопротивление и т.д. Лишь потом, шаг за шагом, вы будете добавлять в свою систему различные инструменты, в том числе и осцилляторы (если они понадобятся).

Ну и в публичной библиотеке TradingView вы найдете сотни осцилляторов на любой вкус и цвет. Скажем, Rahul Mohinder Oscillator помогает выловить рыночные фазы:

Рыночные осцилляторы

В то время как обычные осцилляторы предназначены для работы с любыми активами, существует целый класс рыночных осцилляторов, что обычно используются для анализа индексов, таких как S&P 500, а не отдельно взятых активов. Таким образом анализируется как настроение участников рынка, так и его текущая волатильность.

Впрочем, никто не мешает многие из них использовать и с валютными парами. Просто помните, что в основе их создания лежит стремление анализировать именно рыночные сегменты.

Индексы волатильности

Индексы, что показывают волатильность определенного рынка. При этом, кстати, многие такие индексы и сами торгуются на биржах.

Один из самых известных — это индекс волатильности биржи CBOE, он же CBOE Volatility Index (VIX). Отображает ожидания рынка в масштабе 30 дней и состоит из волатильности целого ряда индексных опционов кол и пут для индекса S&P 500. При этом чем больше значение этого индекса, тем больше рыночные риски.

Как правило, индексы волатильности и сами индексы негативно коррелируют друг с другом (идут в разных направлениях). Если все хорошо и цены на рынке растут, уровень риска падает, поэтому индекс волатильности снижается. Когда же рынок падает то, соответственно, растут и риски (как и индекс волатильности).

При этом:

• VIX – волатильность S&P 500;
• VXN – волатильность Nasdaq 100;
• VXD – волатильность DJIA.

Однако, далеко не все работают с этими индексами, в бинарных и форексе это достаточно редкий гость. Поэтому для прогнозирования других активов, скажем, валютных пар используются синтетические VIX-осцилляторы. Один из самых известных  – индикатор Vix Fix от Ларри Вильямса. Он же, кстати, самый популярный индикатор в Tradingview.

Advance Decline Line

Еще один популярный рыночный осциллятор — ADL, он же Advance Decline Line. Используется профессиональными трейдерами вот уже несколько десятилетий. Суть индикатора — сравнение общего направления движения цены. В применении к валютам, индикатор сравнивает число свечей вверх с их количеством, что шло вниз. Затем из первого числа вычитается (прибавляется) второе и формируется общее значение.

Скажем, если вчера общее значение было, условно, 100 и цена на 5 свечей вверх шла больше, нежели вниз, к значению 100 добавляется 5 и получается ADL = 105. По факту, с помощью ADL определяют рыночные тренды и дивергенции. Основной сигнал — когда движение ADL не совпадает с движением цены и, тем самым, предвосхищает смену рыночного тренда.

Осциллятор McClellan

Индикатор моментума, также основанный на принципе сравнения числа бычьих и медвежьих свечей. Основан на вычитании средней скользящей со значением 39 индикатора Net Advances от скользящей со значением 19. Принцип схож с использованием MACD. Зеленая зона — цена демонстрирует тенденцию к росту, красная — к падению. Здесь также весьма ценна дивергенция.

Разновидность этого осциллятора — индекс суммирования McClellan Summation Index, основанный на округлении значений McClellan Oscillator и используемый для определения долговременной силы рынка.

Когда значение McClellan Summation Index больше 1000 — это указание на то, что тренд достиг своего потолка. И напротив, значение минус 1000 указывает на потенциальное дно рынка.

50 осцилляторов

В платформе TradingView представлено множество осцилляторов, как сделанных с нуля, так и модификаций известных систем. Достаточно ввести в поле Search одно из названий ниже и вы сразу получите осциллятор на своем графике:

1. Advance Decline Line
2. Price Oscillator
3. Volume Oscillator
4. Awesome Oscillator
5. Chaikin Oscillator
6. Klinger Oscillator
7. Klinger Volume Oscillator (KVO)
8. Ultimate Oscillator
9. SMI Ergodic Oscillator
10. Chande Momentum Oscillator
11. Detrended Price Oscillator
12. Directional Movement Index Oscillator
13. OBV Oscillator
14. Derivative Oscillator
15. Rahul Mohindar Oscillator (RMO)
16. Awesome Oscillator (Bill Williams)
17. Premier Stochastic Oscillator
18. Vervoort Smoothed Oscillator
19. ElliotWave Oscillator
20. Blau’s Ergodic Chandlestick Oscillator
21. Forecast Oscillator
22. KaseCD и Kase Peak Oscillator
23. Rainbow Charts Oscillator
24. rs_Chande’s Momentum Oscillator
25. Pivot Detector Oscillator
26. CCT Bollinger Bands Oscillator
27. Constance Brown Derivative
28. Pretty Good Oscillator
29. Projection Oscillator
30. Hurst Oscillator
31. Guppy Oscillator
32. Linda Raschke Oscillator
33. Ian Oscillator
34. ASI Oscillator
35. WaveTrend Oscillator
36. Kase Peak Oscillator
37. DT Oscillator
38. Vervoort Heiken-Ashi Candlestick Oscillator
39. Ehler’s Universal Oscillator
40. Cycle Channel Oscillator
41. Firefly Oscillator
42. Absolute Strength Index Oscillator
43. DiNapoli Detrended Oscillator
44. Pivot Detector Oscillator, by Giorgos E. Siligardos
45. TFS: Volume Oscillator
46. Dynamic Momentum Oscillator (Dynamo)
47. CMO Oscillator with Filter
48. CMO & WMA Oscillator
49. CMOabs Oscillator
50. UCS_Murrey’s Math Oscillator_V2
51. TheLark: Directional Movement Index Oscillator
52. PE_Price_Oscillator
53. LBR Oscillator
54. Snake Oscillator 1.1
55. Accel Oscillator
56. [RS]Impulse Oscillator V0
57. [RS]Power Correlation Oscillator (GOLD) V0
58. [RS]Power Correlation Oscillator (DOLLAR) V0

Правильная отработка осциллятора

Мой любимый осциллятор, дополняющий безиндикаторную торговлю – это, безусловно, Stochastic, что иногда помогает при боковом движении цены.

Однако, чтобы научиться его использовать у меня ушло более года. Каждый день я искал на истории цены ситуации, где стохастик работал, а где нет. Я сделал множество скриншотов (более 2000 на данный момент) его поведения в различных ситуациях. Отрабатывал его постоянно, сочетал с различными элементами как технического анализа и безиндикаторной торговли. Лишь спустя это время у меня начало получаться — стало понятно, где осциллятор работает лучше всего, а где вообще бесполезен и на график его можно не добавлять.

Запомните: любой инструмент нужно отрабатывать до совершенства. У новичков же история совсем другая. Они ставят осциллятор, он чаще ошибается, нежели дает точные прогнозы (естественно). Так и должно быть, иначе трейдингом мог бы заниматься любой первоклассник.

Лишь после наработки достаточного объема опыта вы сможете воспользоваться осциллятором как надежным помощником и не ранее. Не надо лениться — отрабатывайте инструмент, пока он не запищит и не станет вашим любимым, только так.

Осцилляторы на валютном рынке. Сигналы осциллятора

Что такое осцилляторы на Форекс?

В техническом анализе форекс осцилляторы являются индикаторами скорости движения цены за конкретный промежуток времени. Они относятся к опережающему индикатору, который может передвигаться вокруг нулевой линии в промежутке от 0 до 100%. В те отрезки времени, когда цена стабильна, она либо движется только в пределах канала, либо ненадолго приостанавливается для того, чтобы развернуться. Осциллятор же на рынке Форекс как раз предназначен для того, чтобы найти точки, после которых цена будет двигаться либо по тренду, либо к обратной границе канала.

Главными понятиями, которые нужны при использовании осцилляторов, являются понятия перепроданности и перекупленности. Так называются ситуации, при которых значение индикатора доходит до верхней или нижней границы шкалы:

• Понятие перекупленности используется, когда говорится о том, что цена находится в пределах верхней границы, а вероятность её повышения крайне мала.
• Понятие перепроданности, наоборот, используется в ситуациях, когда цена находится около нижней границы, а ее дальнейшее падение маловероятно.

Какие сигналы дают форекс осцилляторы?

• Выявление уровней перекупленности и перепроданности

Один из основных способов использования осцилляторов на рынке Форекс – это поиск отрезков перекупленности и перепроданности. Этим значениям, как правило, соответствуют отметки 20 и 80 при сильном трендовом движении, в момент его затишья, и 25 и 75 – при боковом тренде во время движения в границах канала. Сигнал на продажу берется, если осциллятор поднялся выше значения перекупленности, а потом пересек его назад. Обязательно дождаться обратного пересечения. Сигнал на покупку – если осциллятор опустился ниже порога перепроданности, а затем пересек его вверх.

• Определение дивергенций

Второй эффективный способ использования осцилляторов – поиск дивергенции и конвергенции (расхождения) между ценой на графике и осциллятором на рынке Форекс: цена показывает новый максимум (при восходящем тренде, в нисходящем тренде все будет наоборот), а осциллятор образует вершину ниже предыдущей.

Поскольку осцилляторы дают ложные сигналы в тренде, сигнал дивергенции можно учитывать, только если рынок находится в коррекционной волне, а не в импульсной. Искать вход по осциллятору против тренда в надежде, что тренд изменится, — это заведомо убыточная стратегия, зарабатывать на которой могут единицы.

• Пересечение осциллятором нулевого уровня

Если индикатор пересекает нулевой уровень снизу вверх, это может служить дополнительным сигналом к покупке. Если наоборот – к продаже.

• Анализ взаимодействия линий на осцилляторе

Еще один вероятный сигнал – ситуация, когда более быстрая линия на осцилляторе пересекает более медленную. Соответственно, если такое пересечение происходит в направлении снизу вверх – имеем сигнал на покупку, и наоборот. Если такие пересечения в одном направлении происходят несколько раз подряд, а также обе линии продолжают дальнейшее параллельное движение по направлению к нулевому уровню, — это говорит об усилении сигнала. Такие движения линий хорошо наблюдать, к примеру, на стохастическом осцилляторе.

• Поиск фигур технического анализа

Некоторые трейдеры используют осцилляторы для поиска фигур технического анализа, например, Голова и плечи, Алмаз, Клин. Обычно эти фигуры работают на ценовом графике, но в некоторых случаях осцилляторы тоже рисуют ту или иную фигуру.

Какие осцилляторы считаются самыми популярными?

Осцилляторы являются популярными индикаторами в среде трейдеров, в том числе и на валютном рынке. Основной их привлекательностью является простота идентификации сигналов на открытие сделки, которые дают данные ценовые фильтры.

Существует большое количество различных осцилляторов, в том числе:

Полезные статьи по теме

Что такое осциллятор? Принцип работы, виды, применение

Осциллятор – это схема, которая производит непрерывную, повторяющуюся, переменную форму волны без какой-либо подачи на входе. Осцилляторы в основном преобразовывают однонаправленный ток из источника постоянного тока в переменную форму волны, которая имеет желательную частоту. Это достижимо благодаря компонентам схемы.

Принцип работы.

Базовый принцип работы осцилляторов может быть объяснён анализом поведения колебательного LC-контура схемы, показанной на рисунке 1, которая задействует индуктор L и предварительно полностью заряженный конденсатор C. Конденсатор начинает разряжаться через индуктор, что является следствием превращения его электрической энергии в электромагнитное поле. Это поле может быть аккумулировано индуктором.

Однажды конденсатор разряжается полностью, и в схеме нет электрического тока. Как бы там ни было, после этого аккумулированное электромагнитное поле генерирует противоэлектродвижущую силу, что происходит из-за движения тока через схему в том же направлении, что и ранее.

Этот поток тока через схему продолжается вплоть до того момента, пока не разрушится электромагнитное поле, что является результатом обратного преобразования электромагнитной энергии в электрическую форму, вынуждая цикл повторяться. Как бы там ни было, теперь конденсатор заряжается с отрицательной полярностью, благодаря чему и получается осциллирующая форма волны на выходе.

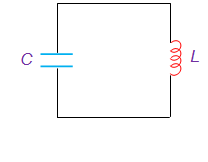
Рисунок 1 Схема колебательного LC-контура

 

Как бы там ни было, колебания, которые появляются из-за взаимопревращения двух форм энергии, не могут длиться вечно, ведь они подвержены эффекту потери энергии из-за сопротивления схемы. В результате амплитуда этих колебаний постоянно уменьшается, стремясь к нулю. Колебания просто исчезают естественным образом.

 

Это показывает, что нужно получить колебания, которые продолжаются во времени и имеют постоянную амплитуду, которая нужна для компенсации потери энергии. Тем не менее, важно отметить, что поступающая энергия должна точно контролироваться, и она должна быть равна потерянной энергии для получения колебаний с постоянной амплитудой.

 

Если энергии будет поступать больше, чем теряться, то амплитуда колебаний будет возрастать (Рисунок 2a), что приведёт к искаженному выходу. Если энергии, которая поступает, будет меньше, чем той, которая теряется, то амплитуда колебаний будет уменьшаться (Рисунок 2b), приводя к недостаточным колебаниям.

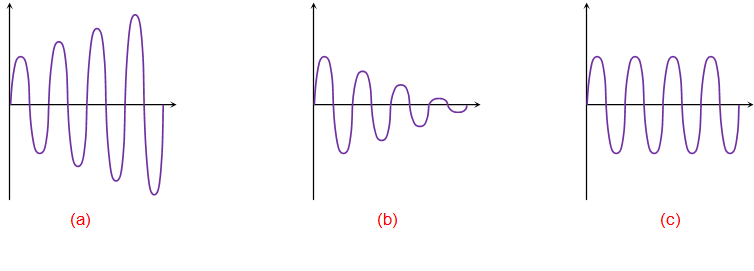
Рисунок 2 (a) Возрастающие Колебания (b) Затухающие Колебания (с) Колебания с Постоянной Амплитудой

 

Фактически, осцилляторы являются ни чем иным как усилителями схемы, которые производятся с позитивной или восстанавливающей обратной связью, где часть сигнала на выходе является обратной связью со входом (Рисунок 3). Здесь усилитель содержит активный усиливающий элемент, который может быть транзистором или операционным усилителем, и синфазный сигнал обратной связи является ответственным за поддержку колебаний за счёт завершения потерь в схеме.

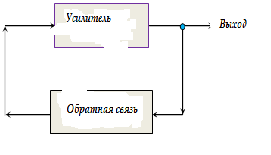
Рисунок 3 Типичный осциллятор

 

Когда блок питания включен, осцилляторы начинают работу из-за наличия электронного шума. Эти шумовые сигналы повторяются по циклу, усиливаются и сходятся в одночастотную синусоидальную волну очень быстро. Выражение коэффициента усиления закрытого цикла осциллятора, показанного на рисунке 3, выглядит как:

 

 

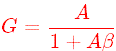
Здесь A является коэффициентом усиления напряжения усилителя и ß является коэффициентом усиления схемы обратной связи. Если Aß > 1, то колебания будут усиливаться в амплитуде (Рисунок 2a). Если же Aß < 1, то колебания будут затухать (Рисунок 2b). Если Aß = 1, то колебания будут иметь постоянную амплитуду (Рисунок 2c).

 

Другими словами, это указывает на то, что если коэффициент усиления цикла обратной связи мал, то колебания затухают, в то время как при большом коэффициенте результат на выходе искажается. И только если данный коэффициент равен единице, у колебаний будет постоянная амплитуда, порождающая самостоятельный цикл колебаний.

 

Осцилляторы делятся на две категории, а именно на линейные или синусоидальные осцилляторы и разряжающие осцилляторы. В синусоидальных осцилляторах поток энергии всегда идёт от активных элементов схемы к пассивным, и частота колебаний определяется за счёт обратной связи.

 

Как бы там ни было, в случае с разряжающими осцилляторами, происходит обмен энергии между активными и пассивными компонентами, и частота колебаний определяется за счёт зарядки и разрядки стационарных элементов, вовлечённых в процесс. Синусоидальные осцилляторы производят слабо изменяющиеся синусоидальные волны на выходе. Разряжающие осцилляторы создают несинусоидальные формы волн (пилообразные, треугольные или квадратные).

 

Осцилляторы могут быть классифицированы на различные типы, в зависимости от того, какой параметр рассматривается, а именно:

1. Классификация, основанная на механизме обратной связи: осцилляторы с положительной обратной связью и осцилляторы с отрицательной обратной связью.

2. Классификация, основанная на форме волны на выходе: осцилляторы с синусоидальной волной, осцилляторы с квадратной или треугольной формой волны, осцилляторы с волной большого размаха (они создают пилообразную форму волны на выходе), и т.д.

3. Классификация, основанная на частоте сигнала на выходе: осцилляторы с низкой частотой, аудио осцилляторы (они имеют частоту на выходе, входящую в диапазон аудио), осцилляторы с частотой радио, осцилляторы с высокой частотой, осцилляторы с очень высокой частотой, осцилляторы с ультра высокой частотой. и т.д.

4. Классификация, основанная на типе используемого контроля частоты: RC осцилляторы, LC осцилляторы, кристаллические осцилляторы (которые используют кристаллы кварца для стабильной частоты волны на выходе), и т.д.

5. Классификация, основанная на природе частоты колебаний волн на выходе: осцилляторы с постоянной частотой и осцилляторы с переменной или перестраиваемой частотой.

В качестве примеров осцилляторов можно привести осцилляторы Армстронга, осцилляторы Хартли, осцилляторы Колпиттса, осцилляторы Клэппа, попарносдвоенные осцилляторы, динатронные осцилляторы, осцилляторы Мейснера, опто-электронные осцилляторы, пересекающие осцилляторы, осцилляторы с фазовым сдвигом, осцилляторы Робинсона, триод-тетроидные осцилляторы, мостовые осцилляторы, осцилляторы Пирсона-Ансона, кольцевые осцилляторы, осцилляторы с линией задержки, осцилляторы Ройера, электронные сдвоенные осцилляторы и многоволновые осцилляторы.

 

Осцилляторы портативны и недороги, благодаря чему они широко применяются в кварцевых часах, радиоприемниках, компьютерах, металло-детекторах, оглушающем оружии, инверторах, ультразвуковых и радиочастотных приспособлениях.

 

Пишите комментарии, дополнения к статье, может я что-то пропустил. Загляните на карту сайта, буду рад если вы найдете на моем сайте еще что-нибудь полезное.

Поделиться ссылкой:

Значение слова ОСЦИЛЛЯТОР. Что такое ОСЦИЛЛЯТОР?

Осцилля́тор (лат. oscillo — качаюсь) — система, совершающая колебания, то есть показатели которой периодически повторяются во времени.

Физика

Понятие осциллятора играет важную роль в физике и повсеместно используется, например, в квантовой механике и квантовой теории поля, теории твёрдого тела, электромагнитных излучений, колебательных спектров молекул. В принципе это понятие используется по крайней мере при описании почти любой линейной или близкой к линейности физической системы, и уже поэтому пронизывает практически всю физику. Примеры простейших осцилляторов — маятник и колебательный контур.

Гармонический осциллятор;

Осциллятор Дуффинга;

Осциллятор Чуа;

Осциллятор Ван дер Поля;

Ослабленный осциллятор;

LC-осциллятор.

Электроника и радиотехника

Генератор сигналов

Кварцевый генератор;

Генератор Армстронга;

Генератор Вачкара;

Генератор Клаппа;

Генератор Колпитца;

Генератор Хартли;

Кольцевой генератор.

Экономика

Осцилляторы — (в техническом анализе) — это класс индикаторов технического анализа, которые характеризуют состояние перекупленности (overbought) или перепроданности (oversold) рынка. Они, как правило, эффективны при стационарном состоянии рынка, когда цена двигается в пределах сравнительно узкого «рыночного коридора». Например, Осциллятор Макклеллана.

Физилология

Клетка-осциллятор

Компьютерное моделирование

Осциллятор — класс конфигураций в «Жизни» — созданной Конвеем модели клеточного автомата.

Техника, технология

Осциллятор в сварке — устройство, предназначенное для бесконтактного возбуждения электрической дуги и стабилизации горения дуги при сварке малыми токами.

Бурение нефтяных наклонно-горизонтальных скважин

Скважинный осциллятор — устройство для механического способа снижения сил трения бурильной колонны о стенки скважины.

Гармонический осциллятор — Википедия

У этого термина существуют и другие значения, см. Осциллятор.

Гармони́ческий осцилля́тор (в классической механике) — система, которая при выведении её из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x:

F=−kx{\displaystyle F=-kx},

где k — постоянный коэффициент.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

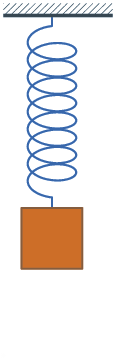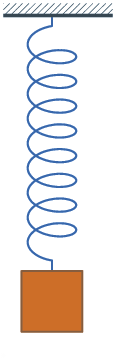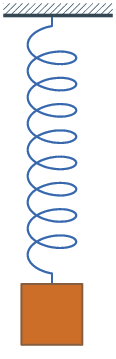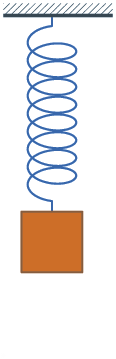
Свободные колебания системы груз—пружина без затухания.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди немеханических аналогов гармонического осциллятора можно выделить электрический гармонический осциллятор (см. LC-цепь).

Свободные колебания консервативного гармонического осциллятора[править | править код]

Уравнение и его решения[править | править код]

Пусть x — смещение материальной точки относительно её положения равновесия, а F — действующая на точку возвращающая сила любой природы вида

F=−kx{\displaystyle F=-kx},

где k = const. Тогда, используя второй закон Ньютона, можно записать ускорение как

a=−kmx{\displaystyle a=-{\frac {k}{m}}x}.

Обозначая ω02=k/m{\displaystyle {\omega _{0}}^{2}=k/m} и заменяя a на вторую производную от координаты по времени x¨{\displaystyle {\ddot {x}}}, имеем

x¨+ω02x=0{\displaystyle {\ddot {x}}+\omega _{0}^{2}x=0}.

Это дифференциальное уравнение описывает поведение консервативного гармонического осциллятора. Величину ω0{\displaystyle \omega _{0}} называют циклической частотой. (Имеется в виду круговая частота, измеряющаяся в радианах за секунду. Чтобы перевести её в частоту, выражающуюся в герцах, надо разделить на 2π{\displaystyle 2\pi }.)

Будем искать решение этого уравнения в виде^[1]

x(t)=Asin⁡(ωt+φ){\displaystyle x(t)=A\sin \left(\omega t+\varphi \right)}.

Здесь A — амплитуда, ω — частота колебаний, φ — начальная фаза.

Подставляем в дифференциальное уравнение и получаем:

x¨(t)=−Aω2sin⁡(ωt+φ){\displaystyle {\ddot {x}}(t)=-A\omega ^{2}\sin(\omega t+\varphi )},

−Aω2sin⁡(ωt+φ)+ω02Asin⁡(ωt+φ)=0{\displaystyle -A\omega ^{2}\sin(\omega t+\varphi )+\omega _{0}^{2}A\sin(\omega t+\varphi )=0}.

Амплитуда сокращается. Значит, она может иметь любое значение (в том числе и нулевое — это означает, что материальная точка покоится в положении равновесия). На синус также можно сократить, так как равенство должно выполняться в любой момент времени t. Таким образом, остаётся условие для частоты колебаний:

−ω2+ω02=0,{\displaystyle -\omega ^{2}+\omega _{0}^{2}=0,}

ω=±ω0.{\displaystyle \omega =\pm \omega _{0}.}

Отрицательную частоту можно отбросить, так как произвол в выборе здесь знака покрывается произволом выбора начальной фазы.

Общее решение уравнения записывается в виде:

x(t)=Asin⁡(ω0t+φ),{\displaystyle x(t)=A\sin \left(\omega _{0}t+\varphi \right),}

где A и φ — произвольные постоянные. Эта запись исчерпывает все решения дифференциального уравнения, так как позволяет удовлетворить любым начальным условиям.

Итого, консервативный гармонический осциллятор может совершать чисто гармонические колебания с частотой, равной его собственной частоте, с амплитудой любой величины и с произвольной начальной фазой.

Простое гармоническое движение[править | править код]

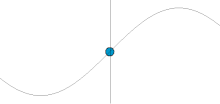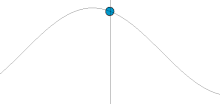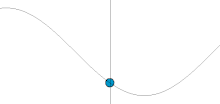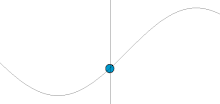Простое гармоническое движение. На этой анимированной картинке по вертикальной оси отложена координата частицы (x в формуле), а по горизонтальной оси отложено время (t).

Движение, совершаемое консервативным гармоническим осциллятором, носит название простого гармонического движения. Это движение не является ни вынужденным, ни затухающим.

Оно периодическое: тело колеблется с частотой ω₀ около положения равновесия по синусоидальному закону. Каждое последующее колебание такое же, как и предыдущее; период, частота и амплитуда колебаний остаются постоянными.

Учитывая, что ω₀ = 2πf, получим

f=12πkm,{\displaystyle f={\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}},}

и, поскольку T = 1/f, где T — период колебаний,

T=2πmk.{\displaystyle T=2\pi {\sqrt {\frac {m}{k}}}.}

Эти формулы показывают, что период и частота не зависят от амплитуды и начальной фазы движения.

Частота движения определяется характерными свойствами системы (например, массой движущегося тела), в то время как амплитуда и начальная фаза определяются начальными условиями — координатой и скоростью тела в момент начала колебаний. Кинетическая и потенциальная энергии системы также зависят от этих свойств и условий.

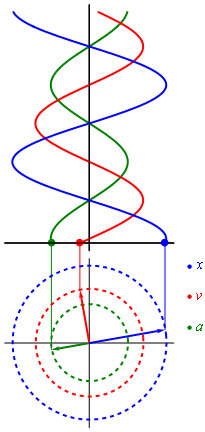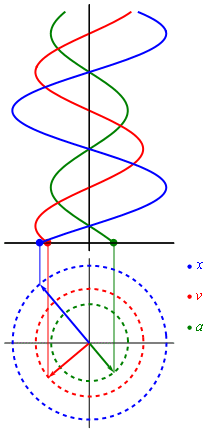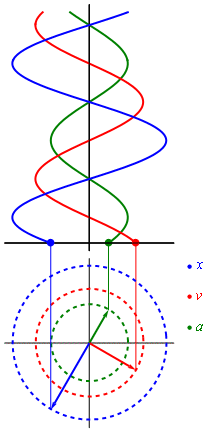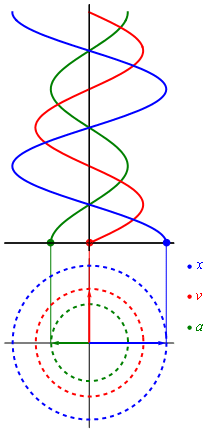Положение, скорость и ускорение простого гармонического движения на фазовой плоскости

Используя приёмы дифференциального исчисления, можно получить скорость и ускорение материальной точки как функции времени:

v(t)=dxdt=Aω0cos⁡(ω0t+φ){\displaystyle v(t)={\frac {\mathrm {d} x}{\mathrm {d} t}}=A\omega _{0}\cos(\omega _{0}t+\varphi )},

a(t)=d2xdt2=−Aω02sin⁡(ω0t+φ){\displaystyle a(t)={\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-A\omega _{0}^{2}\sin(\omega _{0}t+\varphi )}.

Кинетическая энергия записывается в виде

T=12mv2(t)=12kA2cos2⁡(ω0t+φ){\displaystyle T={\frac {1}{2}}mv^{2}(t)={\frac {1}{2}}kA^{2}\cos ^{2}(\omega _{0}t+\varphi )},

а потенциальная энергия составляет

U=12kx2(t)=12kA2sin2⁡(ω0t+φ){\displaystyle U={\frac {1}{2}}kx^{2}(t)={\frac {1}{2}}kA^{2}\sin ^{2}(\omega _{0}t+\varphi )}.

Тогда получается, что полная энергия

E=12kA2{\displaystyle E={\frac {1}{2}}kA^{2}}

имеет постоянное значение. Это отражает «консервативность» осциллятора, то есть отсутствие энергетических потерь.

Простое гармоническое движение можно рассматривать как математическую модель различных видов движения, таких, например, как колебание пружины. Другими случаями, которые могут приближённо рассматриваться как простое гармоническое движение, являются движение маятника и вибрации молекул.

Простое гармоническое движение является основой некоторых способов анализа более сложных видов движения. Одним из таких способов является способ, основанный на преобразовании Фурье, суть которого сводится к разложению более сложного вида движения в ряд простых гармонических движений.

Примеры осцилляторов[править | править код]

Любая система, в которой происходит простое гармоническое движение, обладает двумя ключевыми свойствами:

• когда система выведена из состояния равновесия, должна существовать возвращающая сила, стремящаяся вернуть систему в равновесие;
• возвращающая сила должна в точности или приближённо быть пропорциональна перемещению.

Ниже представлено несколько примеров.

Горизонтальная система груз—пружина

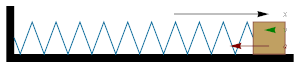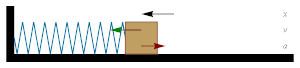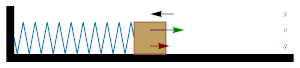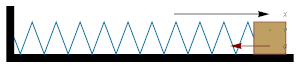Положение, скорость и ускорение гармонического осциллятора

Типичным примером системы, в которой происходит простое гармоническое движение, является идеализированная система груз—пружина, в которой груз присоединён к пружине и находится на горизонтальной поверхности. Если пружина не сжата и не растянута, то на груз не действует никаких переменных сил и он находится в состоянии механического равновесия. Однако, если груз вывести из положения равновесия, пружина деформируется и с её стороны будет действовать сила, стремящаяся вернуть груз в положение равновесия. В случае системы груз—пружина такой силой является сила упругости пружины, которая подчиняется закону Гука:

F=−kx{\displaystyle F=-kx},

где k имеет вполне конкретный смысл — это коэффициент жёсткости пружины.

Однажды смещённый груз подвергается действию возвращающей силы, ускоряющей его и стремящейся вернуть в начальную точку, то есть в положение равновесия. По мере того, как груз приближается к положению равновесия, возвращающая сила уменьшается и стремится к нулю. Однако в положении x = 0 груз обладает некоторым количеством движения (импульсом), приобретённым благодаря действию возвращающей силы. Поэтому груз проскакивает положение равновесия, начиная снова деформировать пружину (но уже в противоположном направлении). Возвращающая сила будет стремиться замедлить его, пока скорость не станет равной нулю; и сила вновь будет стремиться вернуть груз в положение равновесия.

Если нет потерь энергии, груз будет колебаться как описано выше; такое движение является периодическим.

Вертикальная система груз—пружина

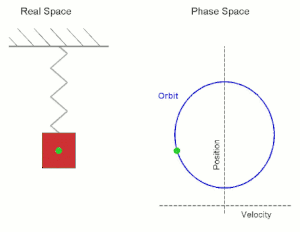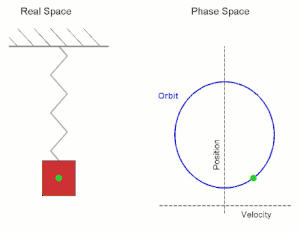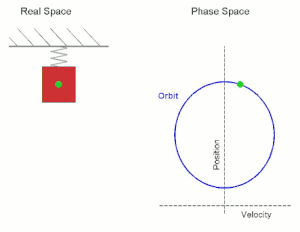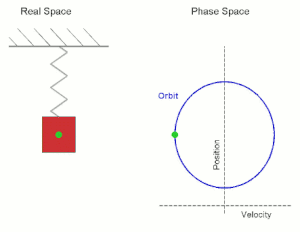Простое гармоническое движение, показанное одновременно в реальном пространстве и в фазовом пространстве. Real Space — реальное пространство; Phase Space — фазовое пространство; velocity — скорость; position — положение (позиция).

В случае вертикально подвешенного на пружине груза, наряду с силой упругости, действует сила тяжести, то есть суммарно сила составит

F=−kx−mg{\displaystyle F=-kx-mg}.

Если сделать замену переменной, чтобы оперировать не величиной x{\displaystyle x}, а величиной X=x+mg/k{\displaystyle X=x+mg/k}, то уравнение движения примет вид, идентичный случаю горизонтальной геометрии, только для переменной X{\displaystyle X}.

Колебания будут происходить с той же частотой ω0=k/m{\displaystyle \omega _{0}={\sqrt {k/m}}}. Однако, если в горизонтальном случае равновесию отвечало состояние недеформированной пружины, то в вертикальном варианте пружина в равновесии будет растянута. Зависимости частоты от величины ускорения свободного падения g{\displaystyle g} при этом нет; g{\displaystyle g} влияет лишь на сдвиг положения равновесия mg/k{\displaystyle mg/k}.

Измерения частоты (или периода) колебаний груза на пружине используются в устройствах для определения массы тела — так называемых массметрах, применяемых на космических станциях, когда весы не могут функционировать из-за невесомости.

Универсальное движение по окружности

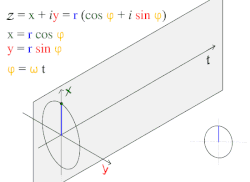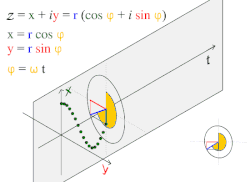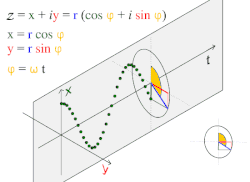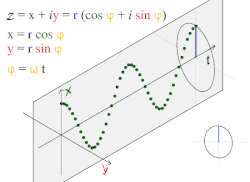Движение по кругу и гармоническое движение

Простое гармоническое движение в некоторых случаях можно рассматривать как одномерную проекцию универсального движения по окружности.

Если объект движется с постоянной угловой скоростью ω по окружности радиуса r, центром которой является начало координат плоскости x − y, то такое движение вдоль каждой из координатных осей является простым гармоническим с амплитудой r и круговой частотой ω.

Груз как простой маятник

Простое гармоническое движение маятника без затухания.

В приближении малых углов движение простого маятника является близким к простому гармоническому. Период колебаний такого маятника, прикреплённого к стержню длиной ℓ, даётся формулой

T=2πℓg.{\displaystyle T=2\pi {\sqrt {\frac {\ell }{g}}}.}

где g — ускорение свободного падения. Это показывает, что период колебаний не зависит от амплитуды и массы маятника, но зависит от g, поэтому, при той же самой длине маятника, на Луне он будет качаться медленнее, так как там слабее гравитация и меньше значение ускорения свободного падения.

Указанное приближение является корректным только при небольших углах отклонения, поскольку выражение для углового ускорения пропорционально синусу координаты:

ℓmgsin⁡θ=Iα,{\displaystyle \ell mg\sin \theta =I\alpha ,}

где I — момент инерции; в данном случае I = m ℓ ². Небольшие углы реализуются в условиях, когда амплитуда колебаний значительно меньше длины стержня.

Когда угол θ мал, можно считать, что sin θ ≈ θ, и выражение принимает вид:

ℓmgθ=Iα,{\displaystyle \ell mg\theta =I\alpha ,}

что делает угловое ускорение прямо пропорциональным углу θ, а это удовлетворяет определению простого гармонического движения.

Свободные колебания гармонического осциллятора с затуханием[править | править код]

Уравнение и его решения[править | править код]

При рассмотрении осциллятора с затуханием за основу берётся модель консервативного осциллятора, в которую добавляется сила вязкого трения. Сила вязкого трения направлена против скорости движения груза относительно среды и прямо пропорциональна этой скорости. Тогда полная сила, действующая на груз, записывается так:

F=−kx−αv.{\displaystyle F=-kx-\alpha v.}

Используя второй закон Ньютона, получаем дифференциальное уравнение, описывающее затухающий осциллятор:

x¨+2γx˙+ω02x=0.{\displaystyle {\ddot {x}}+2\gamma {\dot {x}}+\omega _{0}^{2}x=0.}

Здесь введены обозначения:

• 2γ=α/m{\displaystyle 2\gamma =\alpha /m}. Коэффициент γ{\displaystyle \gamma } носит название постоянной затухания. Он имеет размерность частоты.
• ω0=km{\displaystyle \omega _{0}={\sqrt {k \over m}}}. Величину ω0{\displaystyle \omega _{0}} называют собственной частотой системы. Она тоже имеет размерность частоты.

Решение распадается на три случая.

• При малом трении (γ<ω0{\displaystyle \gamma <\omega _{0}}) общее решение записывается в виде:

x(t)=Ae−γtsin(ωft+φ),{\displaystyle x(t)=Ae^{-\gamma t}sin(\omega _{f}t+\varphi ),}

где ωf=ω02−γ2{\displaystyle \omega _{f}={\sqrt {\omega _{0}^{2}-\gamma ^{2}}}} — частота свободных колебаний.

• Затухание γ=ω0{\displaystyle \gamma =\omega _{0}} называют критическим. Начиная с такого значения показателя затухания, осциллятор будет совершать так называемое неколебательное движение. В граничном случае движение происходит по закону:

 x(t)=(A+Bt)e−γt.{\displaystyle \ x(t)=(A+Bt)e^{-\gamma t}.}

• При сильном же трении γ>ω0{\displaystyle \gamma >\omega _{0}} решение выглядит следующим образом:

x(t)=Ae−β1t+Be−β2t,{\displaystyle x(t)=Ae^{-\beta _{1}t}+Be^{-\beta _{2}t},}

где β1,2=γ±γ2−ω02.{\displaystyle \beta _{1,2}=\gamma \pm {\sqrt {\gamma ^{2}-\omega _{0}^{2}}}.}

Движение при наличии затухания[править | править код]

Характер движения затухающего осциллятора зависит от постоянной затухания γ{\displaystyle \gamma }. Помимо указанной постоянной, затухание осциллятора также часто характеризуют безразмерным параметром, называемым добротностью. Добротность обычно обозначают буквой Q{\displaystyle Q}. По определению, добротность равна:

Q=ω02γ.{\displaystyle Q={\frac {\omega _{0}}{2\gamma }}.}

Чем больше добротность, тем медленнее затухают колебания осциллятора.

Критическое затухание γ=ω0{\displaystyle \gamma =\omega _{0}} примечательно тем, что именно при таком затухании осциллятор быстрее всего оказывается в положении равновесия. Если трение меньше критического, он дойдёт до положения равновесия быстрее, однако «проскочит» его по инерции и будет совершать колебания. Если трение больше критического, то осциллятор будет экспоненциально стремиться к положению равновесия, но тем медленнее, чем больше трение.

Поэтому в стрелочных индикаторах (например, в амперметрах) обычно стараются ввести именно критическое затухание, чтобы стрелка успокаивалась максимально быстро для считывания его показаний.

У осциллятора с критическим затуханием добротность равна 0,5. Соответственно, добротность указывает характер поведения осциллятора. Если добротность больше 0,5, то свободное движение осциллятора представляет собой колебания; теоретически, со временем он пересечёт положение равновесия неограниченное количество раз. Добротность, меньшая или равная 0,5, соответствует неколебательному движению осциллятора; в свободном движении он пересечёт положение равновесия не более одного раза.

Добротность иногда называют коэффициентом усиления осциллятора, так как при некоторых способах возбуждения при совпадении частоты возбуждения с резонансной частотой колебаний их амплитуда устанавливается примерно в Q{\displaystyle Q} раз больше, чем при возбуждении с той же интенсивностью на низкой частоте.

Также добротность примерно равна количеству колебательных циклов, за которое амплитуда колебаний уменьшается в e{\displaystyle e} раз, умноженному на π{\displaystyle \pi }.

В случае колебательного движения затухание ещё характеризуют такими параметрами, как:

• Время жизни колебаний (оно же время затухания, оно же время релаксации) τ — время, за которое амплитуда колебаний уменьшится в e раз.

τ=1/γ.{\displaystyle \tau =1/\gamma .}

Это время рассматривается как время, необходимое для затухания (прекращения) колебаний (хотя, формально, свободные колебания продолжаются бесконечно долго).

• Логарифмический декремент затухания. Определяется как логарифм отношения двух последовательных максимальных отклонений в одну сторону: d=ln⁡(xmaxn/xmaxn+1).{\displaystyle d=\operatorname {ln} (x_{{\text{max}}\;n}/x_{{\text{max}}\;n+1}).} Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.

Замечание о вынужденных колебаниях гармонического осциллятора[править | править код]

Колебания осциллятора называют вынужденными, когда на него производится некоторое дополнительное воздействие извне. Это воздействие может производиться различными средствами и по различным законам. Например, силовым возбуждением называется воздействие на груз силой, зависящей только от времени по определённому закону. Кинематическим возбуждением называют воздействие на осциллятор движением точки закрепления пружины по заданному закону. Возможно также воздействие трением, когда, например, среда, с которой груз испытывает трение, совершает движение по заданному закону.

Бутиков Е. И. Собственные колебания линейного осциллятора. Учебное пособие

1. ↑ Решение приведённого дифференциального уравнения можно записать как с помощью функции синуса:

   x(t)=Asin⁡(ωt+φ){\displaystyle x(t)=A\sin(\omega t+\varphi )},

   так и через косинус:

   x(t)=Acos⁡(ωt+φ){\displaystyle x(t)=A\cos(\omega t+\varphi )}.

   Оба варианта верны, поскольку известно общее равенство cos θ = sin(π/2 — θ). Используя тригонометрические соотношения, можно записать

   Acos⁡(ωt+φ)=Acos⁡(φ)cos⁡(ωt)−Asin⁡(φ)sin⁡(ωt),{\displaystyle A\cos(\omega t+\varphi )=A\cos(\varphi )\cos(\omega t)-A\sin(\varphi )\sin(\omega t),}

   и таким образом

   acos⁡(ωt)+bsin⁡(ωt){\displaystyle a\cos(\omega t)+b\sin(\omega t)}

   также является верным решением при соответствующим образом выбранных постоянных a и b.