ПРИМЕРЫ РАСЧЕТА ПРОЧНОСТИ СВАРНЫХ СОЕДИНЕНИЙ
Пример 1. Определить длину швов, прикрепляющих уголок 100x100x10 мм к косынке (рис. 11. а). Соединение конструируется равнопрочным целому элементу. Материал сталь Ст2. Электроды Э42.
В табл. 2 для стали Ст2 находим допускаемое напряжение [σp] = 140 МПа. Площадь профиля уголка 1920 мм² («Уголки стальные горячекатаные равнополочные» ГОСТ 8509-93).
Расчетная сила в уголке
Р = 140×1920 = 268 800 Н
В данном случае допускаемое напряжение при срезе, согласно табл. 1, в сварном шве
[τcp] = 140×0,6 = 84 МПа
.
Требуемая длина швов (при К =10 мм) в нахлесточном соединении согласно расчету к рис. 11а.
Длина лобового шва l = 100 мм: требуемая длина обоих фланговых швов lфл = 458-100 = 358 мм. Так как для данного уголка е1 = 0,7l то длина шва 2 будет l2 — 0,7×358 = 250 мм, длина шва 1 будет l Принимаем l2 = 270 мм, l1 = 130 мм.
Принимаем l2 = 270 мм, l1 = 130 мм.
Пример 2. Определить длину l швов, прикрепляющих швеллер №20а. нагруженный на конце моментом М = 2,4×107 Н·мм (рис. 11. б). Материал сталь Ст2. Электроды Э42.
В табл. 2 для стали Ст2 находим допускаемое напряжение [σp] = 140 МПа. Допускаемое напряжение при срезе, согласно табл. 1, в сварном шве
[τ’cp] = 140×0,6 = 84 МПа
.
Момент сопротивления сечения швеллера W = 1,67 x 105 мм³ (из ГОСТа)
Напряжение
σ = 2,4×107 / 1,67×105 = 144 МПа
Катет горизонтальных швов К1 = 10 мм, вертикального К2 = 7,5 мм. Из формулы 1 (см. выше) находим
Принимаем l = 200 мм. При этой длине шва напряжение при изгибе
Полученная величина меньше допускаемой [τ’cp] = 84 МПа.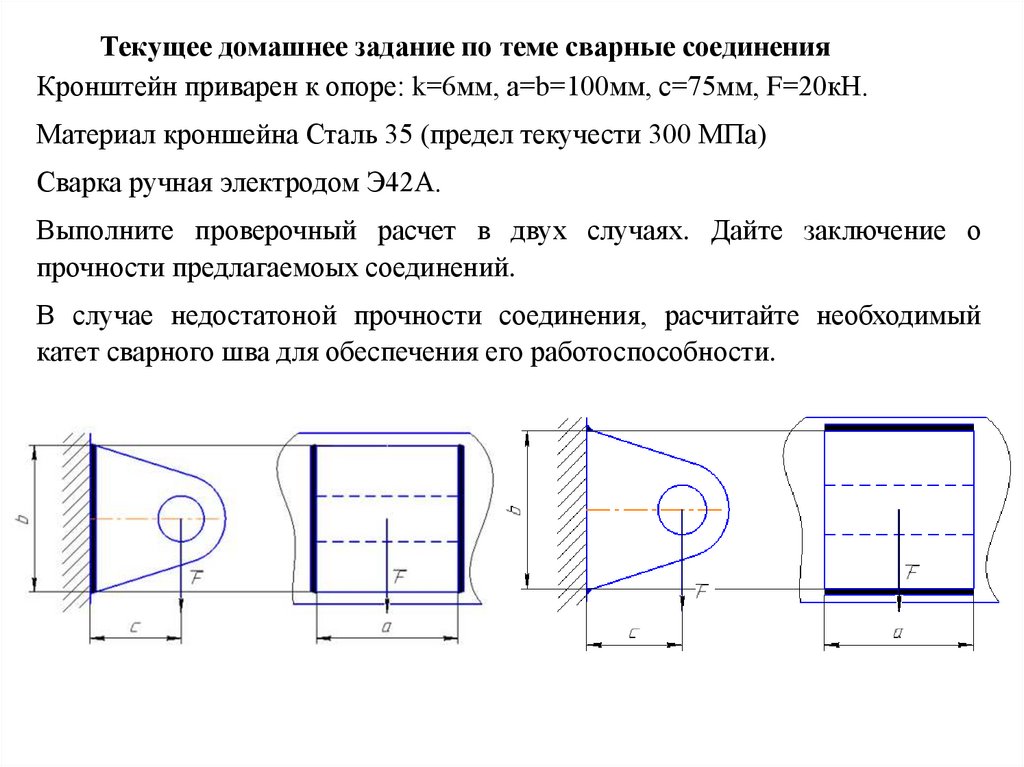
ЭЛЕКТРОДЫ
Размеры и общие технические требования на покрытые металлические электроды для ручной дуговой сварки сталей и наплавки поверхностных слоев из сталей и сплавов приведены в ГОСТ 9466-75 или кратко здесь.
Электроды покрытые металлические для ручной дуговой сварки конструкционных и теплоустойчивых сталей (по ГОСТ 9467-75):
Электроды изготовляют следующих типов:
Э38, Э42, Э46 и Э50 — для сварки низкоуглеродистых и низколегированных конструкционных сталей с временным сопротивлением разрыву до 500 МПа:
Э42А, Э46А и Э50А — для сварки углеродистых и низколегированных конструкционных сталей с временным сопротивлением разрыву до 500 МПа, когда к металлу сварных швов предъявляют повышенные требования по пластичности и ударной вязкости;
Э55 и Э60 — для сварки углеродистых и низколегированных конструкционных сталей с временным сопротивлением разрыву св. 500 до 600 МПа;
Э70, Э85, Э100, Э125, Э150 — для сварки легированных конструкционных сталей повышенной и высокой прочности с временным сопротивлением разрыву свыше 600 МПа;
Э-09М, Э-09МХ, Э-09Х1М, Э-05Х2М, Э-09Х2МГ, Э-09Х1МФ, Э-10Х1М1НФБ, Э-10ХЗМ1БФ, Э-10Х5МФ — для сварки легированных теплоустойчивых сталей.
Механические свойства металла шва,
наплавленного металла и сварного соединения при нормальной температуре (по ГОСТ 9467-75)
| Типы электродов | Металл шва или наплавленный металл | Сварное соединение, выполненное электродами диаметром менее 3 мм | |||
| Временное сопротивление разрыву σв, МПа (кгс/мм²) | Относительное удлинение δ5, % | Ударная вязкость KCU, Дж/см² (кгс·м/см²) | Временное сопротивление разрыву σв, МПа (кгс/мм²) | Угол загиба, градусы | |
| не менее | |||||
| Э38 | 380 (38) | 28 (3) | 380 (38) | ||
| Э42 | 420 (42) | 78 (8) | 420 (42) | ||
| Э46 | 460 (46) | 78 (8) | 460(46) | ||
| Э50 | 500 (50) | 69 (7) | 500 (50) | ||
| Э42А | 420 (42) | 148 (15) | 420 (42) | ||
| Э46А | 460 (46) | 138 (14) | 460 (46) | ||
| Э50А | 500 (50) | 129 (13) | 500 (50) | ||
| Э55 | 550 (55) | 118 (12) | 550 (55) | ||
| Э60 | 600 (60) | 98 (10) | 600 (60) | ||
| Э70 | 700 (70) | 59 (6) | - | - | |
| Э85 | 850 (85) | 49 (5) | - | - | |
| Э100 | 1000 (100) | 49 (5) | - | - | |
| Э125 | 1250 (125) | 38 (4) | - | - | |
| Э150 | 1500 (150) | 38 (4) | - | - |
ГОСТ 9467-75 предусматривает также типы электродов и механические свойства наплавленного металла или металла шва для легированных теплоустойчивых сталей.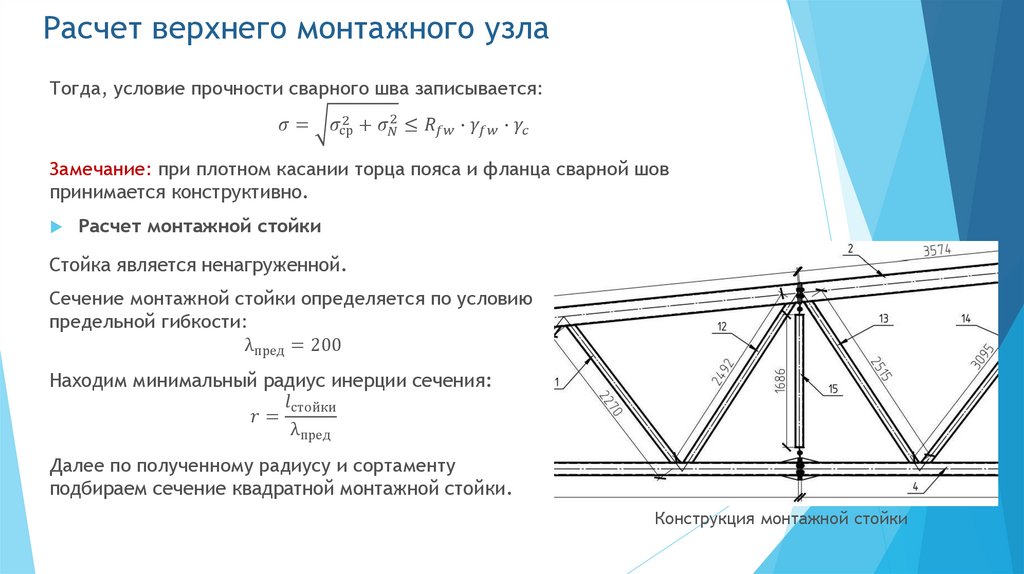
Электроды покрытые металлические для ручной дуговой наплавки
| Тип | Марка | Твердость без термообработки после наплавки HRC | Область применения |
| Э-10Г2 Э-11Г3 Э-12Г4 Э-15Г5 Э-30Г2ХМ | ОЗН-250У O3H-300У ОЗН-350У ОЗН-400У НР-70 | 22,0-30,0 29,5-37,0 36,5-42,0 41,5-45,5 32,5-42,5 | Наплавка деталей, работающих в условиях интенсивных ударных нагрузок (осей, валов автосцепок, железнодорожных крестовин, рельсов и др.) |
| Э-65Х11Н3 Э-65Х25Г13Н3 | ОМГ-Н ЦНИИН-4 | 27,0-35,0 25,0-37,0 | Наплавка изношенных деталей из высокомарганцовистых сталей типов Г13 Г13Л |
| Э-95Х7Г5С Э-30Х5В2Г2СМ | 12АН/ЛИВТ ТКЗ-Н | 27,0-34,0 51,0-61,0 | Наплавка деталей, работающих в условиях интенсивных ударных нагрузок с абразивным изнашиванием |
| Э-80Х4С Э-320Х23С2ГТР Э-320Х25С2ГР Э-350Х26Г2Р2СТ | 13КН/ЛИВТ Т-620 Т-590 Х-5 | 57,0-63,0 56,0-63,0 58,0-64,0 59,0-64,0 | Наплавка деталей, работающих в условиях преимущественно абразивного изнашивания |
| Э-300Х28Н4С4 Э-225Х10Г10С Э-110Х14В13Ф2 Э-175Б8Х6СТ | ЦС-1 ЦН-11 ВСН-6 ЦН-16 | 49,0-55,5 41,5-51,5 51,0-56,5 53,0-58,5 | Наплавка деталей, работающих в условиях интенсивного абразивного изнашивания ударными нагрузками |
ГОСТ предусматривает также и другие химический состав, типы и марки электродов.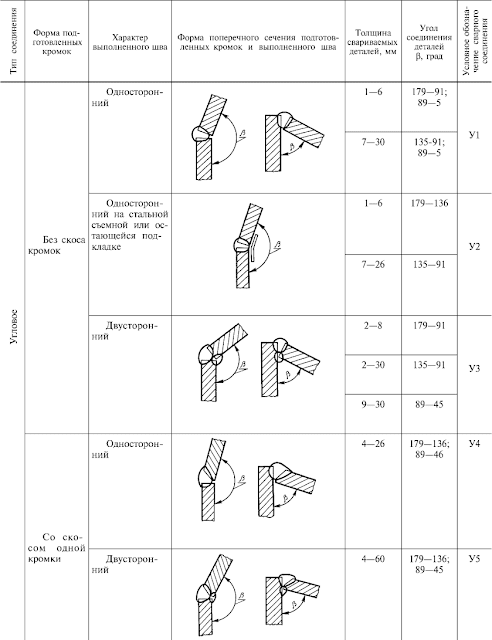
Сварочные материалы, применяемые для сварки стальных конструкций, должны обеспечивать механические свойства металла шва и сварного соединения (предел прочности, предел текучести, относительное удлинение, угол загиба, ударную вязкость) не менее нижнего предела свойств основного металла конструкции.
Свариваемые материалы и применяемые электроды:
— СтЗкп, СтЗкп, СтЗпс, Сталь 08кп, Сталь 10 — Э42, Э42А, Э46;
— Сталь 20 — Э42;
— Сталь 25Л — Э46;
— Сталь 35Л, Сталь 35, Сталь 45, Ст5кп, Ст5пс — Э50А;
— Сталь 20Х, Сталь 40X — Э85;
— Сталь 18ХГТ, Сталь 30ХГСА — Э100;
— АД1, АД1М, АМг6 — Присадочные прутки.
Дата добавления: 2016-05-28; просмотров: 6293; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Соединения внахлестку — Типы сварных соединений. Расчет соединений при действии осевых сил — Сварные соединения
Соединение внахлестку может осуществляться с накладками и без них при помощи угловых швов.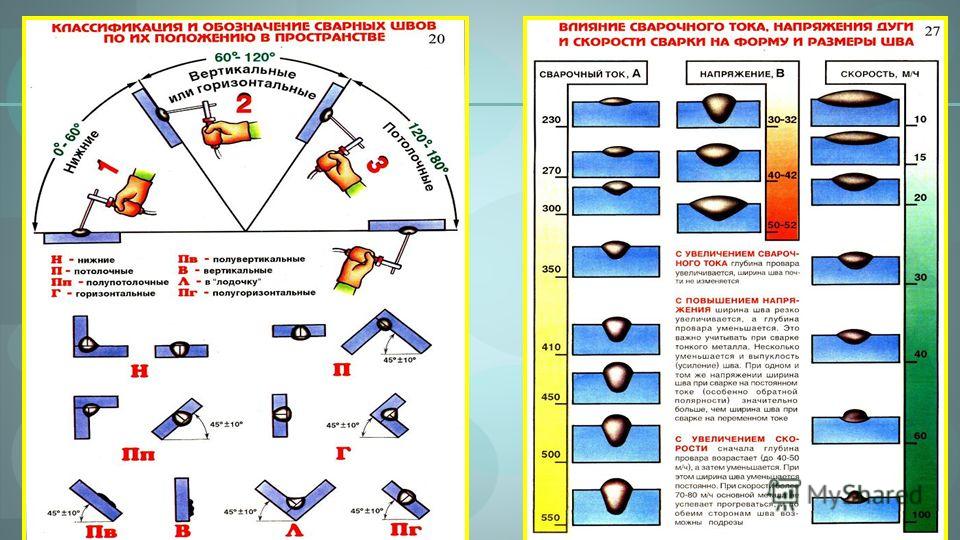
В зависимости от расположения по отношению к действующим усилиям угловые швы могут быть: фланговые (расположенные параллельно усилию) и лобовые или торцовые (расположенные перпендикулярно усилию).
Простейшим соединением этого типа является конструкция, показанная на фигуре. Передача усилия в нем с одного элемента на другой протекает весьма неравномерно как по длине шва, так и по поперечному сечению соединения. На фигуре, а показан поток силовых линий, концентрирующихся у концов швов, а на фигуре, б — диаграмма распределения напряжений по длине шва.
Соединения с фланговыми швами
Опытами и теоретическими исследованиями доказано, что чем длиннее шов, тем больше неравномерность пере дачи усилия по его длине. Однако при статической нагрузке и при не очень длинных швах после достижения в крайних точках швов напряжений, равных пределу текучести, при дальнейшем нагружении неравномерность в распределении напряжений по длине шва уменьшается, эпюра напряжений выравнивается и раз рушение происходит по всей длине шва путем среза по поверхности, характеризуемой линией АВ.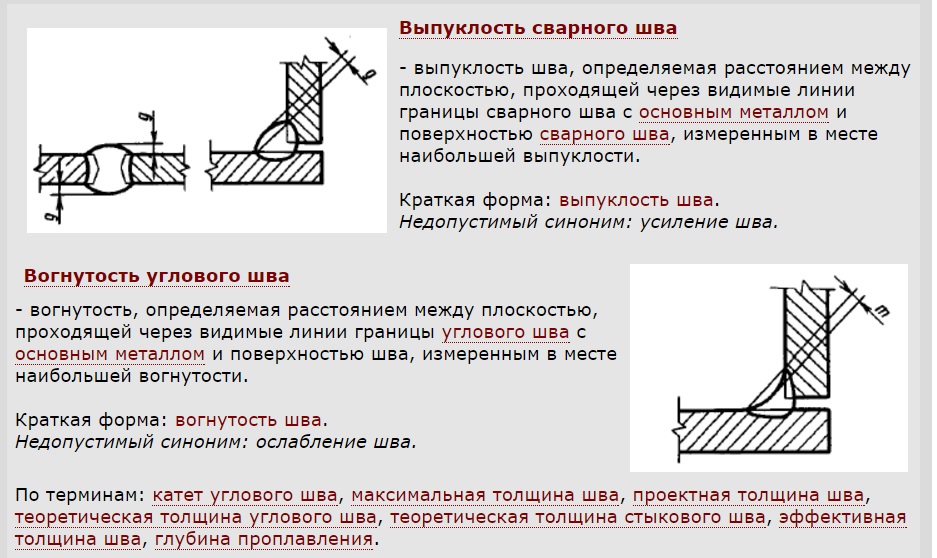
Эта линия имеет криволинейные участки в начале и конце (у наиболее напряженных точек) и прямолинейный участок по середине шва. Такой вид разрушения позволяет положить в основу расчета допущение о равномерном распределении напряжений среза по минимальной площади сечения шва, проходящей через наименьшую высоту условного треугольника шва (без учета наплыва, фигуре, г).
При равных катетах шва эта высота равняется
где через hш обозначен размер катета (толщина) шва. Таким образом, площадь среза фланговых угловых швов будет, равна
где ∑lш — сумма расчетных длин сварных швов.
Из-за наличия непровара вначале и кратера в конце шва, а также из-за большего влияния случайных включений на малой длине шва, где трудно обеспечить хороший провар его, наши нормы и технические условия не разрешают, чтобы расчетная длина шва была меньше 40 мм или меньше 4hш.
Предположение о равномерной работе фланговых швов будет I неправильным при очень длинных швах, так как возможно достижение предела прочности в точках А и В раньше, тем выровняются напряжения по всей длине шва.
Поэтому НиТУ ограничивают наибольшую расчетную длину фланговых швов в соединениях длиной, равной l ≤ 60hш за исключением сопряжений, где усилие, воспринимаемое фланговым швом, возникает на всем его протяжении (например, поясные швы балки). В последнем случае длина флангового шва не ограничивается. I Прочность фланговых швов зависит также от их толщины, причем с увеличением катета шва предел прочности их несколько падает.
Толщина шва также нормируется и принимается не белее 1,5δ в конструкциях, работающих под статической нагрузкой, и 1,2δ — в конструкциях, работающих под динамической нагрузкой (δ — наименьшая толщина соединяемых элементов). Желательно при проектировании избегать применения швов толщиной более 20 — 25 мм. Минимальная толщина швов принимается равной 4 мм.
Расчет соединения внахлестку с фланговыми швами, находящегося под воздействием осевой силы, при принятом допущении о равномерном распределении касательных (срезывающих) напряжений тшпроизводится по формуле
где N — расчетная нормальная (осевая) сила в кг;
hш — толщина (катет) шва в см;
lш — расчетная длина шва в см;
Rсву — расчетное сопротивление срезу сварного углового шва в кг/см2, принимаемое по таблице Расчетные сопротивления сварных швов в кг/см;
m — коэффициент условий работы конструкции или элемента.
Обычно толщину шва hш назначают равной толщине соединяемых элементов или несколько меньше ее; таким образом, рас четом определяется необходимая минимальная суммарная дли на швов, которая получается по формуле
Конструктивная длина шва должна быть больше расчетной да 10 — 20 мм, чтобы компенсировать образование кратера на конце шва и не всегда хороший провар в начале шва.
Пример 1. Требуется рассчитать стык двух листов из стали марки Ст. 3, сечением 250 X 12 мм на растягивающее расчетное усилие N = 56,7 т. Конструкция стыка запроектирована с двумя накладками, приваренными фланговыми швами. Коэффициент условий работы элемента m = 1.
Расчет стыка двух листов из стали
Решение.
1. Назначаем необходимое сечение накладок. Очевидно, что площадь сечения двух накладок (2Fн) должна равняться основному сечению листа (Fл) или быть несколько больше его, иначе усилие N не сможет быть передано с одного листа на другой, т. е. должно быть 2Fн ≥ Fл.
е. должно быть 2Fн ≥ Fл.
Конструктивно назначаем сечение накладок 200 X 8 мм; тогда
2Fн = 2 * 20 * 0,8 = 32 см2, Fл = 25 * 1,25 * 30 см2;
таким образом, 2Fн > Fл.
2. Назначаем тип электрода Э42.
Тогда расчетное сопротивление срезу сварного углового шва будет со гласно таблице Расчетные сопротивления сварных швов в кг/см равняться Rсву = 1400 кг/см2. Для накладок толщиной 10 мм принимаем фланговые швы толщиной hш =8 мм.
3. Находим суммарную расчетную длину швов с одной стороны стыка по формуле (4. IV)
4. Находим длину стыковой полунакладки. По одну сторону стыка две полунакладки привариваются четырьмя фланговыми швами. Следовательно, расчетная длина одного шва должна быть не меньше
Конструктивную длину шва следует назначить несколько большей, учитывая кратер в конце шва и возможный непровар в начале шва, а также зазор между листами и необходимость округления проектного размера до практически удобной цифры.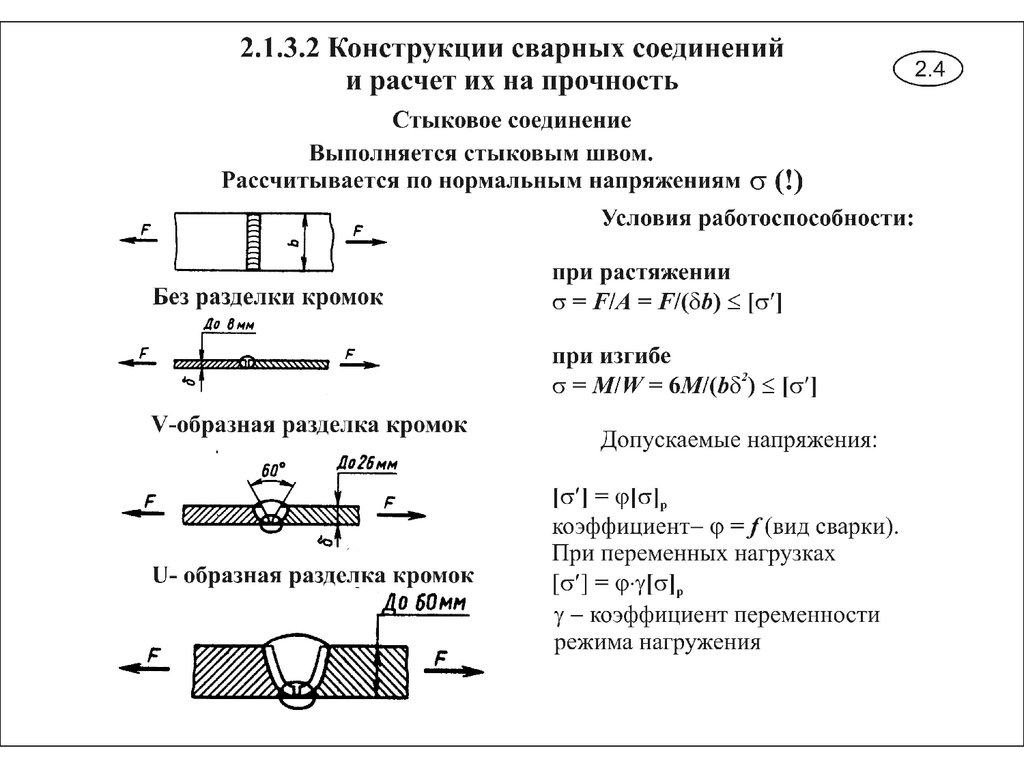
Назначаем конструктивную длину шва
5. Принимаем две стыковые накладки сечением 200 X 8 мм, длиной lш = 200 * 2 = 400 мм; толщина шва hш=8 мм.
При прикреплении фланговыми швами несимметричного сечения, например двух уголков к листу, необходимо учитывать неравномерное распределение усилия, действующего, в соединении, между швами, передающими силовой поток с уголков на лист.
Растягивающую уголки силу N можно рас сматривать как равнодействующую силового потока нормальных напряжений, приложенную в центре тяжести сечений уголков.
Несимметричное соединение внахлестку
Линия центров тяжести проходит несимметрично относительно сварных швов, расположенных у обушка и пера уголка. Поэтому площадь сечений швов у обушка и пера уголка также должна быть различной в соответствии с распределением силового потока.
Очевидно, что усилие N распределится обратно пропорционально расстояниям сварных швов до линии центра тяжести уголка, которая проходит на расстоянии от обушка, близком к 1/3 ширины полки.
Поэтому распределение усилия N может приниматься следующее:
Тогда формула, определяющая расчетную длину ∑l1 прикрепления уголков у обушка, получится из формулы
где hш — толщина шва у обушка.
Поскольку усилие со стороны пера уголка значительно меньше, шов у пера мог бы быть прерывистым. Однако обычно этот шов заваривают по всей длине пера, причем часто его принимают меньшей толщины. Обрезать полку уголка для уменьшения длины шва l2 не рационально; уголки (за редким исключением) следует обрезать перпендикулярно оси.
Пример 2. Требуется рассчитать прикрепление двух уголков 75 X 8 к фасонке толщиной δ = 10 мм. Расчетное растягивающее усилие в уголках N = 42,5 г.
Материал — сталь марки Ст. 3; электроды типа Э42. Коэффициент условий работы m = 1.
Расчет прикрепления двух углов к фасонке
Решение. Определяем расчетную длину l1 по формуле (5.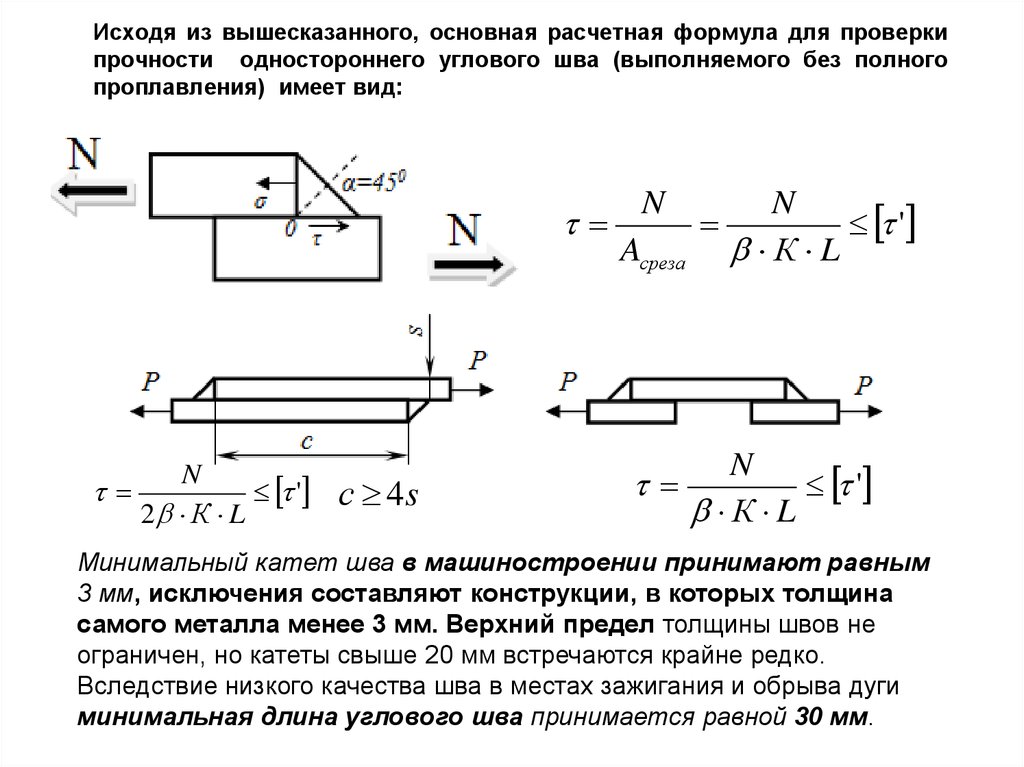 IV), принимая толщину шва hш = 0,8 см. Вследствие наличия двух уголков и соответственно двух швов длиной l1 расположенных у обушков уголков, будем иметь
IV), принимая толщину шва hш = 0,8 см. Вследствие наличия двух уголков и соответственно двух швов длиной l1 расположенных у обушков уголков, будем иметь
Принимаем l1 = 181 + 19 = 200 мм.
При конструировании в случае необходимости можно уменьшить раз меры фасонки, как указано пунктиром на фигуре, учитывая возможное уменьшение длины l2 по сравнению с l1.
Несмотря на некоторые отрицательные качества соединений с фланговыми швами (неравномерность в распределении напряжений), они применяются весьма часто. Причина этого заключается в несколько большей их пластичности по сравнению с другими видами соединений вследствие происходящей во время работы деформации среза, поскольку модуль упругости при сдвиге (G = 840 000 кг/см2) меньше, чем модуль упругости при растяжении (E = 2 100 000 кг/см2).
«Проектирование стальных конструкций»,
К.К.Муханов
|
Заглавная страница
Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 4 из 5Следующая ⇒ При расчете прикрепления уголков угловыми сварными швами учитывают, что усилие, действующее на уголок, прикладывается к его центру тяжести и при приварке уголка к фасонке распределяется между швами, выполненными по обушку и по перу уголка (рис. 3). Распределение усилия происходит пропорционально площадям, отсеченным у уголка на разрезе линией центра тяжести. В равнополочных уголках на швы по обушку приходится 70% усилия, на швы по перу 30%. Соответственно, при одинаковых по высоте катетах шва длина шва по обушку составит 70%, а по перу 30% от обшей длины шва. Общая длина шва определяется по формулам расчета угловых сварных швов. Рис. 3 Высота катета шва kfпо перу уголка обычно принимается меньше на 2 мм толщины уголка t, по обушку уголка высота катета назначается не более 1,2t. 4. Расчет сварных соединений на действие изгибающего момента В случае воздействия изгибающего момента на сварное соединение расчет производится в зависимости от вида сварных швов. 11ри воздействии на стыковые швы момента М в плоскости, перпендикулярной плоскости шва (рис. 8.9, а), расчет выполняется по формуле где Ww − момент сопротивления расчетного сечения шва;
Пример 1. Рассчитать прикрепление двух уголков 100 х 8 к фасонке фермы толщиной t = 10 мм. Уголки и фасонка фермы выполнены из стали С345. На стержень действует растягивающее усилие N =300 кН; γn= 1,0. Сварка ручная электродуговая. Климатический район строительства II4. Решение. 1. Определяем группу конструкции по табл. 50* СНиП II-23-81*: стержень фермы относится ко 2-й группе, а фасонка фермы – к 1-й группе. 2. Принимаем марку электродов: для сварки элементов, относящихся к 1-й группе конструкций и учитывая, что элемент иыполнен из стали С345, по табл. 55* СниП II-23-81* принимаем электроды Э50А. Rwf=215Мпа = 18,0 кН/см2 (табл. 56 СниП II-23-81*). Rwz=0,45Run = 0,45 ∙ 490 = 220,5 Мпа = 22,5 кН/см2 (Run= 490 Мпа – см. табл. 2.2). Рис. 4
3. Принимаем высоту катетов швов одинаковую по перу и по обушку уголков kf=6 мм = 0,6 см; высота катета принята больше минимальной высоты kf,min=5 мм (табл. 38* СНиП II-23-81*). 4. Определяем по табл. 34* СНиП II-23-81* коэффициенты: βf = 0,7;βz =l,0. 5. Устанавливаем для климатического района II4 коэффициенты: γwf = 1,0; γwz= 1,0. 6. Определяем расчетную длину швов по металлу шва:
7. Определяем расчетную длину швов по металлу границы сплавления: 8. Длины швов принимаем по наибольшей длине (в данном случае по металлу шва). Следует учитывать, что эта длина шва требуется для прикрепления двух уголков. Распределяем швы между уголками − по перу (30%) и обушку уголка (70%): Вывод. Принимаем швы с высотой катета kf=6мм; сварка ручная электродуговая; электроды Э42А; распределение швов по обушку и перу уголка.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ №10 Задача 1. Определить длину сварных швов, прикрепляющих уголок к фасонке фермы. Климатический район строительства II4, γc = 0,9. Сварка ручная электродуговая. На стержень из уголка 70 х 6 действует растягивающее усилие N = 100 кН, γn = 0,95; фасонка выполнена толщиной t = 12 мм, сталь С245 (рис. Рис. 5 Таблица 1 Исходные данные
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №11 Тема: Подбор сечения стержней металлической фермы из парных уголков Цель работы — расчёт сжатых и растянутых стержней ферм из двух спаренных уголков на подбор сечения В результате выполнения работы студент должен: ü знать виды ферм, генеральные размеры, некоторые правила конструирования ферм и узлов; ü уметь рассчитать, т. Теоретическое обоснование: 1. Расчет растянутых стержней Растянутые стержни стальных ферм рассчитываются как центрально-растянутые элементы (см. раздел 6). При центральном растяжении должна обеспечиваться прочность и ограничивается гибкость стержня. Требуемая площадь растянутых стержней определяется из формулы при отсутствии ослаблений (отверстий) площадь сечения стержня А = А n,где А n − площадь сечения стержня нетто. Гибкость проверяется по формуле: при статической нагрузке предельная гибкость растянутых поясов и стержней ферм λпред. = 400. 2. Расчет сжатых стержней Сжатые стержни рассчитываются как центрально-сжатые элементы. Порядок расчета сжатых стержней ферм аналогичен расчету центрально-сжатой колонны (см. раздел 5). При центральном сжатии должны быть обеспечены прочность, устойчивость и ограничивается гибкость. В соответствии с расчетом устойчивости требуемая площадь сечения стержня фермы определяется из формулы Гибкость сжатых поясов и стержней ферм проверяется по уравнению (5.4, г)аналогично проверке гибкости растянутых стержней. Предельная гибкость сжатых стержней определяется по табл. 5.4. Пример 1. Подобрать сечение стержня решетки стальной фермы, работающей в климатическом районе II4 (рис. 9.12). На стержень действует растягивающее усилие N =200 кН (нагрузка статическая). Геометрическая длина стержня (расстояние между узлами) l = 3000 мм. Предельная гибкость λmax = 400. Толщина фасонки t =10 мм. Решение. 1. Учитывая климатический район и то, что фермы относятся к конструкциям группы 2 (табл. 2. Находим расчетное сопротивление стали по пределу текучести (табл. 2.2): Ry= 240 МПа = 24,0 кН/см2 (при толщине проката 2−20 мм). 3. Определяем коэффициент условий работы γс = 0,95 (табл. 2.3). 4. Определяем расчетные длины стержня (см. табл. 11 СНиП II-23-81*): расчетная длина в плоскости фермы: расчетная длина в плоскости, перпендикулярной плоскости фермы: 5. Находим требуемую площадь сечения стержня: 6. По сортаменту прокатной угловой стали (Приложение 1, табл. 3) подбираем уголки, при этом учитываем, что сечение стержня состоит из двух уголков; площадь одного уголка будет равна: 7. Проверяем принятое сечение: прочность обеспечена; б) проверяем гибкость: гибкость в пределах норм. Вывод. Принимаем сечение стержня из двух уголков 50 х 50 х 5, сталь С245. Пример 2. Подобрать сечение стержня решетки фермы (рис. 9.12), работающей в климатическом районе II4. На стержень действует сжимающее усилие N = 359 кН (нагрузка статическая). Геометрическая длина стержня l = 4520 мм. Предельная гибкость λmax = 210 − 60α, (см. табл. 5.4). Толщина фасонки t = 10 мм. Решение. 1. Учитывая, что климатический район строительства II4, фермы относятся к конструкциям группы 2 (табл. 50* СНиП II-23-81*), из допускаемых к использованию сталей принимаем сталь С345-1. 2. Находим расчетное сопротивление стали по пределу текучести Rу = 335 МПа = 33,5 кН/см2 (при толщине проката 2−10 мм, табл. 3. Определяем коэффициент условий работы (табл. 2.3): предполагая, что гибкость стержня будет больше 60, принимаем по п. 3 табл. 2.3 γс = 0,8; также для нашего случая подходит коэффициент условия работы по п. 6а табл. 2.3, γс= 0,95; принимаем в расчет меньшее значение коэффициента γс=0,8. 4. Определяем расчетные длины стержня: расчетная длина в плоскости фермы lef,x= 0,8l = 0,8 ∙ 4520 = 3616 мм; расчетная длина в плоскости, перпендикулярной плоскости фермы, lef,y1= l =4520 мм (табл. 11 СНиП II-23-81*). 5. Находим требуемую площадь сечения стержня из формулы устойчивости; для этого предварительно принимаем гибкость стержня λ= 100 и по гибкости находим коэффициент продольного изгиба φ = 0,493 (табл. 5.3): 6. Определяем требуемые радиусы инерции: 7. По сортаменту (Приложение 1, табл. 8. Проверяем принятое сечение: б) по наибольшей гибкости λ =117,59 определяем (табл. 5.3) коэффициент продольного изгиба φ = 0,473; в) находим значение коэффициента α: так как значение коэффициента получилось больше 0,5, принимаем величину коэффициента α = 0,91; г) определяем предельную гибкость: наибольшая гибкость стержня λх= 117,59, что меньше предельной гибкости λmax= 155,4, следовательно, гибкость стержня в пределах нормы; д) проверяем устойчивость: устойчивость обеспечена. Вывод. Принимаем сечение стержня из двух уголков 100 x 8, сталь С345-1. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ №11 Задача 1. Подобрать сечение растянутого стержня решётки стальной фермы. На стержень действует усилие N=…кН, Геометрическая длина стержня l=…мм. Предельная гибкость λ=400. Толщина фасонки t=…мм. Задача 2. Подобрать сечение сжатого стержня решётки стальной фермы. На стержень действует усилие N=…кН. Геометрическая длина стержня l=…мм. Предельная гибкость λmax=210-60α. Толщина фасонки t=…мм.
Таблица 1 Исходные данные
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №12 Тема: Расчёт центрально-загруженного столбчатого фундамента Цель работы — расчёт тела и подбор количества арматуры отдельно стоящего фундамента. В результате выполнения работы студент должен: ü знать о распределении напряжений под подошвой фундамента и в массиве дисперсного грунта, конструкции фундаментов неглубокого заложения; ü уметь рассчитать по материалу тело фундамента, подобрать количество арматуры. Теоретическое обоснование: ⇐ Предыдущая12345Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 628; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Расчёт узлов стальных конструкций компонентным методом конечных элементов
Аннотация
Статья посвящена вопросу расчёта узлов стальных конструкций. Материал статьи содержит краткое описание существующих методик расчёта и их сравнительный анализ. Основные разделы посвящены описанию компонентного метода, используемого в европейской практике, и его модификации – компонентному методу конечных элементов.
Названный метод используется в программе IDEA StatiCa Connection, которая предлагает конструкторам надежный и проверенный инструмент для инженерного анализа, расчёта и проверки по нормам (в том числе российским) узлов стальных конструкций.
Приводятся описания основных принципов и теоретически обоснованных методов, заложенных в реализацию программы. В заключении статьи в качестве примера приводятся расчёт рамного узла по СП 16.13330.2017 средствами IDEA StatiCa Сonnection и сравнительный анализ полученного решения с ручным расчётом.
В заключении статьи в качестве примера приводятся расчёт рамного узла по СП 16.13330.2017 средствами IDEA StatiCa Сonnection и сравнительный анализ полученного решения с ручным расчётом.
1 Расчёт узлов стальных конструкций. Состояние вопроса
Сегодня трудно представить расчёт какой-либо конструкции без использования современных программно-вычислительных комплексов (далее ПВК). По мере развития информационных технологий функциональные возможности ПВК расширяются, позволяя решать более сложные задачи, в том числе с учётом физической, геометрической и конструктивной нелинейности. Широкие возможности ПВК позволяют создавать модели зданий и сооружений, максимально приближенные к реальности – с учётом жёсткости соединений элементов, нелинейной работы материала и др.
В большинстве случаев чрезмерная детализация расчётной схемы и учёт различных типов нелинейности являются неоправданными. Время, затраченное на подготовку расчётной схемы и сам расчёт, не оправдывается избыточной точностью получаемых результатов.
Для того чтобы избежать чрезмерной детализации при расчёте зданий и сооружений, используются различные упрощения расчётной схемы. К примеру, все линейно-протяжённые конструкции – балки, колонны – моделируются стержневыми элементами; плоские элементы – плиты и стены – пластинчатыми элементами или просто нагрузками. Сопряжения элементов друг с другом и конструкций с основанием также описываются упрощённо. Реальные размеры соединений не учитываются, равно как и их жёсткость. Все узлы условно делятся на «жёсткие» (передающие вращательные усилия) и «шарнирные» (не воспринимающими моменты).
Рис. 1-1. Жёсткое (слева) и шарнирное (справа) сопряжение элементов
В пункте 5.1.1 раздела 5 Еврокода 1993-1-8-2009 отмечено, что в расчёте следует учитывать влияние работы соединений на распределение внутренних усилий и моментов в конструкции. В этом же разделе приводится чуть более широкая классификация узлов по типу модели – они делятся на шарнирные, жёсткие и полужёсткие узлы. Зачастую при составлении расчётной схемы здания или сооружения конструкция узлов заранее неизвестна. Она прорабатывается уже после выполнения расчёта. Поэтому может случиться так, что узел, который ранее считался жёстким, после конструирования окажется полужёстким, что, в свою очередь, приведёт к перераспределению усилий. Таким образом, усилия, по которым подбирались диаметры болтов, катеты сварных швов и толщины рёбер жёсткости, могут измениться. По этой причине процесс приходится повторять несколько раз.
Зачастую при составлении расчётной схемы здания или сооружения конструкция узлов заранее неизвестна. Она прорабатывается уже после выполнения расчёта. Поэтому может случиться так, что узел, который ранее считался жёстким, после конструирования окажется полужёстким, что, в свою очередь, приведёт к перераспределению усилий. Таким образом, усилия, по которым подбирались диаметры болтов, катеты сварных швов и толщины рёбер жёсткости, могут измениться. По этой причине процесс приходится повторять несколько раз.
Даже в случае простых схем с небольшим количеством конструктивных элементов процесс может занять довольно много времени – каждый узел должен быть сконструирован должным образом, чтобы воспринять полученные усилия. Использование типовых решений (серии, пособия) может упростить процесс, однако при расчёте конструкций сложной формы зачастую требуется детальная проработка нестандартных узлов.
Рис. 1-2. Типовой (слева) и нестандартный (справа) узлы
Расчёт стандартных узлов (рис. 1-2, слева) можно выполнить вручную – для них существуют различные пособия, серии и нормативные документы. Нестандартные узлы (рис. 1-2, справа) всегда требуют составления сложной наукоёмкой модели, описывающей его поведение в составе конструкции. Обычно расчёт выполняется с помощью ПВК, реализующих МКЭ в чистом виде.
1-2, слева) можно выполнить вручную – для них существуют различные пособия, серии и нормативные документы. Нестандартные узлы (рис. 1-2, справа) всегда требуют составления сложной наукоёмкой модели, описывающей его поведение в составе конструкции. Обычно расчёт выполняется с помощью ПВК, реализующих МКЭ в чистом виде.
При составлении модели узла, как правило, возникают следующие вопросы:
- Поведение материала
При переходе от расчёта модели всей конструкции к расчёту узлов всё большее влияние на работу конструкции оказывают локальные эффекты – места изменений сечения, точки приложения сосредоточенных нагрузок и расположение отверстий. Необходимо также учитывать нелинейную работу материала, так как неучёт локальных пластических деформаций приводит к перерасходу материала. Для стали, как правило, используется диаграмма Прандтля – упруго-идеально-пластическая. - Описание модели сварных швов
Способ задания этих элементов в расчётной схеме прямым образом сказывается на результатах. Сварные швы часто заменяются абсолютно жёсткими телами, соединяющими детали или же просто объединением перемещений. И в первом, и во втором случае реальная жёсткость сварного шва не учитывается. Наиболее точным способом будет моделирование сварки при помощи объёмных или плоских конечных элементов, однако в случае нестандартных узлов это может вызвать определённые трудности при построении сетки конечных элементов.
Сварные швы часто заменяются абсолютно жёсткими телами, соединяющими детали или же просто объединением перемещений. И в первом, и во втором случае реальная жёсткость сварного шва не учитывается. Наиболее точным способом будет моделирование сварки при помощи объёмных или плоских конечных элементов, однако в случае нестандартных узлов это может вызвать определённые трудности при построении сетки конечных элементов. - Модель болтов
Самые распространённые модели болта – пространственный стержень и упругая связь между двумя узлами. В такой постановке можно оценить усилия в болтах и сравнить их отклонение от допускаемых усилий. Однако при таком упрощении не учитываются различные факторы локального масштаба – смятие пластин телом болта, сдавливание детали под шайбой и др. Для решения этой проблемы можно использовать объёмные элементы, но это существенно усложнит схему и увеличит время расчёта. - Оценка усилий и напряжений
При моделировании сварных швов объединением перемещений оценка их прочности становится невозможной. Хотя именно в них зачастую развиваются пластические деформации. Если сварные швы задавать объёмными элементами, то для оценки несущей способности шва придётся анализировать большое количество данных – величины нормальных и касательных напряжений в каждом конечном элементе.
Хотя именно в них зачастую развиваются пластические деформации. Если сварные швы задавать объёмными элементами, то для оценки несущей способности шва придётся анализировать большое количество данных – величины нормальных и касательных напряжений в каждом конечном элементе. - Учёт конструктивной нелинейности и локальных эффектов
При большом количестве соприкасающихся поверхностей моделирование контактов становится сложной задачей. Для этого требуется задавать специальные конечные элементы, работающие только на сжатие. Это справедливо также и для зон контакта шайбы и пластины в составе болтового соединения.
Способ решения всех этих вопросов прямым образом сказывается на корректности результатов. Используемые модели должны отражать реальное поведение составных частей узла. В российских нормах отсутствуют чёткие рекомендации по использованию моделей, назначению жесткостей элементов и предельного уровня пластических деформаций в узле. В этом случае приходится руководствоваться общими положениями механики. Для получения достоверных и надёжных результатов необходимо проводить верификацию и валидацию расчётных моделей путём сопоставления с результатами натурных испытаний.
Для получения достоверных и надёжных результатов необходимо проводить верификацию и валидацию расчётных моделей путём сопоставления с результатами натурных испытаний.
2 Зарубежная практика расчёта стальных узлов. Компонентный метод конечных элементов
В зарубежной практике расчёта соединений стальных конструкций широкое распространение получил компонентный метод (далее КМ). Суть его заключается в том, что узел рассматривается как совокупность связанных друг с другом элементов – компонентов. Для заданного узла по определённым правилам строится расчётная модель, состоящая из упругих связей и стержневых элементов, воспринимающих продольные, поперечные, изгибные и крутильные деформации. На рисунке ниже каждому компоненту (стержню или пружине) соответствует своя цифра:
- Стенка колонны, работающая на срез
- Стенка колонны, работающая на сжатие
- Полка и стенка балки, работающие на сжатие
- Полка колонны, работающая на изгиб
- Болты, воспринимающие растяжение
- Фланец, воспринимающий изгиб
- Стенка колонны, работающая на растяжение
Рис.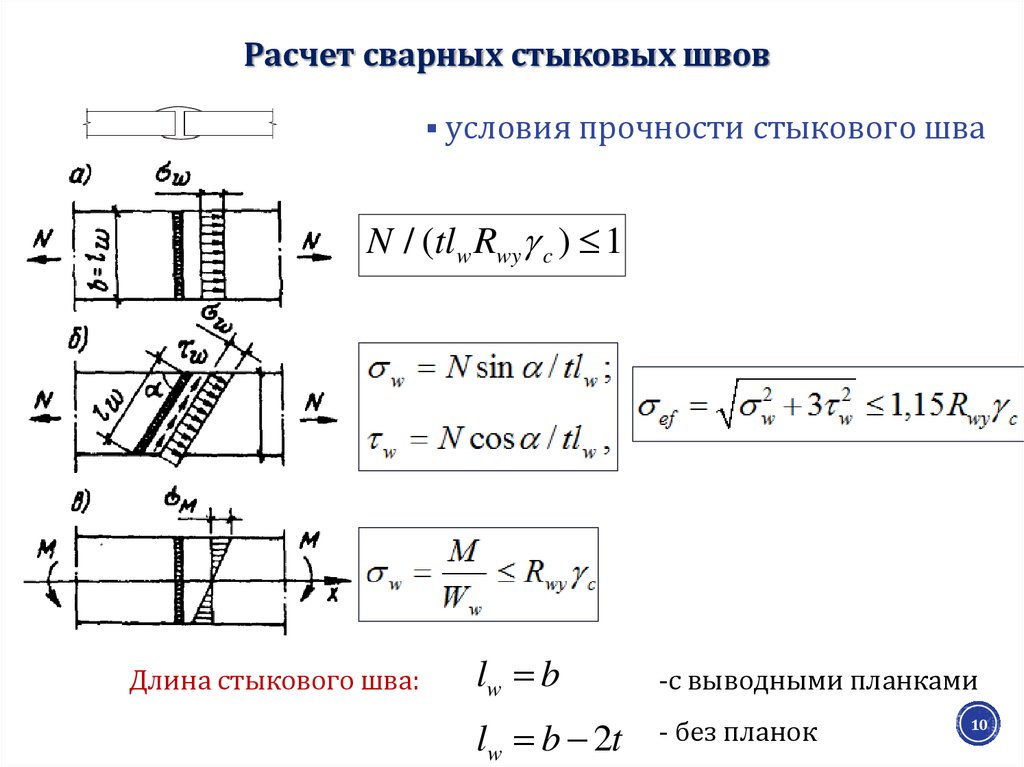 2-1. Компонентная модель узла
2-1. Компонентная модель узла
В результате расчёта в каждом компоненте находятся усилия и напряжения, которые в дальнейшем могут быть использованы для необходимых проверок узла (на прочность, устойчивость и др.) в соответствии с требуемыми нормами проектирования.
Компонентный метод используется в качестве основного в европейских нормативных документах (EN 1993-1-8-2009). Он значительно упрощает процесс расчёта типовых узлов – для них может использоваться единая компонентная модель, элементы которой будут иметь различные физико-механические характеристики, но одинаковое взаимное расположение. При небольших изменениях топологии узла его компонентную модель также придётся менять. Этот факт является основным недостатком этого метода – он имеет существенные ограничения при расчёте узлов произвольной формы.
Этого недостатка лишён метод конечных элементов (далее – МКЭ), позволяющий решать практически любые задачи, с которыми сталкиваются инженеры, – от линейных расчётов плоских рам и балок на статические нагрузки до динамических нелинейных расчётов сложных систем в трёхмерной постановке. Сложная, иногда неправильная форма расчётной области в данном случае не имеет особого значения – она разбивается на простые составляющие – прямые стержни, пластины, тетраэдры и т. д., работа которых описывается известными физическими законами и геометрическими уравнениями.
Сложная, иногда неправильная форма расчётной области в данном случае не имеет особого значения – она разбивается на простые составляющие – прямые стержни, пластины, тетраэдры и т. д., работа которых описывается известными физическими законами и геометрическими уравнениями.
Рис. 2-2. Примеры разбивки схем на конечные элементы
Если КМ дополнить МКЭ, это позволит моделировать узлы, не ограниченные стандартными шаблонами, а жёсткость отдельных компонентов будет вычисляться автоматически исходя из их геометрических и механических свойств. Эта идея принадлежит профессору Франтищеку Уайльду, заведующему кафедрой стальных и деревянных конструкций Чешского технического университета в Праге.
Изначально данная методика разрабатывалась кафедрой стальных и деревянных конструкций факультета Гражданского строительства Чешского технического университета в Праге и факультетом металлических и деревянных конструкций Технологического университета в Брно в рамках гранта на научно-исследовательскую работу. Для расчёта узлов требовался подход, сочетающий в себе базовые положения КМ и универсальность МКЭ. Позднее он получил название компонентного метода конечных элементов – КМКЭ (в оригинале – Component Based Finite Element Method, CBFEM).
Для расчёта узлов требовался подход, сочетающий в себе базовые положения КМ и универсальность МКЭ. Позднее он получил название компонентного метода конечных элементов – КМКЭ (в оригинале – Component Based Finite Element Method, CBFEM).
Модель узла в КМКЭ обладает следующими преимуществами:
- Универсальность
КМКЭ подходит для большинства соединений различной конфигурации – опорных и рамных узлов, узлов покрытия и других узлов, распространённых в инженерной практике. - Удобство и быстрота работы с моделью
Результаты привычных расчётов можно получить за меньшее время по сравнению с другими подходами. - Наглядность
КМКЭ модель даёт современному инженеру достаточное количество информации о поведении узла, его напряжённо-деформированном состоянии и коэффициентах использования отдельных компонентов, а также результатах общих проверок.
Немного позднее разработками университета заинтересовалась компания IDEA StatiCa, и КМКЭ был заложен в основу нового программного обеспечения IDEA StatiCa, предназначенного для расчёта и проверки по нормам узлов стальных конструкций.
3 Программа IDEA StatiCa – инструмент на основе КМКЭ
Основной целью при разработке КМКЭ являлось получение модели узла, максимально приближенной к реальности. Одновременно с этим модель должна быть простой с точки зрения оценки результатов. В процессе разработки моделей компонентов, реализованных сейчас в IDEA StatiCa, было выполнено большое количество тестовых расчётов, натурных и численных экспериментов. Результаты этой работы собраны в книгу «Benchmark cases for advanced design of structural steel connections», написанной профессором Франтищеком Уальдом в соавторстве с Любомиром Шабаткой, генеральным директором компании IDEA StatiCa, и другими. Ознакомиться с этим материалом также можно здесь. Ниже приводится краткое описание моделей пластин, болтов и сварных швов, используемых в IDEA StatiCa.
- Модель материала
Для описания поведения материала, как правило, используются следующие модели: упруго-идеально-пластическая, идеально-упругая с упрочнением и истинная зависимость напряжений от деформации. В IDEA StatiCa для стали используется диаграмма Прандтля с небольшим наклоном вверх ветви, отвечающей за текучесть (показана серым цветом на рисунке 3-1). Критерий наступления предельного состояния связывается с достижением главной продольной деформации максимальной величины.
В IDEA StatiCa для стали используется диаграмма Прандтля с небольшим наклоном вверх ветви, отвечающей за текучесть (показана серым цветом на рисунке 3-1). Критерий наступления предельного состояния связывается с достижением главной продольной деформации максимальной величины.
Рис. 3-1. Диаграммы работы стали
- Пластины и элементы. Сетка конечных элементов
Стенки и полки элементов, рёбра жёсткости, вуты и т. д. моделируются трёх- и четырёхузловыми конечными элементами оболочек с 6 степенями свободы в каждом узле (3 поступательных и 3 вращательных). Каждый элемент имеет 5 точек интегрирования по толщине, в каждой из которых в результате расчёта определяются нормальные и касательные напряжения и отслеживается момент момент наступления текучести.
Генерация сетки конечных элементов отдельно взятой пластины не зависит от других пластин. На конфигурацию сетки КЭ влияет расположение болтов, отверстий и вырезов. Разбивка происходит автоматически по заданным параметрам – максимальному и минимальному размеру КЭ (по умолчанию 50 мм и 10 мм соответственно).
Рис. 3-2. Пример разбивки пластин на конечные элементы
- Контактные поверхности
Контактные зоны между пластинами существенно влияют на распределение напряжений между элементами узла. Решатель автоматически определяет узлы расчётной схемы, проникающие в соседние пластины, и вычисляет распределение контактных напряжений между этими узлами и пластинами. Это позволяет создавать контактные зоны с разной сеткой на пластинах (рис. 3-3).
Рис. 3-3. Работа контактных зон между стенками и поясами Z-образных профилей
Рис. 3-4. Модель сварного шва в IDEA StatiCa
Рис. 3-5. Виды сварных швов. Слева направо: непрерывные, частичные и прерывистые
- Обычные болты
Болты моделируются нелинейными упругими связями, воспринимающими растяжение и срез. В окрестностях отверстия от болта на пластину передаются только сжимающие усилия. Это осуществляется при помощи специальных интерполяционных вставок между узлами тела болта и узлами краёв отверстий. Отверстия под болты по умолчанию назначаются круглыми, но могут быть и овальными – в этом случае болты могут свободно смещаться вдоль длинной стороны, не воспринимая поперечных усилий в этом направлении. После выполнения расчёта в каждом болте отображаются растягивающие и срезающие усилия.
Это осуществляется при помощи специальных интерполяционных вставок между узлами тела болта и узлами краёв отверстий. Отверстия под болты по умолчанию назначаются круглыми, но могут быть и овальными – в этом случае болты могут свободно смещаться вдоль длинной стороны, не воспринимая поперечных усилий в этом направлении. После выполнения расчёта в каждом болте отображаются растягивающие и срезающие усилия. - Болты с предварительным натяжением
Поведение таких болтов при растяжении аналогично обычным болтам с учётом усилия затяжки. Сдвигающее усилие в соединениях с преднапряжёнными болтами воспринимается не смятием пластин, а трением между ними (болто-контактом). В IDEA StatiCa выполняется проверка фрикционных соединений на восприятие сдвигающего усилия болтоконтактом. Если наблюдается проскальзывание, преднапряжённые болты не проходят проверку по деформациям. - Анкерные болты
Анкерные болты используются, как правило, в опорных узлах (рис. 3-6). Они моделируются по тем же принципам, что и обычные. Отличие лишь в том, что анкерный болт с одного конца закрепляется в бетоне. Его длина определяется как сумма толщин шайбы, опорной плиты, слоя раствора и свободной длины анкера в бетоне.
3-6). Они моделируются по тем же принципам, что и обычные. Отличие лишь в том, что анкерный болт с одного конца закрепляется в бетоне. Его длина определяется как сумма толщин шайбы, опорной плиты, слоя раствора и свободной длины анкера в бетоне.
Рис. 3-6. Опорный узел. Обозначения: 1 – колонна, 2 – подкос, 3 – анкер, 4 – противосдвиговой упор
- Бетонные блоки
При расчёте опорных узлов колонн (рис. 3-6) фундамент моделируется упругим основанием Винклера-Пастернака. Его жёсткость определяется в зависимости от его модуля упругости и высоты.
С помощью IDEA StatiCa можно выполнить расчёт узла в следующих режимах:
- Определение НДС узла
После выполнения этого расчёта IDEA StatiCa выводит изополя напряжений во всех пластинах, усилия во всех болтах и коэффициенты использования отдельных компонентов (болтов, анкеров, сварных швов) по заданным нормам проектирования. - Расчёт узла на устойчивость
В ходе этого расчёта вычисляется критическая нагрузка – выводятся коэффициенты запаса устойчивости по первым шести формам.
- Расчёт жёсткости прикрепления элемента
Этот режим позволяет определить вращательную и продольную жёсткость прикрепления отдельных элементов к узлу. По результатам расчёта можно сделать вывод о том, каким в действительности является узел – жёстким, шарнирным или полужёстким. - Расчёт узла на предельный момент
Позволяет произвести расчёт с учётом образования пластического шарнира в одном из элементов. - Расчёт несущей способности узла
В ходе этого расчёта определяется предельная нагрузка, которая может быть воспринята узлом. Критерием являются образование предельной пластической деформации или коэффициенты использования компонентов, превышающие 100 %. - Расчёт на усталость
Этот режим используется для определения диапазона нормальных и касательных напряжений между двумя загружениями (расчётами). Эти номинальные напряжения в дальнейшем используются для проверок по нормам проектирования.
Для встраивания программы IDEA StatiCa в рабочий BIM-процесс разработан интерфейс, позволяющий импортировать данные из многих известных CAD и FEA программ, таких как Tekla, Advance Steel, Revit, SAP2000, ETABS, Robot и др. Эта возможность существенно упрощает процесс создания модели узла, его расчёт и проверки по нормам. Это особенно удобно при работе со сложными и нестандартными узлами, количество которых даже в небольших моделях может достигать нескольких десятков.
4 Интерфейс IDEA StatiCa Connection. Пример расчёта узла по СП 16.13330.2017
Первое, что видит пользователь, запуская IDEA StatiCa Connection, – диспетчер создания модели узла на главной вкладке (рис. 4-1). Здесь задаются параметры, определяющие тип узла, взаимное расположение его элементов, характеристики используемых болтов, анкеров и сварных швов, марки стали, а также нормы проектирования, по которым будет выполняться проверка компонентов узла – СП 16.13330.2017, Еврокод, американские, канадские или австралийские нормы. Выберем здесь СП 16.13330.2017, сталь С345Б, болты М16 класса 8.8 В и материал сварки – электроды Э50.
Выберем здесь СП 16.13330.2017, сталь С345Б, болты М16 класса 8.8 В и материал сварки – электроды Э50.
Рис. 4-1. Диспетчер создания модели узла. Вкладка «Главная»
После нажатия на кнопку «Создать проект» в правой нижней части окна открывается вкладка ленты «Конструирование», где происходит дальнейшая работа с узлом. Все рёбра жёсткости, сварные швы, болты и подрезки элементов задаются с помощью так называемых «Монтажных операций», понятных любому конструктору.
Рис. 4-2. Интерфейс IDEA StatiCa Connection. Вкладка «Конструирование». Монтажные операции
В свойствах монтажной операции «Торцевая пластина» (в правой части окна на рис. 4-2) назначим катеты сварных швов крепления балки к фланцу (kf = 6 мм для полок и 4 мм для стенки) и катеты сварных швов рёбер жёсткости колонны (kf = 6 мм). Здесь же задаётся тип болтов – доступны как обычные болты, так и болты с предварительным натяжением. Выберем напротив свойства «Передача сдвигового усилия» параметр «Трение». Это значит, что теперь сдвиг в соединении будет восприниматься трением между соединяемыми деталями.
Выберем напротив свойства «Передача сдвигового усилия» параметр «Трение». Это значит, что теперь сдвиг в соединении будет восприниматься трением между соединяемыми деталями.
Коэффициент трения можно задать в настройках – примем его равным 0,42.
Сечение колонны – Дв_20К2 (толщина полки tf = 12,0 мм), балки – Дв_25Б2 (толщина полки tf = 9 мм), толщина рёбер жёсткости – 9 мм.
Приложим нагрузки – поперечную силу Vz = -40 кН и изгибающий момент M = 10 кНм и перейдём на вкладку «Проверка». Нажав на кнопку «Расчёт», выполним упругопластический расчёт с учётом физической нелинейности материала и проанализируем полученные результаты.
Согласно разделу 14.3 СП 16.13330.2017 преднапряжённые болты М16 класса прочности 8.8 и класса точности В имеют следующие характеристики:
Rbh = 0,7∙Rbun = 0.70∙830 = 581.0 МПа,
Abn = 157 мм2
Тогда по формулам пункта 14. 3.3 СП 16.13330.2017 получим:
3.3 СП 16.13330.2017 получим:
Qbh = Rbh Abh μ/γh = 581 ∙157∙0.42/1.12∙10-3 кН = 34.21 кН,
что полностью соответствует значению, вычисленному в IDEA StatiCa (рис. 4-3).
Рис. 4-3. Результаты расчёта. Нормативные проверки
Помимо срезающих и растягивающих усилий в результатах расчёта приводятся коэффициенты использования отдельных компонентов в соответствии с выбранными нормами – болтов, сварных швов и т. д. Создание, расчёт узла и вывод результатов занимают всего несколько минут.
Проверка сварных швов выполняется по двум сечениям – металлу шва и металлу границы сплавления (рис. 4-4). Для каждого КЭ сварки вычисляется приведённое сдвигающее усилие, которое подставляется в формулу из пункта 14.1.16. Все параметры швов (длины, катеты, расчётное сопротивление) берутся из модели узла в IDEA StatiCa.
Рис. 4-4. Проверка сварного шва по металлу шва (слева) и металлу границы сплавления (справа)
4-4. Проверка сварного шва по металлу шва (слева) и металлу границы сплавления (справа)
Произведём аналогичный расчёт на действие только продольной силы N = 100 кН и проанализируем растягивающие усилия в болтах.
Результаты численного расчёта в IDEA StatiCa приводятся на рис. 4-5. Сумма продольных усилий составляет 30,8 + 30,6 + 31,0 + 30,8 = 123,2 кН и превышает заданное значение в 100 кН, так как при расчёте в IDEA StatiCa учитывается жёсткость фланца – здесь имеет место «рычажный» эффект.
5 Заключение
В настоящее время IDEA StatiCa Connection является единственным в РФ программным продуктом для автоматизированного расчёта узлов компонентным методом конечных элементов. Программа полностью переведена на русский язык, локализована и имеет сертификат соответствия. Благодаря обширной библиотеке встроенных шаблонов, интуитивно понятному и профессионально проработанному интерфейсу создание, расчёт и проверка узла по нормам занимают всего несколько минут. Наличие прямого взаимодействия с другими CAD и FEA программами для проектирования и расчётов, такими как Tekla, Advance Steel, Revit, SAP2000, ETABS, Robot, позволяет встроить IDEA StatiCa в рабочий BIM-процесс. Программа IDEA StatiCa значительно упрощает работу инженеров-конструкторов, делает её более эффективной и продуктивной, а также обеспечивает высокое качество и надёжность получаемых результатов.
Наличие прямого взаимодействия с другими CAD и FEA программами для проектирования и расчётов, такими как Tekla, Advance Steel, Revit, SAP2000, ETABS, Robot, позволяет встроить IDEA StatiCa в рабочий BIM-процесс. Программа IDEA StatiCa значительно упрощает работу инженеров-конструкторов, делает её более эффективной и продуктивной, а также обеспечивает высокое качество и надёжность получаемых результатов.
Расчет базы колонны. Расчет оголовка колонны
3.3 Расчет базы колонны .
Расчетными элементами базы являются опорная плита и траверсы (рис. 3.3) .
Расчет базы для колонны сплошного сечения производится в следующем порядке.
1. Определяют требуемую площадь опорной плиты
где N = 595,29 кН — расчетное усилие в колонне ;
RВ = 0.75 кН/см2 — прочность бетона на сжатие-для бетона класса В12,5 ;
-площадь верхнего
обреза фундамента .
Поскольку при расчете базы соотношение неизвестно , то коэффициентом задаются в пределах 1,2 … 1,5 . Задаемся для нашего случая
2. Определяется ширина плиты
где — расстояние между траверсами;
— толщина траверсы , принимаемая в пределах 1 … 1.6 см;
C = 8 см-ширина свеса плиты для наложения сварных швов, назначаемая в пределах 5…8см.
3. Определяется длина плиты
Размеры B и L округляют до удобных конструктивных размеров, кратных 2 см. Назначаем длину плиты L = 50 см, а В=50см.
4.Определяется толщина плиты по формуле
где — наибольший изгибающий момент на участках плиты.
Плита базы рассматривается состоящей из нескольких
независимых друг от друга пластинок , отличающихся условиям опирания. Например,
участок , опертый по четырем сторонам ,-1, опертый на три канта ,-2 , и
консольный участок — 3. На каждом из выделенных участков плиты определяется
изгибающий момент.
Участок 1. Максимальный изгибающий момент в середине участка находится по формуле
где — напряжения под плитой базы;
Участок 2. Плита на этом участке закреплена по трем сторонам. Наибольший момент в середине свободной стороны плиты будет равен
где — коэффициент, зависящий от отношения закрепленной стороны () к свободной (), принимаемый по [6] табл.3.3
При соотношении плита рассчитывается как консоль при по формуле
Участок 3 не проверяется, поскольку он имеет меньший консольный свес.
Определяется толщина плиты по максимальному моменту на втором участке
Принимаем толщину плиты .
5. Определяется высота из условия прочности сварных швов, необходимых для передачи усилия со стержня колонны на траверсы .
где 4 — количество угловых швов;
= 0,8 — катет углового шва;
— коэффициент
глубины провара шва , определяемого по табл. 56[1].
56[1].
— расчетное сопротивление углового сварного шва, определяемого по табл.56[1] .
Окончательно высота траверсы:
По сортаменту принимаем 160 мм.
Находится максимально допустимая длина углового сварного шва
6.Определяется катет угловых швов, прикрепляющих траверсы к опорной плите
где — суммарная длина сварных швов.
Принимаем
Проверку прочности траверсы производится как для балки на двух опорах. Пролет траыерсы L=34см
Равномерно распределенная нагрузка: .
; ,
где l1=a2, l2=b1.
Проверка прочности траверсы:
;
где .
3.4 Расчет оголовка колонны .
Наибольшее распространение получил оголовок , изображенный на рис.3.4 , который состоит из плиты и ребер , поддерживающих опорную плиту оголовка и передающих нагрузку на cтержень колонны.
Опорное давление передается с опорной плиты на опорное ребро
, затем на стенку колонны и далее равномерно распределяется по сечению стержня
. Порядок расчета оголовка колонны следующий.
Порядок расчета оголовка колонны следующий.
1. Принимается толщина опорной плиты оголовка в пределах 1.6 … 2,5 см. Назначаем
2. Определяется ширина опорных ребер оголовка
Поскольку в нашем случае в оголовке два опорных ребра, то ширина каждого равна
3. Определяется толщина опорных ребер оголовка
принимаем толщину ребер
где
4. Определяется высота оголвка колнны из условия сварных швов, прикрепляющих ребра к стенкам колонны. Предварительно назначается кактет углового шва
Назначаем , тогда
Назначаем высоту ребер (огловка) с учетом удобных констуктивных размеров, т.е. 16 см
5. Определяется кактет сварных швов, прикрепляющих ребра к плите оголовка,
Такая толщина сварного шва больше максимальной возможной толщины, равной , поэтому для получения нужного размера фрезеруем торец ребра.
6. Производится проверка на срез по формуле
ЛИТЕРАТУРА.
1.СНиП II -23-81*. Стальные конструкции. Нормы проектирования. М., Стройиздат , 1988 г. — 93 с.
2.Металлические конструкции. Общий курс: Учебник для вузов. Под ред. Е.И.Беленя. — 6-е изд.-М., 1985.- 560 с.
3.СНиП II.01.07- Нагрузки и воздействия М. Стройиздат, 1988 г.
4.Справочник конструктора по стальным конструкциям под общей редакцией профессора Н.П. Мельникова. — М., 1965г.
5. Примеры расчета металлических конструкций 2-е издание. Под ред. А. П. Мандрикова М., Стройиздат , 1991 г. –431с.
6. Методические указания к выполнению расчетно-графической работы по курсу “ Металлические конструкции “, Под. ред. А.В.Кропачева.
СОДЕРЖАНИЕ.
СОДЕРЖАНИЕ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ
ЦЕЛЬ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ 1
1. КОМПОНОВКА РАБОЧЕЙ ПЛОЩАДКИ 1
1. 1
Выбор схем балочных клеток
2
1
Выбор схем балочных клеток
2
1.2 Подбор сечения второстепенных и вспомогательных балок 3
2. РАСЧЕТ И КОНСТРУИРОВАНИЕ ГЛАВНОЙ БАЛКИ 4
2.1 Компоновка и подбор сечения главной балки 5
2.2 Изменение сечения балки по длине 8
2.3 Проверка местной устойчивости элементов балки 10
2.4 Расчет поясных швов 16
2.5 Расчет укрупнительного монтажного стыка балки 17
2.6 Расчет опорного узла балки 19
3. РАСЧЕТ И КОНСТРУИРОВАНИЕ ЦЕНТРАЛЬНО-СЖАТЫХ КОЛОНН
3.1 Определение расчетной длины колонны и действующих нагрузок 22
3. 2
Расчет сплошной колонны
22
2
Расчет сплошной колонны
22
3.3 Расчет базы колонны 25
3.4 Расчет оголовка колонны 28
ЛИТЕРАТУРА 30
Как рассчитать или Формула Длина сварки 1
Добавил: wahid nawawi | 17 сентября 2012 г.
Как рассчитать или формула длины сварки 1
Приветствуем наших читателей…..
В этом посте я хочу поделиться знаниями о том, как рассчитать длину сварки. Эта статья может не быть стандартной формулой… которую, очевидно, можно использовать в качестве дополнительной ссылки для ваших расчетов, потому что в некоторых случаях, с которыми я столкнулся, есть некоторые формулы, используемые для определения длины сварки.
Первичный ключ для определения длины сварки; сначала мы должны найти объем работы, который мы будем рассчитывать.
По этому поводу поделюсь опытом расчета длины для типовой сварки следующим образом:
- Угловой шов
- V-образный сварной шов
- L-образный сварной шов
- K-образный сварной шов и
- X-образный сварной шов.
Длина сварки очень полезна – используется в качестве параметра в дополнение к ходу сварки в качестве курса сварки для определения предполагаемого графика, рабочей силы, человеко-часов и т. д.
Давайте обсудим по одному из 5 вышеперечисленных типов сварки.
Прежде чем рассчитать длину сварки для типа сварки угловым швом, сначала мы должны рассчитать рабочий объем для углового шва (пересчет на угловой шов 6 мм).
Формула:
Объем углового сварного шва = ((S² x 1,21)/2) /21,78
Единица измерения объема углового сварного шва: мм
Результат расчета объема углового сварного шва при преобразовании углового шва в 6 мм. После того, как мы найдем рабочий объем (объем углового шва), мы можем определить величину длины сварки углового шва по формуле ниже:
После того, как мы найдем рабочий объем (объем углового шва), мы можем определить величину длины сварки углового шва по формуле ниже:
Формула длины сварного шва Тип углового шва:
= Объем углового шва x длина сварного шва / 1000
или
= (((S² x 1,21)/8 ldght x 9007.7) / 1000
Где:
- S = толщина или размер скругления (мм)
- Объем углового шва (мм)
- Длина сварки (мм)
- Длина углового сварного шва (м)
Примечания:
Приведенный выше расчет только для расчета длины сварки с одинарным угловым швом (1F), если мы использовали двойной угловой шов (2F), мы только умножаем результат длины сварки на 2 (два).
Ниже приведен образец таблицы для преобразования результатов расчета в скругление 6 мм (объем углового сварного шва) для каждого размера скругления.
- Размер скругления 5 мм -> Результат после преобразования скругления 6 мм составляет 0,7 мм
- Размер скругления 6 мм -> Результат после преобразования скругления 6 мм составляет 1,0 мм
- Размер скругления 7 мм -> Результат после преобразования скругления 6 мм составляет 1,4 мм
- Размер скругления 8 мм -> Результат после преобразования скругления 6 мм составляет 1,8 мм
- Размер скругления 9 мм -> Результат после преобразования скругления 6 мм составляет 2,3 мм
- Размер скругления 10 мм -> Результат после преобразования скругления 6 мм составляет 2,8 мм
- Размер скругления 11 мм -> Результат после преобразования скругления 6 мм составляет 3,4 мм
- Размер скругления 12 мм -> Результат после преобразования скругления 6 мм составляет 4,0 мм
- Размер скругления 13 мм -> Результат после преобразования скругления 6 мм составляет 4,7 мм
- Размер скругления 14 мм -> Результат после преобразования скругления 6 мм в 5,4 мм
- и, пожалуйста, продолжайте упражнение
============================================== ==
Дополнительная информация:
Если вы тренируетесь, может быть любой другой результат значения объема углового шва (преобразование углового шва 6мм).
Образец:
Пожалуйста, рассчитайте или переведите в угловой шов 6 мм (объем углового сварного шва) для размера скругления 10 мм.
Ответ:
Объем углового сварного шва = ((S² x 1,21)/2)/21,78
= ((10² x 1,21)/2) /21,78
= 2,77 мм
Таким образом, мы можем использовать объем углового сварного шва 2,8 мм.
============================================== ===
Пример примера:
1. Рассчитайте длину сварки, если размер галтели 16 мм и длина сварки 2600 мм?
Ответ:
Длина сварки 1F =
= Объем углового сварного шва x Длина сварного шва / 1000
= 7,1 x 12000/1000
= 18,5 м
Одиночный угловой шов (1F)
a. Двойной угловой шов (2F)
Ответ:
a. Длина сварки 1F =
= Объем углового шва x Длина сварки / 1000
= 1,8 x 12000/1000
= 21,6 м
a. Длина сварки 2F
Длина сварки 2F
= (Объем углового сварного шва x Длина сварного шва / 1000) x 2
= (1,8 x 12000/1000) x 2
= 43,2 м
Пожалуйста, сообщите, если есть какая-либо ошибка. Спасибо большое….
Нравится:
Нравится Загрузка…
Рубрика: Проектирование, Трубопроводы, ОК/КК, Структура | Теги: Belajar Welding, длина сварки cara menghitung, как рассчитать длину сварки, Rumus Menghitung Длина сварки, наука, сварка, Сварное филе, длина сварки
Проектирование угловых сварных швов для прямоугольных быстрорежущих сталей
Джеффри А. Пэкер
Bahen/Tanenbaum Профессор гражданского строительства, Университет Торонто, Онтарио, Канада
Mindocel Post, Департамент гражданского строительства Sun 9022 Инженерия, Университет Торонто, Онтарио, Канада
Для соединений из быстрорежущей стали, действующих норм, стандартов, спецификаций и руководств по проектированию (Wardenier et al. , 2008; Packer et al., 2009; Packer et al., 2010; ISO, 2013 ) признать два основных принципа проектирования угловых сварных швов: (i) сварной шов может иметь такие пропорции, чтобы он развивал предел текучести соединенного ответвления из быстрорежущей стали; (ii) размер сварного шва может быть таким, чтобы он выдерживал фактические усилия в соединенном ответвлении из быстрорежущей стали.
, 2008; Packer et al., 2009; Packer et al., 2010; ISO, 2013 ) признать два основных принципа проектирования угловых сварных швов: (i) сварной шов может иметь такие пропорции, чтобы он развивал предел текучести соединенного ответвления из быстрорежущей стали; (ii) размер сварного шва может быть таким, чтобы он выдерживал фактические усилия в соединенном ответвлении из быстрорежущей стали.
Метод (i) дает верхний предел требуемого размера сварного шва. Следовательно, это может быть чрезмерно консервативным, когда силы ответвления малы по сравнению с пропускной способностью элемента ответвления. Метод (ii) включает рассмотрение фактической длины группы сварных швов. Как правило, он позволяет «уменьшить размер» сварного шва и, следовательно, популярен. AISC 360 (AISC, 2010) принял Метод (ii) в Разделе K (Таблица K4.1) для сварных соединений с прямоугольными быстрорежущими станками, указав различные эффективные длины сварного шва, l e , для различных типов подключения и ситуаций нагрузки. Подробную информацию об этих двух методах можно найти в более ранней технической статье «Сварка полых структурных секций». В качестве продолжения в этой статье обсуждаются особые соображения по применению глав J и K стандарта AISC 360 к проектированию угловых сварных швов прямоугольных быстрорежущих сталей.
Подробную информацию об этих двух методах можно найти в более ранней технической статье «Сварка полых структурных секций». В качестве продолжения в этой статье обсуждаются особые соображения по применению глав J и K стандарта AISC 360 к проектированию угловых сварных швов прямоугольных быстрорежущих сталей.
Влияние угла нагрузки на прочность углового шва
Пункты о конструкции угловых швов в разделе J2.4(a) AISC 360 разрешают использование так называемого «коэффициента повышения направленной прочности» для угловых швов (т. е. « 1,00 + 0,50sin 1,5 θ” в уравнении J2-5), что позволяет повысить прочность сварного шва, когда направление нагрузки непараллельно оси сварного шва. Принятие коэффициента повышения направленной прочности или «коэффициента sinθ» в AISC 360 было основано на экспериментальных исследованиях соединений внахлестку, где соединение подвергалось нагрузке при сдвиге (Миазга и Кеннеди, 1989; Лесик и Кеннеди, 1990). Установлено, что прочность испытанных угловых швов постепенно увеличивалась в 1,5 раза при увеличении угла нагружения от 0° (шов с продольной нагрузкой) до 9°. 0˚ (сварной шов с поперечной нагрузкой). Однако AISC 360 не разрешает использовать «коэффициент sinθ», когда «метод эффективной длины» AISC 360, глава K, используется для определения пропорций угловых сварных швов в соединениях из быстрорежущей стали (AISC 360, Комментарий к K4) по следующим причинам:
0˚ (сварной шов с поперечной нагрузкой). Однако AISC 360 не разрешает использовать «коэффициент sinθ», когда «метод эффективной длины» AISC 360, глава K, используется для определения пропорций угловых сварных швов в соединениях из быстрорежущей стали (AISC 360, Комментарий к K4) по следующим причинам:
- В отличие от соединений внахлестку, угловые сварные швы во многих соединениях из быстрорежущей стали имеют приварное соединение, нагруженное растяжением или изгибом, а не сдвигом.
- Поскольку сварку можно выполнять только на одной стороне стенки полого профиля, угловые швы на элементах из быстрорежущей стали будут подвержены локальному эксцентриситету. Например, растягивающая нагрузка в прикрепленной стене создаст дополнительное растягивающее напряжение в корне сварного шва (см. рис. 1). На самом деле, нормы и стандарты Северной Америки признают, что внецентренная нагрузка на угловой шов, вызывающая натяжение в корне шва, может снизить пропускную способность сварного шва.
 Например, CSA W59 (CSA, 2013), пункт 4.1.3.3.2, гласит, что … «Одиночный угловой шов и одиночный сварной шов с частичным проваром с разделкой кромок не должны подвергаться изгибу вокруг продольной оси сварного шва, если он вызывает растяжение в корне шва». сварка». В разделе 2.6.2 AWS D1.1 (AWS, 2010) указано, что при расчете сварных соединений расчетные напряжения должны включать напряжения, возникающие из-за эксцентриситета, вызванного совмещением соединяемых деталей, размером и типом сварных швов, хотя в этом разделе относятся к соединениям, которые не являются трубчатыми.
Например, CSA W59 (CSA, 2013), пункт 4.1.3.3.2, гласит, что … «Одиночный угловой шов и одиночный сварной шов с частичным проваром с разделкой кромок не должны подвергаться изгибу вокруг продольной оси сварного шва, если он вызывает растяжение в корне шва». сварка». В разделе 2.6.2 AWS D1.1 (AWS, 2010) указано, что при расчете сварных соединений расчетные напряжения должны включать напряжения, возникающие из-за эксцентриситета, вызванного совмещением соединяемых деталей, размером и типом сварных швов, хотя в этом разделе относятся к соединениям, которые не являются трубчатыми.
- Экспериментально было показано, что включение «коэффициента sinθ» в расчет прочности, как правило, небезопасно при применении к прямоугольным угловым сварным соединениям из быстрорежущей стали и быстрорежущей стали в сочетании с текущим сварным швом главы K AISC 360. эффективная длина/свойства, поскольку целевые уровни структурной надежности не достигаются (Packer and Sun, 2011; McFadden et al.
 , 2013; McFadden and Packer, 2014; Tousignant and Packer, 2014).
, 2013; McFadden and Packer, 2014; Tousignant and Packer, 2014).
Кроме того, согласно недавнему экспериментальному исследованию (Packer et al., 2015) поведения угловых сварных соединений между быстрорежущей сталью и жесткими торцевыми пластинами (см. рис. 2), где эффективной будет вся длина сварного шва (т. «метод эффективной длины» AISC неприменим), путем сравнения экспериментально полученных значений прочности сварного шва с расчетной номинальной прочностью в соответствии с AISC 360 было обнаружено, что:
Рис. 2: Образцы соединения быстрорежущей стали с жесткой пластиной, испытанные Packer et al. (2015)- Расчет прочности, включая коэффициент повышения направленной прочности, приводит к прогнозам, которые не имеют достаточного запаса прочности. Следовательно, необходимо наложить ограничения на применение такого коэффициента повышения направленной прочности для угловых сварных швов в соединениях из быстрорежущей стали, независимо от типа соединения (например, соединение быстрорежущей стали с быстрорежущей сталью или соединение быстрорежущей стали с пластиной).
 Таким образом, номинальное напряжение металла шва следует рассчитывать как F nw = 0,60F EXX по таблице J2.5.
Таким образом, номинальное напряжение металла шва следует рассчитывать как F nw = 0,60F EXX по таблице J2.5. - Если коэффициент повышения направленной прочности не включен в расчет прочности угловых сварных швов из быстрорежущей стали, можно использовать уравнения AISC 360 с достижением адекватного уровня безопасности.
- Как правило, фактическая плоскость излома испытанного сварного шва находится ближе к поверхности сплавления быстрорежущей стали (см. рис. 3) и имеет более длинную линию разрушения. Следовательно, консервативно использовать «эффективную толщину шва» в соответствии с определением AISC 360 (т. е. минимальное расстояние между корнем углового шва и поверхностью треугольного профиля сварного шва) в расчетах прочности.
Взаимодействие между угловыми швами при разных углах нагрузки для группы линейных сварных швов (т. е. все элементы сварных швов расположены на одной линии или параллельны, следовательно, имеют одинаковую деформационную способность под действием приложенной нагрузки), в разделе J2.4(c) приведены положения для концентрически нагруженного соединения с элементами углового сварного шва с несколькими ориентациями. (продольные и поперечные к направлению приложенной нагрузки). В нем указано, что номинальная прочность (R nw ) концентрически нагруженных соединений как с продольными, так и с поперечными угловыми швами, определяется как большее из уравнений J2-10a и J2-10b.
е. все элементы сварных швов расположены на одной линии или параллельны, следовательно, имеют одинаковую деформационную способность под действием приложенной нагрузки), в разделе J2.4(c) приведены положения для концентрически нагруженного соединения с элементами углового сварного шва с несколькими ориентациями. (продольные и поперечные к направлению приложенной нагрузки). В нем указано, что номинальная прочность (R nw ) концентрически нагруженных соединений как с продольными, так и с поперечными угловыми швами, определяется как большее из уравнений J2-10a и J2-10b.
R NW = R NWL +R NWT
(J2-10A)
R NW = 0,85R NWL +1,5.53333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333.. Н.П. , которая учитывает разницу в деформации между продольными и поперечными угловыми швами в группе сварных швов, была разработана на основе испытаний соединений внахлестку с несколькими сегментами сварки с разной ориентацией (Callele et al. , 2009).). В результате несовместимости деформаций поперечный шов препятствует тому, чтобы продольный шов достиг своей полной мощности до того, как произойдет разрушение соединения. Следовательно, испытанные группы сварных швов обладали мощностями, значительно меньшими, чем сумма прочностей отдельных сегментов сварных швов. Каллеле и др. (2009) предложили простой метод консервативного учета этого явления за счет снижения пропускной способности более пластичных сварных швов на 0–15 %. Например, для группы сварных швов, состоящей из продольных и поперечных швов, продольный шов может развить только 85% своей полной мощности до разрушения соединения, что отражено в уравнении J2-10b.
, 2009).). В результате несовместимости деформаций поперечный шов препятствует тому, чтобы продольный шов достиг своей полной мощности до того, как произойдет разрушение соединения. Следовательно, испытанные группы сварных швов обладали мощностями, значительно меньшими, чем сумма прочностей отдельных сегментов сварных швов. Каллеле и др. (2009) предложили простой метод консервативного учета этого явления за счет снижения пропускной способности более пластичных сварных швов на 0–15 %. Например, для группы сварных швов, состоящей из продольных и поперечных швов, продольный шов может развить только 85% своей полной мощности до разрушения соединения, что отражено в уравнении J2-10b.
Обозначение
E = эксцентричность
F EXX = Прочность на заполнители металла
F NW = Номинальное напряжение металла Weld
L E = Эффективная длина WELD
P = Applied Ciple. = номинальная прочность сварного соединения
R nwl = суммарная номинальная прочность продольно нагруженных угловых швов
R NWT = общая номинальная прочность сварных швов с поперечной нагрузкой (без применения «sin θ»)
T = толщина стенки ветви RHS
T P = толщина средней тарелки
T W = Эффективная толщина горла. сварного шва
сварного шва
θ = угол нагрузки, измеренный от продольной оси сварного шва, для расчета прочности углового шва (в градусах)
Литература
АИСЦ. 2010. «Технические условия для зданий из конструкционной стали», ANSI/AISC 360-10, Американский институт стальных конструкций, Чикаго, Иллинойс, США.
АМС. 2010. «Нормы и правила сварки конструкций – сталь, 22-е издание», ANSI/AWS D1.1/D1.1M:2010, Американское общество сварщиков, Майами, Флорида, США.
Калле, Л.Дж., Драйвер, Р.Г. и Грондин, Г.Ю. 2009. «Конструкция и поведение многоориентационных соединений угловым сварным швом», AISC Engineering Journal, Vol. 46, № 4, стр. 257-272.
CSA. 2013. «Сварная стальная конструкция (дуговая сварка металлом)», CSA W59-13, Канадская ассоциация стандартов, Торонто, Канада.
ИСО. 2013. «Процедура статического расчета сварных соединений полых профилей – рекомендации», ISO 14346:2013 (E), Международная организация по стандартизации, Женева, Швейцария.
Лесик, Д. Ф. и Кеннеди, Д. Дж. 1990. «Предельная прочность угловых сварных соединений, загруженных в плоскости», Канадский журнал гражданского строительства, Vol. 17, № 1, стр. 55-67.
Макфадден, М. Р., Сан, М. и Пакер, Дж. А. 2013. «Проектирование и изготовление сварных швов для RHS-соединений», Steel Construction – Design and Research, Vol. 6, № 1, с. 5-10.
Макфадден, М. Р. и Пакер, Дж. А. 2014. «Эффективные свойства сварного шва для полых структурных секций Т-образных соединений при плоскостном изгибе ветвей», AISC Engineering Journal, Vol. 51, № 4, стр. 247-266.
Миазга, Г. С. и Кеннеди, Д. Дж. 1989. «Поведение угловых сварных швов в зависимости от угла нагрузки», Канадский журнал гражданского строительства, Vol. 16, № 4, с. 583-599.
Пакер Дж.А., Варденье Дж., Чжао С.-Л., ван дер Вегте Г.Дж. и Куробане, Ю. 2009 г. «Руководство по проектированию соединений прямоугольного полого сечения (ПСП) при преимущественно статической нагрузке», Руководство по проектированию CIDECT № 3, 2-е издание, Международный комитет по развитию и исследованию труб, Женева, Швейцария.
Пакер, Дж. А., Шерман, Д. и Лечче, М. 2010. «Соединения полых структурных секций», Руководство по проектированию стали № 24, Американский институт стальных конструкций, Чикаго, Иллинойс, США.
Пакер, Дж. А. и Сан, М. 2011. «Проектирование сварных швов для прямоугольных соединений из быстрорежущей стали». Инженерный журнал AISC, Vol. 48, № 1, стр. 31-48.
Пакер, Дж. А., Сан, М., Оутвей, П. и Фратер, Г. С. 2015. «Экспериментальная оценка увеличения направленной прочности угловых сварных швов к прямоугольным полым сечениям», 15-й Международный симпозиум по трубчатым конструкциям, Рио-де-Жанейро. , Бразилия, 8 стр.
Тузигант, К. и Пакер, Дж. А. 2014. «Проектирование сварных швов для прямоугольных соединений быстрорежущей стали с перекрытием К-образных соединений», Фаза 2 Отчет для Американского института стальных конструкций, Университет Торонто, Торонто, Канада.
Варденье Дж., Куробане Ю., Пакер Дж. А., ван дер Вегте Г. Дж. и Чжао С. Л. 2008 г. «Руководство по проектированию соединений круглого полого сечения (CHS) при преимущественно статической нагрузке». Руководство по проектированию № 1, 2-е издание, Международный комитет по развитию и исследованию строительных труб, Женева, Швейцария.
А., ван дер Вегте Г. Дж. и Чжао С. Л. 2008 г. «Руководство по проектированию соединений круглого полого сечения (CHS) при преимущественно статической нагрузке». Руководство по проектированию № 1, 2-е издание, Международный комитет по развитию и исследованию строительных труб, Женева, Швейцария.
Июнь 2015 г.
Скачать PDF
Расчет сварного соединения стержня, растянутого под двумя углами, с косынкой
Задача: Проверить режим расчета сварных соединений.
Задание: Проверить угловое сварное соединение растянутого стержня из двух уголков 75х8 с фасонкой.
Каталожные номера: Стальные конструкции. В 3 т. — Т. 1. Элементы стальных конструкций/ Горев В.В., Уваров Б.Ю., Филиппов В.В. и др. — М.: Высшая школа, 2004. с. 159-160.
Соответствие кодам: СНиП II-23-81*, СП 16.13330.2011, СП 16.13330.2017, ДБН Б.2.6-163:2010, ДБН Б. 2.6-198:2014.
2.6-198:2014.
Исходные данные:
| t = 10 мм | толщина косынки |
| Н = 425 кН | Продольная сила |
| R и = 380 МПа | Сталь С245 |
| R wf = 220 МПа | Сварка полуавтоматом СО2 проволокой Св-08Г2С d = 1,2 мм |
| k f1 = 6 мм | Приварной шов на соединенной ножке |
| к f2 = 6 мм | Приварка на свободном участке |
| Раздел | Уголок 75х8 мм |
| Д Ш1 = 175 мм | длина сварного шва вдоль свободного участка |
| l w2 = 80 мм | длина сварного шва вдоль присоединяемого участка |
Файл исходных данных:
Исходные данные КРИСТАЛЛ:
Сталь: C245
1 | |
Сервис-фактор | 1 |
Группа конструкций по таблице 50* СНиП II-23-81* | 1 |
Свойства сварочных материалов: | |
|---|---|
Нормативное сопротивление металла шва по пределу прочности, R wun | 490 Н/мм 2 |
Расчетное сопротивление угловых швов сдвигу металла шва, R wf | 215 Н/мм 2 |
Тип сварки | Автоматы и полуавтоматы, диаметр электродной проволоки не менее 1,4-2,0 мм |
Положение сварного шва | Квартира |
Климатический район | с температурой t > -40°C |
Тип: | Параметры: |
|---|---|
Профиль — Полный ассортимент профилей ГОСТ. | Приварной шов на свободном участке = 6 мм
|
Внутренние силы:
Н = 425 кН
Проверено по СНиП | Чек | Коэффициент использования |
|---|---|---|
Раздел 11.2 Формула (120) | металла шва | 1,018 |
Раздел 11.2 Формула (121) | металла бордюра сплавленного | 0,921 |
Сравнение решений:
Чек | металла шва по пятке |
Источник | 7,9 см / 8 см = 0,9875 |
КРИСТАЛЛ | 1 018 |
Отклонение, % | 3,0 |
Уточненный ручной расчет (см. | 0,7133×425 / (2×0,7×0,6×16,5см×21,50)=1,017 |
Отклонение, % | 0,1 |
Комментарии
Различие в результатах обусловлено различием принятых значений расчетного сопротивления R wf = 220 МПа (книга) и R wf = 215 МПа (проектные нормы и КРИСТАЛЛ ). При этом распределение внешней продольной силы между швами по носке и пятке уголка в проверочном примере точно не указано, т.е. продольная сила в сварном шве по пятке дана как 70% внешней продольной силы, и то, что вдоль пальца ноги, дается как 30% силы. Точное значение продольной силы, действующей в сварных швах по пятке, рассчитывается как:
( B Угол — Y 0 )/ B Угол × N = 0,713333333333333333333333330 гг. y 0 – длина перпендикуляра, опущенного из центра масс угла на соответствующую наружную грань полки.
Как определить размер углового сварного шва с помощью анализа методом конечных элементов (МКЭ)
В предыдущем блоге « Моделирование сварных швов для анализа методом конечных элементов (МКЭ) (добавьте ссылку на этот блог перед публикацией) «. Мы обсудили методы прогнозирования напряжения вокруг углового сварного шва. В этом посте мы хотим представить оптимизированный процесс анализа сварных швов с использованием FEA (в частности, ANSYS Workbench) в качестве основного инструмента. Мы сосредоточимся на том, как правильно определить размер угловых сварных швов, навык, который оказался особенно полезным для сложных сварных соединений.
Метод 1 (более традиционный подход) Прежде чем обсуждать использование МКЭ для определения размеров сварных швов, давайте сначала рассмотрим традиционный подход к определению размеров сварного шва, как описано в разделе «Определение нагрузок при сварке и требований к раструбу с использованием анализа методом конечных элементов с помощью Shell». Модели элементов — сравнение с классическим анализом» М. А. Уивера.
Модели элементов — сравнение с классическим анализом» М. А. Уивера.
Пример использования Метода 1:
Простое Т-образное соединение, изготовленное из листов ASTM A36 толщиной 3/8″, должно быть сварено с двух сторон угловым швом. Основная пластина закреплена в отверстиях болтов, и на нагрузке [-200, -2000, 3000] LBF применяется в отверстии, как показано ниже:
Недостатки метода 1:
Хотя подход с использованием метода 1 для расчета размера сварного шва может быть эффективным методом, он не всегда практичен. Учтите следующие недостатки :
- Это может занять некоторое время, особенно в случае более сложных сварных соединений, чем в предыдущем примере.
- Предполагается, что внешние силы равномерно распределены по сварному шву. Это не соответствует действительности и может быть опасным предположением.

- Для сложных сварных швов и форм метод 1 нельзя использовать без упрощения анализа.
Программы FEA могут использоваться как более точный способ прогнозирования нагрузок на сварной шов. Смоделировав случай нагрузки с помощью FEA, мы можем использовать ANSYS, чтобы сообщить нам, какие нагрузки и моменты находятся в области, характерной для интересующего сварного шва.
Пример использования метода 2:
Рассмотрим тот же сценарий загрузки, что и в примере 1:
- С помощью ANSYS Workbench мы преобразуем модель в оболочку.
- Размер сетки. Для этой конкретной модели мы хотим, чтобы размер сетки составлял определенную часть длины сварного шва. Наша длина сварного шва составляет 4 дюйма, поэтому размер сетки 0,1 даст 40 точных элементов поперек сварного шва. Это будет важно позже.

- Добавьте смещение линии разделения от края сварного шва. Эта линия разделения будет определять область, из которой будут вытягиваться силы и моменты. Смещение от края гарантирует, что узлы находятся внутри сварного шва и не являются общими для нескольких тел.
- Перед запуском моделирования необходимо включить «Узловые силы». Доступ к этому параметру осуществляется через «Настройки анализа/Управление выводом» на боковой панели (как показано):
- Перед запуском симуляций мы хотим настроить 3-кратные «определяемые пользователем» результаты из параметров ENFOZ, ENFOY и ENMOY. Эти параметры дают узловые равнодействующие силы и моменты в направлении выбранной оси.
- Чтобы получить доступ к этим пользовательским результатам, щелкните «Решения/Рабочий лист» и прокрутите вниз до нужных параметров (указанных выше).
- Щелкните правой кнопкой мыши 3 параметра и выберите «Создать пользовательский результат».

- Последний шаг — ограничить эти пользовательские результаты созданным нами путем. Это можно сделать одновременно со всеми тремя пользовательскими результатами, выделив все три и изменив «Метод определения области» на «Путь» и выбрав предопределенный путь (сварной шов).
- Ниже приведены результаты для ENFOZ, которые представляют собой равнодействующие силы в каждом узле в направлении Z поперек траектории сварного шва.
- Кроме того, данные можно просмотреть в разделе «Табличные данные», а затем скопировать и вставить на лист Excel.
Расчетные значения проверки работоспособности:
В качестве двойной проверки правильности вытягивания значений ANSYS сумма результатов должна СООТВЕТСТВОВАТЬ первоначально приложенным нагрузкам ( Примечание: суммы могут не точно соответствовать первоначальным нагрузкам из-за ошибок округления ):
- Приблизительно 3000 фунтов силы в направлении Z
- Приблизительно 2000 фунтов силы в направлении Y
- 200 фунтов силы * 4,25 дюйма = примерно 850 фунтов силы на дюйм относительно оси Y
(d = 4,00 дюйма)
Уравнение, предложенное Уивером для расчета размера раструба сварного шва:
Примечание. Чтобы изменить формат, чтобы он соответствовал нашему листу Excel, мы делим каждое значение на длину каждого элемента (0,1 дюйма).
Чтобы изменить формат, чтобы он соответствовал нашему листу Excel, мы делим каждое значение на длину каждого элемента (0,1 дюйма).
Графики М-результатов:
На М-графике мы видим равномерно распределенный момент по сварному шву.
Поскольку значения среднего и максимального моментов довольно близки, мы будем осторожны и используем для расчета максимальное значение 217 фунт-сила-дюйм/дюйм.
Графики результатов P:
Для P мы можем видеть ценность использования FEA для определения распределенной силы через сварной шов.
Мы видим, что по всей длине сварного шва существует большой диапазон тягового усилия. В расчетах предлагается использовать максимальное абсолютное значение P, -4603 фунт-сила/дюйм.
Графики результатов V:
Для графика V мы видим менее экстремальное распределение силы, но все же некоторое результирующее изменение:
Аналитик может использовать для расчета среднее или максимальное значение V.
Здесь, поскольку сила распределяется достаточно равномерно, за исключением двух конечных узлов, мы будем использовать среднее значение V, равное 435 фунт-сила/дюйм.
Расчет размера сварного шва:
Подставив значения P, V и M в уравнение Уивера, мы можем рассчитать размер горловины 0,161 дюйма и размер углового участка 0,227 дюйма 9.0009
Это значение примерно на 10 % меньше, чем традиционное вычисление длины ноги, равное 0,26 дюйма, и его следует считать более точным, поскольку при расчете использовались более точные значения силы.
Заключение В то время как два метода, показанные выше, дали сопоставимые результаты, реальная ценность метода 2 заключается в использовании для определения размеров сварных швов в более сложных сварных соединениях, таких как сварные соединения с использованием нескольких пластин различной формы и толщины. Для сложных сварных соединений Метод 1 может занять очень много времени. Использование FEA для определения критических зон сварки и извлечения связанных сил и моментов ( , метод 2 ) может помочь оптимизировать процесс определения размеров сварного шва и предоставить более точные результаты.
Использование FEA для определения критических зон сварки и извлечения связанных сил и моментов ( , метод 2 ) может помочь оптимизировать процесс определения размеров сварного шва и предоставить более точные результаты.
Длина сварного шва в пересчете на площадь параллельного углового шва Расчет
0009 | AcreAcre (US Survey)AreArpentBarnCarreauCircular InchCircular MilCuerdaDecareDunamElectron Cross SectionHectareHomesteadMile (Roman)²Mile (Statute)²MuPingPlazaPyongRoodSabinSectionSquare AngstromSquare CentimeterSquare ChainSquare DecameterSquare DecimeterSquare FootSquare Foot (US Survey)Square HectometerSquare InchSquare KilometerSquare MeterSquare MicrometerSquare MilSquare MileSquare Mile (US Survey)Square MillimeterSquare NanometerSquare ОкуньКвадратный столбКвадратный стерженьКвадратный стержень (исследование США)Квадратный дворСтреммаГородВарас Кастелланас КуадВарас Конукерас Куад | +10% -10% | |
✖Толщина листа – это состояние или качество толщины. | A.U. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% |
✖Длина сварного шва представляет собой линейное расстояние каждого сегмента сварного шва. | А.У. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Длина сварного шва по площади параллельного углового шва Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовую единицу
Площадь слоя сварного шва: 0,4 квадратных метра —> 0,4 квадратных метра Преобразование не требуется
Толщина листа: 12 миллиметров —> 0,012 Метр (Проверьте преобразование здесь)
ШАГ 2: Расчет формулы
ШАГ 3: Преобразование результата в единицу измерения
23,5737859500236 Метр —> Преобразование не требуется
< 9 Калькуляторы длины сварного шваДлина шва по площади параллельного углового шва Формула
Длина сварного шва = площадь сварного шва/(1,414*толщина листа)
л = А/(1,414*t)
Что такое предел прочности на примере?
Прочность на растяжение — это измерение силы, необходимой для того, чтобы натянуть что-то, например, веревку, проволоку или конструкционную балку, до точки, где она порвется. Прочность материала на растяжение — это максимальное растягивающее напряжение, которое он может выдержать до разрушения, например, разрыва.
Прочность материала на растяжение — это максимальное растягивающее напряжение, которое он может выдержать до разрушения, например, разрыва.
Как рассчитать длину шва по площади параллельного углового шва?
Длина сварного шва в пересчете на площадь параллельного углового шва Калькулятор использует Длина сварного шва = Площадь слоя сварного шва/(1,414*Толщина листа) для расчета длины сварного шва, Формула длины сварного шва в пересчете на площадь параллельного углового шва определяется как линейное расстояние каждого сегмента сварного шва. Длина сварного шва обозначается l 9символ 0870.
Как рассчитать длину шва по площади параллельного углового шва с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для длины сварного шва в пересчете на площадь параллельного углового шва, введите площадь сварного шва (A) и толщину пластины (t) и нажмите кнопку расчета. Вот как можно объяснить расчет длины сварного шва с точки зрения площади параллельного углового шва с заданными входными значениями -> 23,57379 = 0,4/(1,414*0,012) .
Вот как можно объяснить расчет длины сварного шва с точки зрения площади параллельного углового шва с заданными входными значениями -> 23,57379 = 0,4/(1,414*0,012) .
Часто задаваемые вопросы
Что такое длина сварного шва в пересчете на площадь параллельного углового шва?
Длина сварного шва по формуле площади параллельного углового шва определяется как линейное расстояние каждого сегмента сварного шва и представляется как l = A/(1,414*t) или Длина сварного шва = площадь сварного шва/ (1,414*Толщина листа) . Площадь сварного шва — это область, подготовленная путем соединения двух металлов для сварки. Толщина листа — это состояние или качество толщины. Мера наименьшего размера твердой фигуры: доска двухдюймовой толщины.
Как рассчитать длину шва по площади параллельного углового шва?
Длина сварного шва по формуле площади параллельного углового шва определяется как линейное расстояние каждого сегмента сварного шва, рассчитанное с использованием Длина сварного шва = Площадь слоя сварного шва/(1,414*Толщина листа) . Чтобы рассчитать длину сварного шва с точки зрения площади параллельного углового шва, вам потребуется площадь сварного шва (A) и толщина пластины (t) . С помощью нашего инструмента вам нужно ввести соответствующее значение площади сварочного слоя и толщины листа и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Чтобы рассчитать длину сварного шва с точки зрения площади параллельного углового шва, вам потребуется площадь сварного шва (A) и толщина пластины (t) . С помощью нашего инструмента вам нужно ввести соответствующее значение площади сварочного слоя и толщины листа и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов расчета длины сварного шва?
В этой формуле длина сварного шва использует площадь сварного шва и толщину листа. Мы можем использовать 8 других способов, чтобы вычислить то же самое, которые следующие:
- Длина сварного шва = площадь сварного шва/(2*толщина шва)
- Длина шва = площадь сварного шва/толщина шва
- Длина сварного шва = площадь слоя сварного шва/(1,414*толщина листа)
- Длина сварного шва = площадь слоя сварного шва/(0,707*толщина листа)
- Длина сварного шва = Площадь сварного шва/(2*Толщина шва)
- Длина сварного шва = Сила/(Растягивающее напряжение*Глубина сварного шва)
- Длина сварного шва = Прочность на растяжение/(1,414*Растягивающее напряжение*Толщина листа) )
- Длина сварного шва = Прочность на растяжение/(0,707*Растягивающее напряжение*Толщина листа)
Доля
Скопировано!
8-A Решенная задача 4-2 для коэффициента запаздывания сдвига U.
 Краткое содержание видео.
Краткое содержание видео. Начнем рассмотрение решенного примера-4-2 Продолжим вместе с коэффициентом запаздывания сдвига, как его оценить? мы собираемся взглянуть на решенную проблему-4-2, от Аби Агайра, из практического подхода к конструкционной стали, решенная проблема касается сварного шва, для одной стороны угла, Это часть видео , который имеет подзаголовок и закрытый заголовок на английском языке.
Civil 120-82- Решенная проблема для сдвиговой задержки, но с использованием сварки-F E Exam Review-Arabic.
Посмотреть это видео на YouTube
Вы можете щелкнуть любое изображение, чтобы увеличить его, затем нажать маленькую стрелку, чтобы просмотреть все остальные изображения в виде слайд-шоу.
Продолжаем вместе с коэффициентом запаздывания сдвига, как его оценить?
Мы рассмотрим решенную задачу-4-2, от Аби Агайра, из версии-3 конструкции из конструкционной стали, решенная задача касается сварного шва, для одной стороны уголка.
На следующем слайде сначала рассмотрим соответствующие уравнения
Существует два способа оценки номинальной прочности элемента, работающего на растяжение, путем получения соответствующих параметров, и второй способ оценки разрыва при растяжении, а также соответствующих параметров.
Марка стали и соответствующие значения Fy, Fult для A36, fy=36 тысяч фунтов/кв. дюйм, fult=58-80 тысяч фунтов/кв.дюйм, марка A572, fy=50 тысяч фунтов/кв.дюйм, марка A572, значение предела прочности=65 тысяч фунтов/кв. дюйм
Это таблицы в соответствии с последней редакцией AISC-360-16, которые мы используем для оценки значений коэффициента запаздывания при сдвиге. В первой таблице для пластин объяснялись три случая пластин.
Случай № 3 — это случай любого растянутого элемента, приваренного к другому элементу поперечным сварным швом, для которого значение U = 1,00.
Случай № 4, в данном случае пластина, уголок, С-образный швеллер и уголок, которые приварены в продольном направлении только на растяжение к другому элементу, для которого значение U определяется уравнением для оценки значения U.
Это различные прямоугольные корпуса, соединенные с одной пластиной или двумя пластинами, и соответствующее значение для каждого случая.
Часть таблицы запаздывания при сдвиге -4- основана на последней спецификации, принятой профессором Аби Агайром .
Это другие случаи из 7 и 8 и соответствующее значение U.
На стр. 53 из книги проф. Сегуи , если у вас есть натяжной элемент, который приварен к одной стойке с пластиной в вертикальном направлении, как показано, а также приварен к продольным верхним и нижним кромкам для другой полки с одинаковым расстоянием сварки верхней и нижней частей или с разными расстояниями верхней и нижней сторон, для которых L1 — длина сварного шва верхней части полки с пластиной, а L 2 — длина сварного шва для нижняя часть ноги.
Верхнее плечо не действует, оно только приварено, но, как и прежде в случае с болтом, это плечо не используется на растяжение вместо умножения площади сетки, как в случае с болтами, на этот раз с помощью сварки , в расчете не будет вычета площади, а брутто будет использоваться.
Значение разрыва при растяжении Pn=Ae*Fult=Ag*U*Fult будет соответственно увеличено.
Из комментария 16-1, стр. 303, для сварного соединения L — длина сварного шва, параллельного линии действия силы, и здесь, как показано, различные длины сварного шва в направлении действия силы.
На рис. CD-3.4 для продольных и продольных плюс поперечных швов L — длина, параллельная силе. В случае разной длины используйте среднюю длину, которая сейчас является нашей заботой для следующей решаемой задачи 4-2 для поперечной задержки.
Решенная задача 4-2 для коэффициента запаздывания сдвига U более подробно.
Если перейти к нашей решенной задаче 4-2 для поперечной задержки, оцените значение U для сварного соединительного уголка L 5x5x3/8, сваренного с трех сторон.
Длина нижнего сварного шва составляет 4 дюйма, длина сварного шва верхней части составляет 6 дюймов, длина сварного шва равна высоте угла. верхняя нога не соединена с задней пластиной.


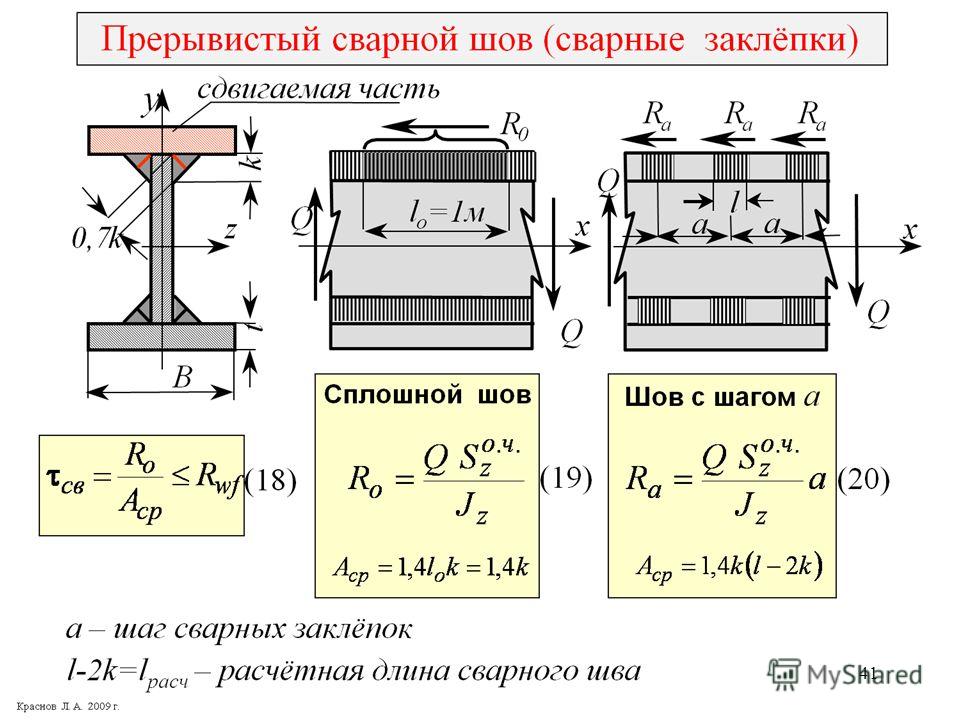 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 Высоты катетов швов по перу уголка и по обушку могут назначаться одинаковыми с учетом требований п.12.8 СНиП II-23-81*. Расчетная длина углового сварного шва принимается не менее 4kfине менее 40 мм.
Высоты катетов швов по перу уголка и по обушку могут назначаться одинаковыми с учетом требований п.12.8 СНиП II-23-81*. Расчетная длина углового сварного шва принимается не менее 4kfине менее 40 мм. Коэффициент условия работы γс= 0,95 (рис. 4).
Коэффициент условия работы γс= 0,95 (рис. 4).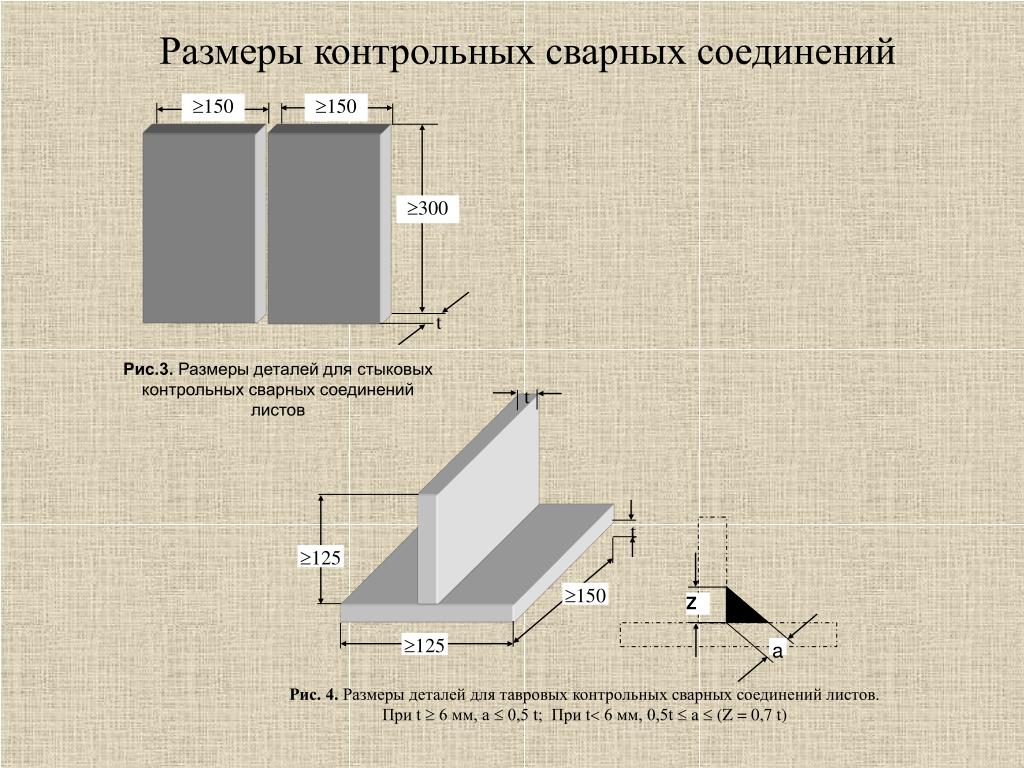
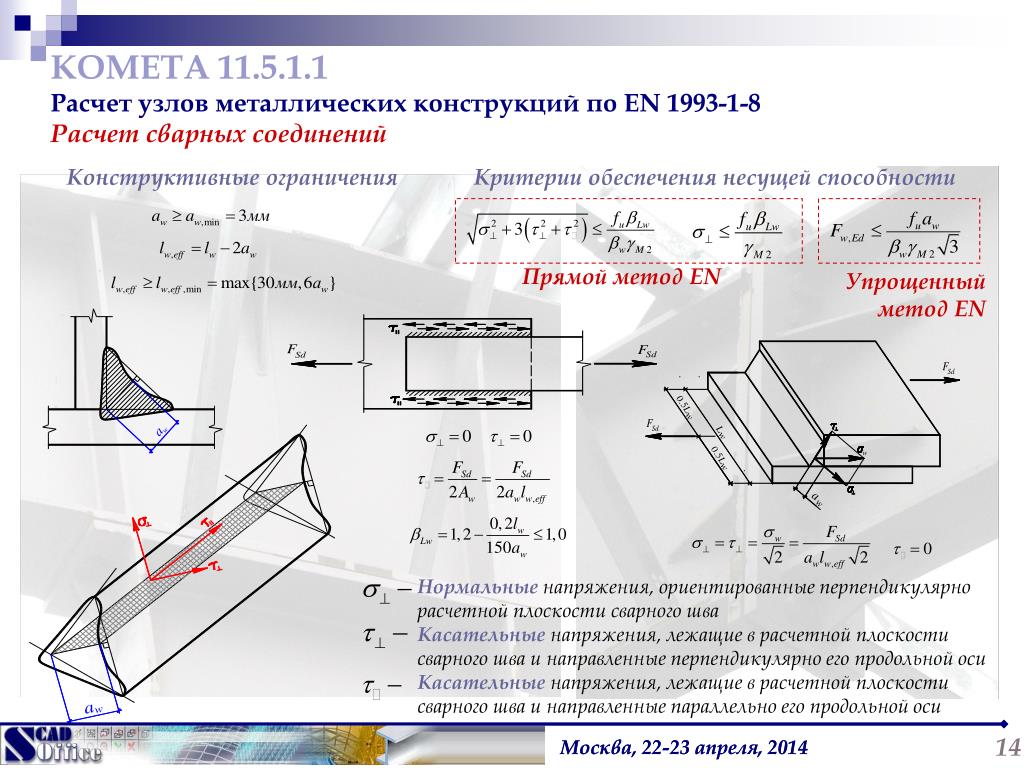 5).
5). е. подобрать сечение растянутого и сжатого сечения стержня стальной фермы.
е. подобрать сечение растянутого и сжатого сечения стержня стальной фермы.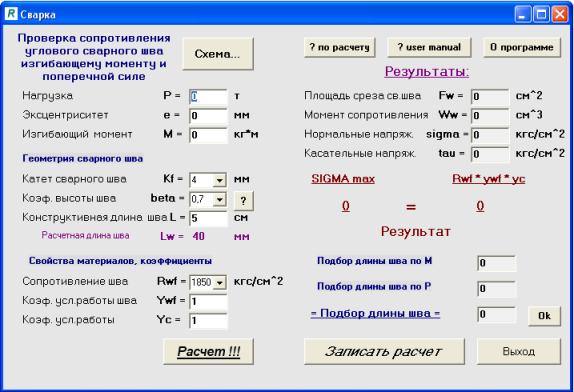 Расчет по прочности производится только в случае наличия ослаблений в расчетном сечении стержней. Если ослаблений нет, то наибольшие по величине напряжения получаются при расчетах устойчивости.
Расчет по прочности производится только в случае наличия ослаблений в расчетном сечении стержней. Если ослаблений нет, то наибольшие по величине напряжения получаются при расчетах устойчивости.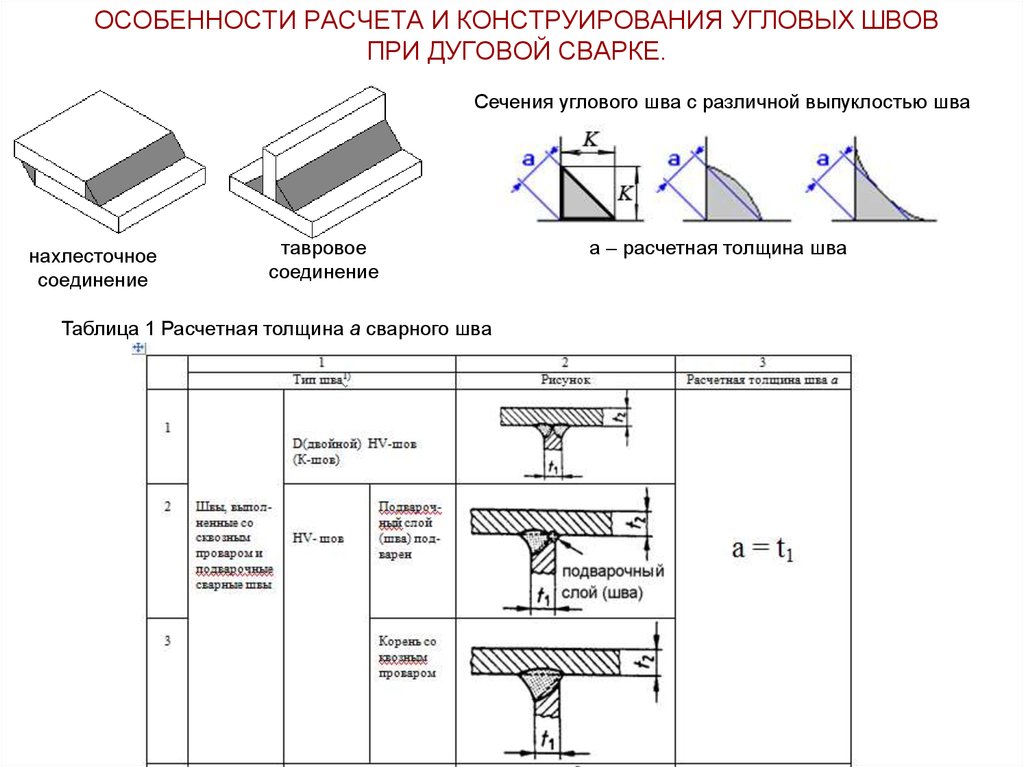 50* СНиП II-23-81*), принимаем из рекомендованных сталей сталь С245.
50* СНиП II-23-81*), принимаем из рекомендованных сталей сталь С245.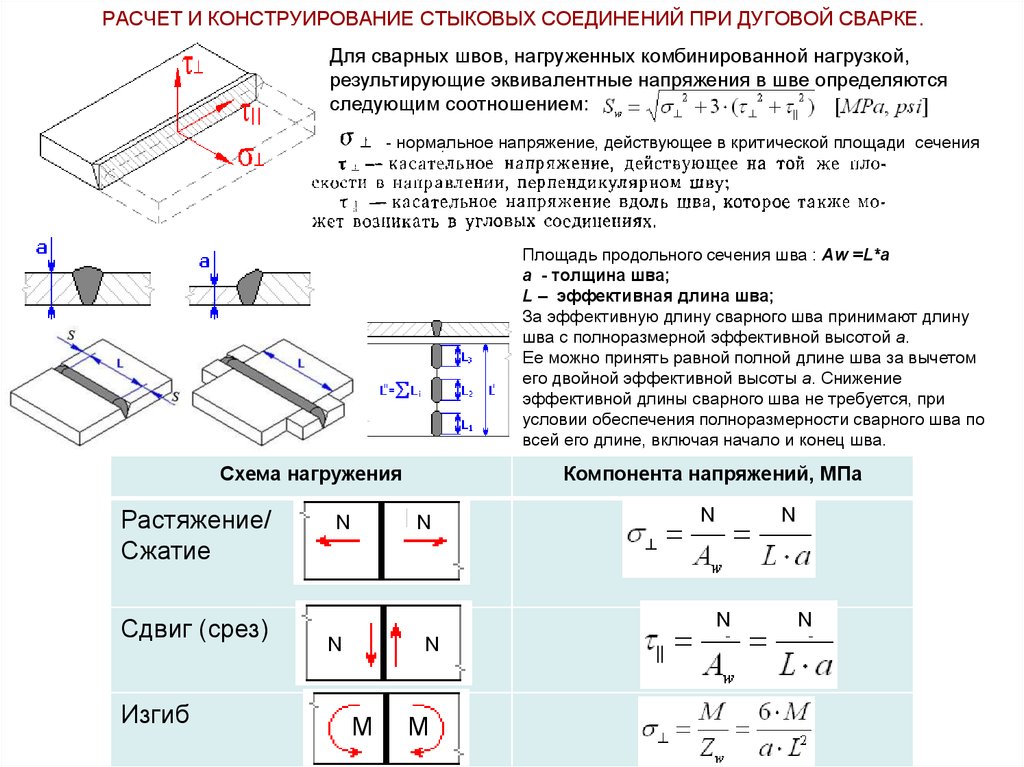
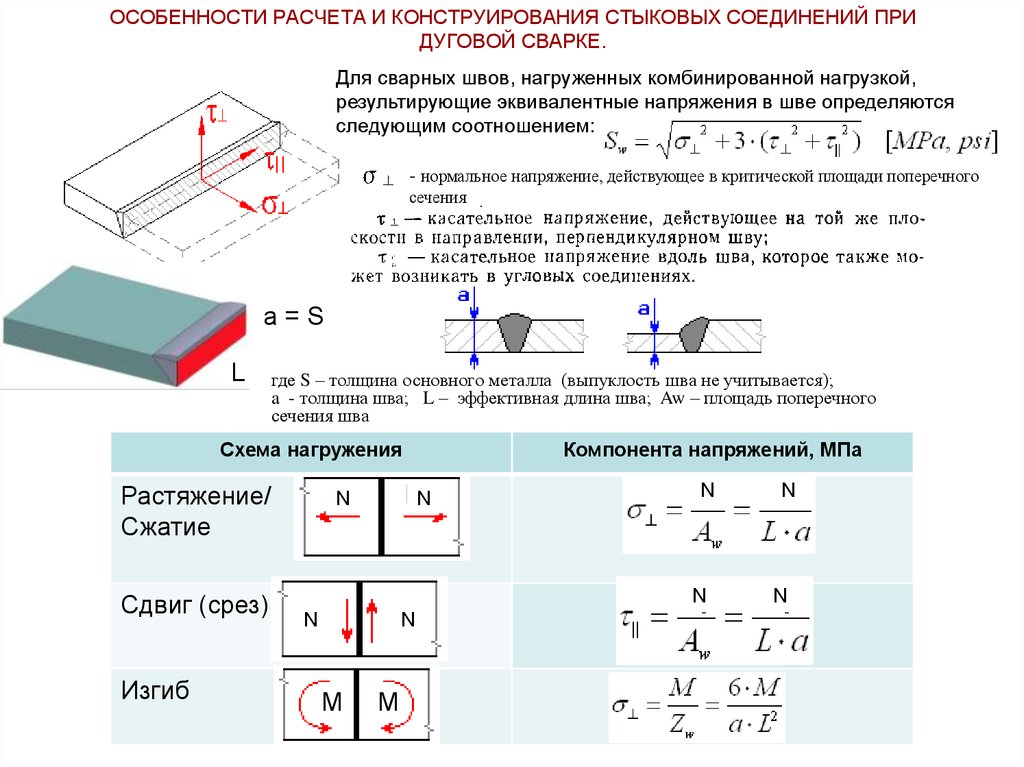 2.2).
2.2).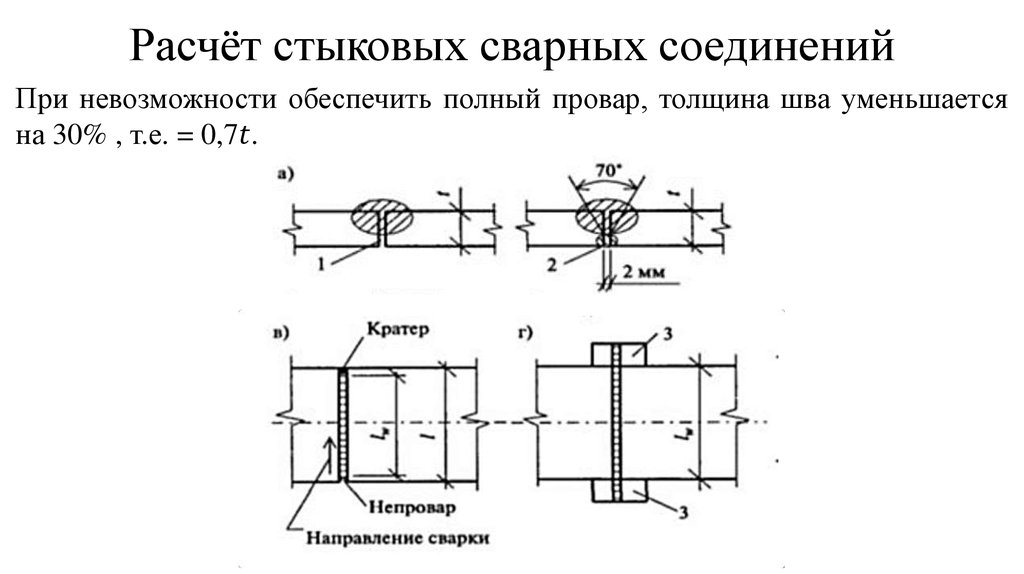 2) подбираем уголки по трем параметрам: A, ix, iy1; при подборе уголков не забываем, что площадь стержня состоит из двух уголков; требуемая площадь одного уголка А1y= 27,17/2 = 13,59 см2; принимаем уголки: 2 уголка 100 x 8; А1y = 15,6 см2; ix,= 3,07 см; iy1= 4,47 см (принятое сечение имеет площадь больше требуемой, а радиусы инерции имеют значения меньше, но близкие к требуемым).
2) подбираем уголки по трем параметрам: A, ix, iy1; при подборе уголков не забываем, что площадь стержня состоит из двух уголков; требуемая площадь одного уголка А1y= 27,17/2 = 13,59 см2; принимаем уголки: 2 уголка 100 x 8; А1y = 15,6 см2; ix,= 3,07 см; iy1= 4,47 см (принятое сечение имеет площадь больше требуемой, а радиусы инерции имеют значения меньше, но близкие к требуемым).
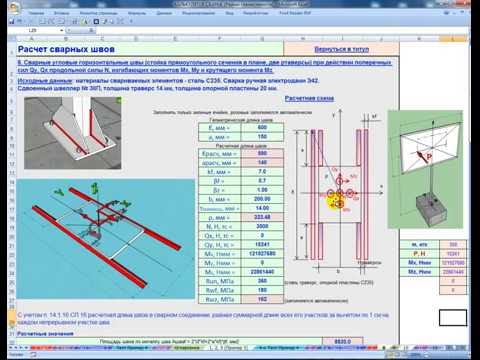
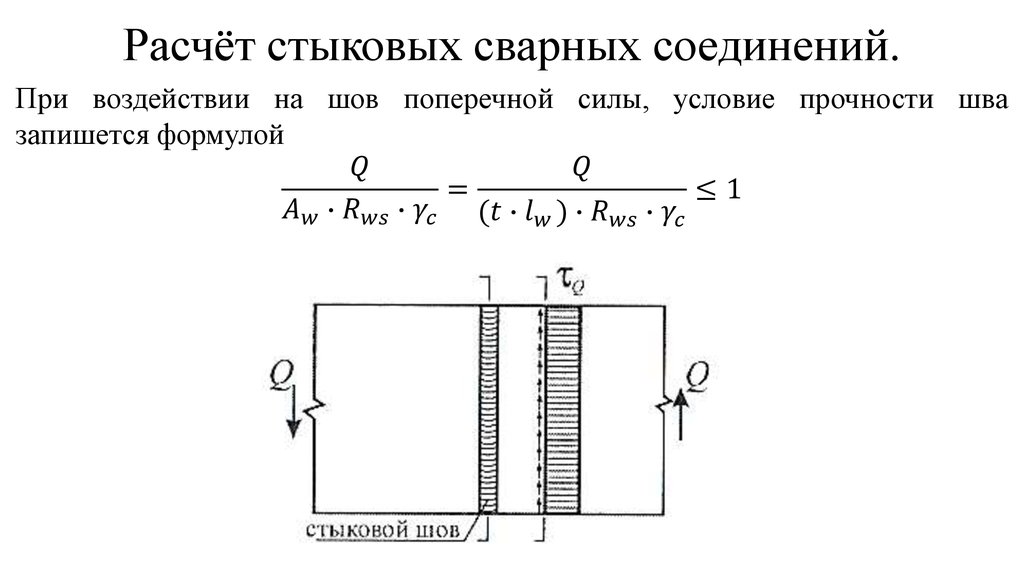 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.029 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.029 с.) Сварные швы часто заменяются абсолютно жёсткими телами, соединяющими детали или же просто объединением перемещений. И в первом, и во втором случае реальная жёсткость сварного шва не учитывается. Наиболее точным способом будет моделирование сварки при помощи объёмных или плоских конечных элементов, однако в случае нестандартных узлов это может вызвать определённые трудности при построении сетки конечных элементов.
Сварные швы часто заменяются абсолютно жёсткими телами, соединяющими детали или же просто объединением перемещений. И в первом, и во втором случае реальная жёсткость сварного шва не учитывается. Наиболее точным способом будет моделирование сварки при помощи объёмных или плоских конечных элементов, однако в случае нестандартных узлов это может вызвать определённые трудности при построении сетки конечных элементов.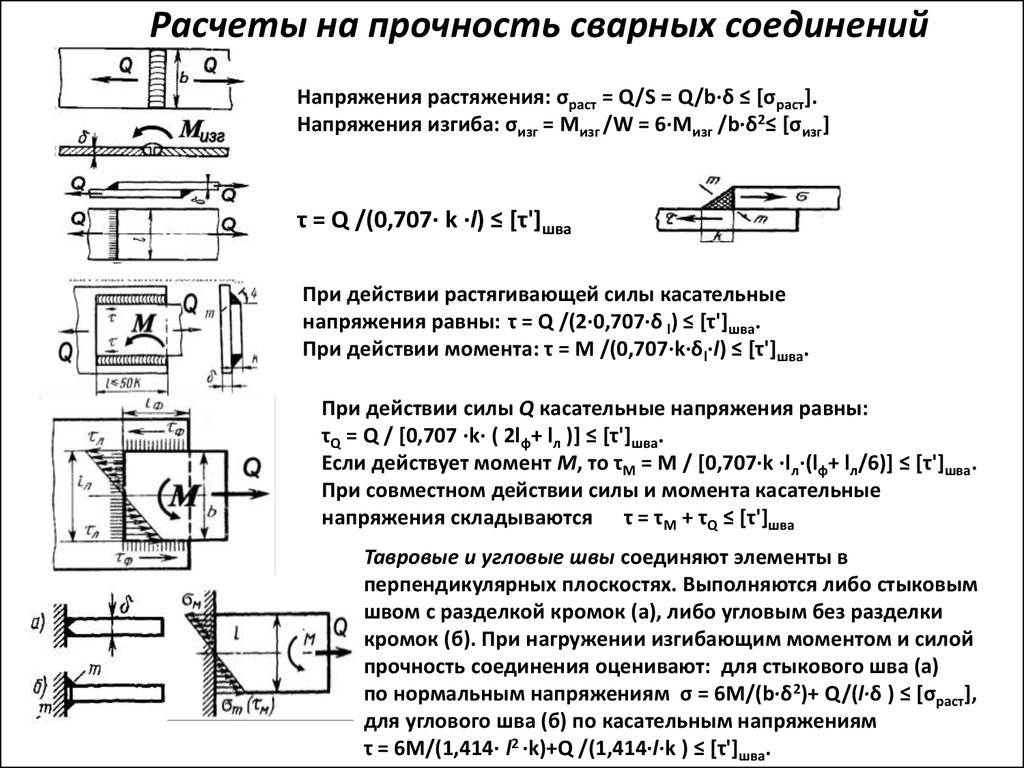 Хотя именно в них зачастую развиваются пластические деформации. Если сварные швы задавать объёмными элементами, то для оценки несущей способности шва придётся анализировать большое количество данных – величины нормальных и касательных напряжений в каждом конечном элементе.
Хотя именно в них зачастую развиваются пластические деформации. Если сварные швы задавать объёмными элементами, то для оценки несущей способности шва придётся анализировать большое количество данных – величины нормальных и касательных напряжений в каждом конечном элементе.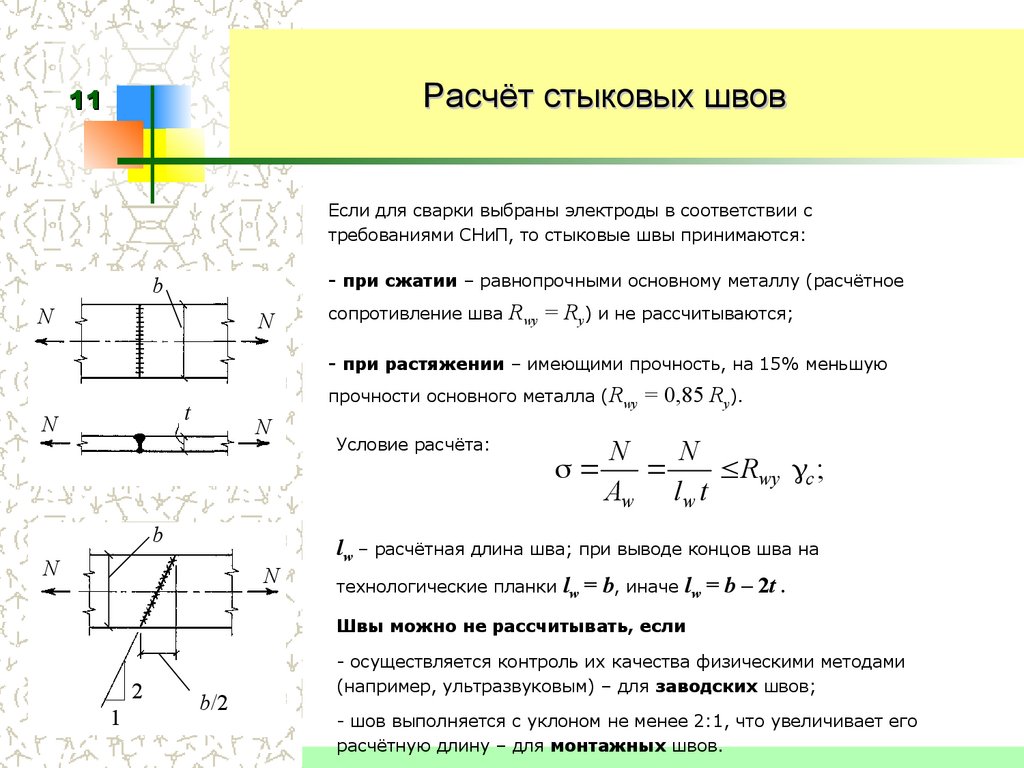 В IDEA StatiCa для стали используется диаграмма Прандтля с небольшим наклоном вверх ветви, отвечающей за текучесть (показана серым цветом на рисунке 3-1). Критерий наступления предельного состояния связывается с достижением главной продольной деформации максимальной величины.
В IDEA StatiCa для стали используется диаграмма Прандтля с небольшим наклоном вверх ветви, отвечающей за текучесть (показана серым цветом на рисунке 3-1). Критерий наступления предельного состояния связывается с достижением главной продольной деформации максимальной величины.
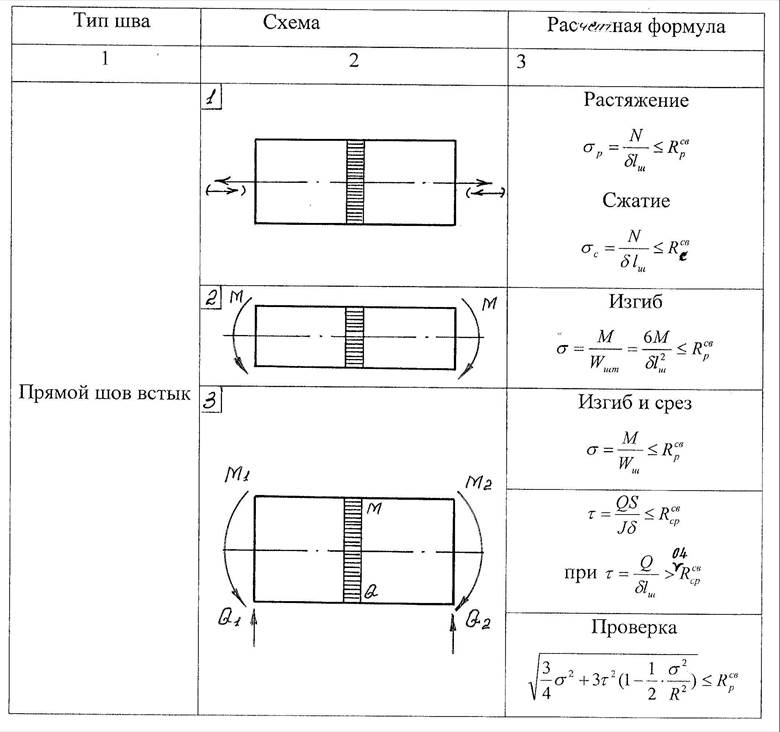 Это осуществляется при помощи специальных интерполяционных вставок между узлами тела болта и узлами краёв отверстий. Отверстия под болты по умолчанию назначаются круглыми, но могут быть и овальными – в этом случае болты могут свободно смещаться вдоль длинной стороны, не воспринимая поперечных усилий в этом направлении. После выполнения расчёта в каждом болте отображаются растягивающие и срезающие усилия.
Это осуществляется при помощи специальных интерполяционных вставок между узлами тела болта и узлами краёв отверстий. Отверстия под болты по умолчанию назначаются круглыми, но могут быть и овальными – в этом случае болты могут свободно смещаться вдоль длинной стороны, не воспринимая поперечных усилий в этом направлении. После выполнения расчёта в каждом болте отображаются растягивающие и срезающие усилия.